一种在线自学习的软测量模型建模方法.pdf

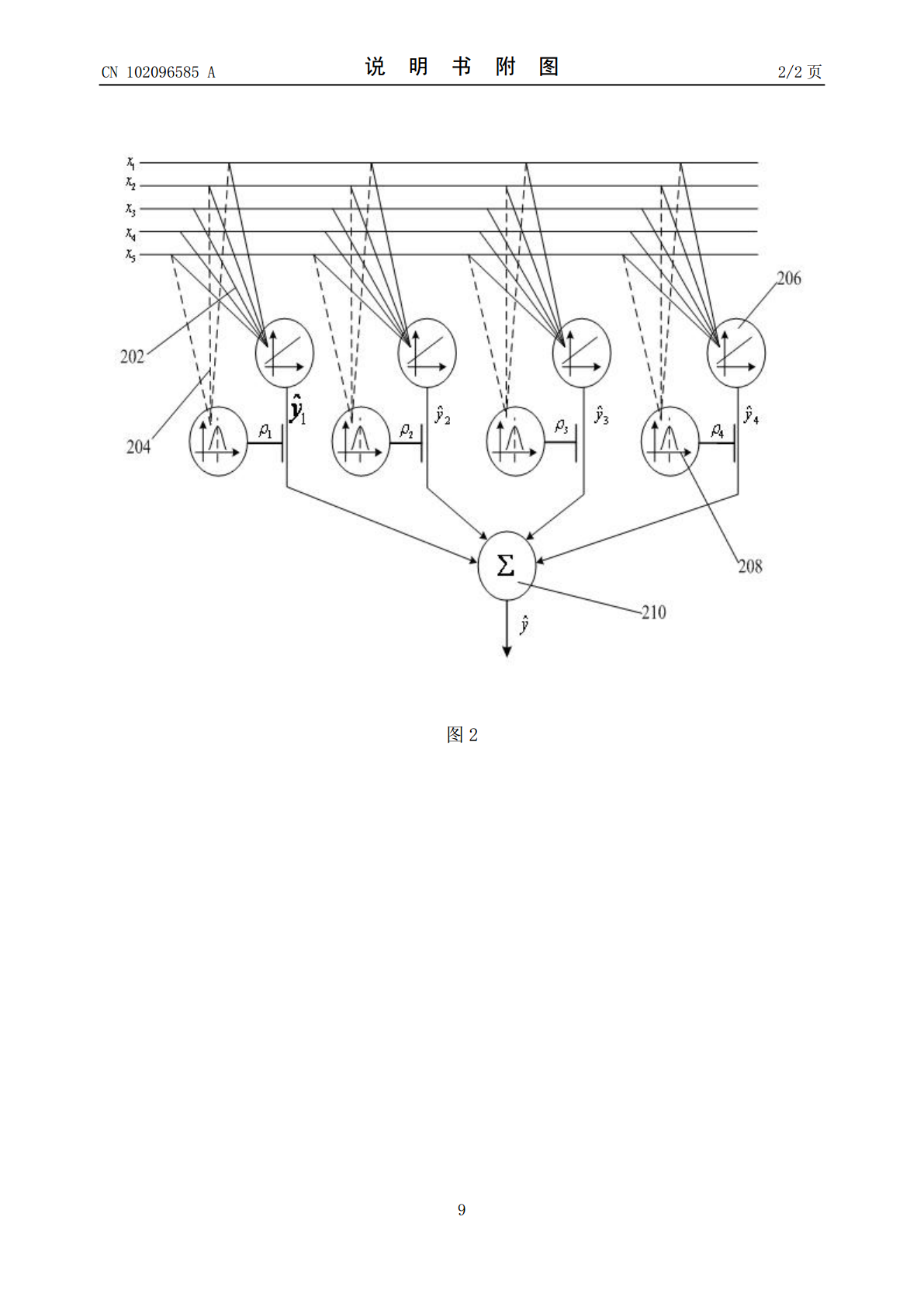
(19)中华人民共和国国家知识产权局*CN102096585A*(12)发明专利申请(10)申请公布号CN102096585A(43)申请公布日2011.06.15(21)申请号201010586539.1(22)申请日2010.12.14(71)申请人江苏大学地址212013江苏省镇江市京口区学府路301号(72)发明人潘天红李正明(74)专利代理机构南京经纬专利商标代理有限公司32200代理人楼高潮(51)Int.Cl.G06F9/44(2006.01)权利要求书2页说明书4页附图2页(54)发明名称一种在线自学习的软测量模型建模方法(57)摘要本发明公开一种在线自学习的软测量模型建模方法，先读取生产过程的在线数据，对其预处理和标准化构造后构造一输入变量集合的输入向量和一输入变量的子集合的调度向量；再用一调度向量在线将系统数据分割为多个局部区域，各局部区域用一输入向量架构一局部线性模型；利用在线减法聚类算法计算一调度向量的密度函数的值；利用增加、更新与合并三个准则来更新已存在的局部区域、产生新的局部区域、或合并最相邻的局部区域，最后由权重值组合各个局部线性模型构建一软测量模型并得出预测输出值。整个过程无需保留系统历史数据，加强了预测输出的准确度并降低系统的在线计算量，能在线捕获系统工况变化，提高模型的自适应能力。CN1029658ACCNN110209658502096594A权利要求书1/2页1.一种在线自学习的软测量模型建模方法，其特征是包括下列步骤：1）读取生产过程的在线数据，对其预处理和标准化构造后构造一输入变量集合的输入向量（202）和一输入变量（202）的子集合的调度向量（204）；2）用一调度向量（204）在线将系统数据分割为多个局部区域，各局部区域用一输入向量（202）架构一局部线性模型（206）；利用在线减法聚类算法计算一调度向量（204）的密度函数（208）的值；3）将该密度函数（208）的值与增加聚类规则作比较，判断是否需要增加新的一局部区域；若是，则以一调度变量（204）为该局部区域的聚类中心计算一输入向量（202）所对应的共变异矩阵；若否，则利用一调度向量（204）更新与调度向量（204）最相邻局部区域的聚类中心，以一输入向量（202）更新其对应的共变异矩阵；4）一输入向量（202）以递归最小二乘方法更新一当前局部区域的局部线性推理模型（206）；5）利用合并局部区域规则判别最相邻的二个局部区域是否可合并成新的一局部区域；若是，则计算合并后一局部区域的聚类中心与其对应的共变异矩阵，并更新合并后一局部区域所对应的局部线性模型系数；6）由权重值组合各个局部线性模型（206），构建一软测量模型（210）并得出预测输出值。2.根据权利要求1所述的一种在线自学习的软测量模型建模方法，其特征是：步骤2）所述的密度函数208的值是：；是调度向量，为时间间隔，，，。3.根据权利要求1所述的一种在线自学习的软测量模型建模方法，其特征是：步骤3）所述的增加聚类规则是若当前的调度向量（204）与已存在的局部区域的聚类中心距离足够远，且当前调度向量（204）的密度函数（208）的值高于已存在的局部区域的密度函数值时，则视为有新的局部区域出现。4.根据权利要求1所述的一种在线自学习的软测量模型建模方法，其特征是：步骤5）所述的合并局部区域规则是：若两局部区域的聚类中心距离够接近到小于合并临界值，则两局部区域将被合并。5.根据权利要求1所述的一种在线自学习的软测量模型建模方法，其特征是：步骤5）所述的局部线性模型（206）定义公式是：；为第局部线性模型（206）2CCNN110209658502096594A权利要求书2/2页的中心位置。6.根据权利要求1所述的一种在线自学习的软测量模型建模方法，其特征是：步骤6）所述的权重值wi是各聚类中心与当前调度向量（204）的距离：；所述的预测输出值由软测量模型（210）由下式估计：。3CCNN110209658502096594A说明书1/4页一种在线自学习的软测量模型建模方法技术领域[0001]本发明涉及一种具有自学习功能的软测量模型建立方法，特别是关于一种利用聚类算法在线捕获系统的工况变化，用于化工过程，属于化工自动化技术领域。背景技术[0002]软件量模型是一种推理模型，使用软件技术来估计生产过程的产品质量。推理模型的建立可以利用不同的数据处理方法，例如：主元回归、偏最小二乘法、人工神经网络、支持向量机、模糊神经系统等等。一般来说，所有的这些推理模型均利用从生产过程中所收集的数据，在离线的情况下建立的。然而，在实际情况下，用于建模的数据并不能覆盖系统所有的实际工况，当有新的工况出现时，就需要重新建立系统的软测量模型。递归主元回归、递推偏最小二乘方法、基于滚动窗口的自适应主元回