差错控制编码课.ppt

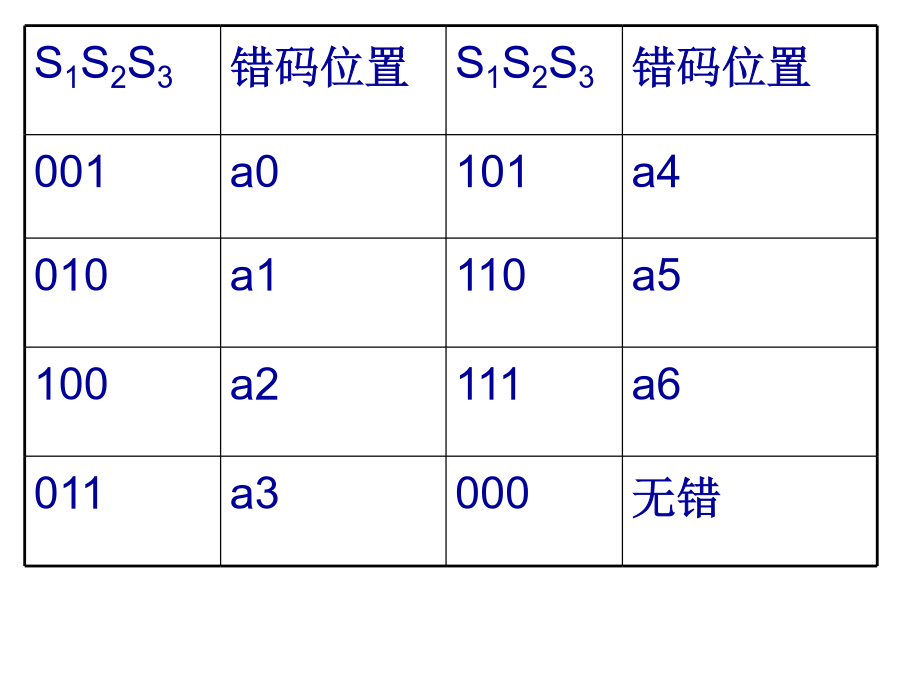
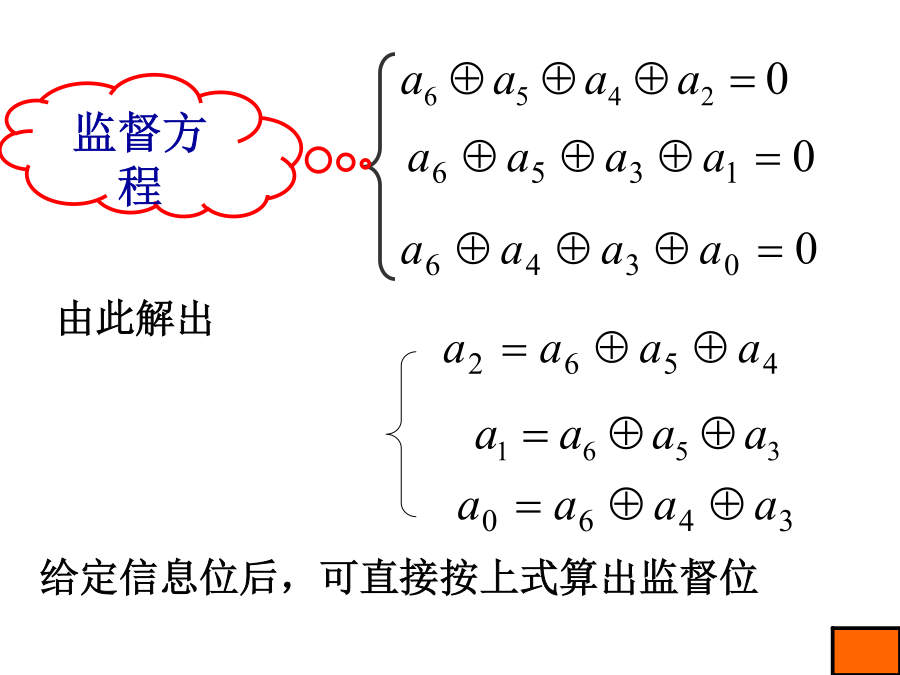
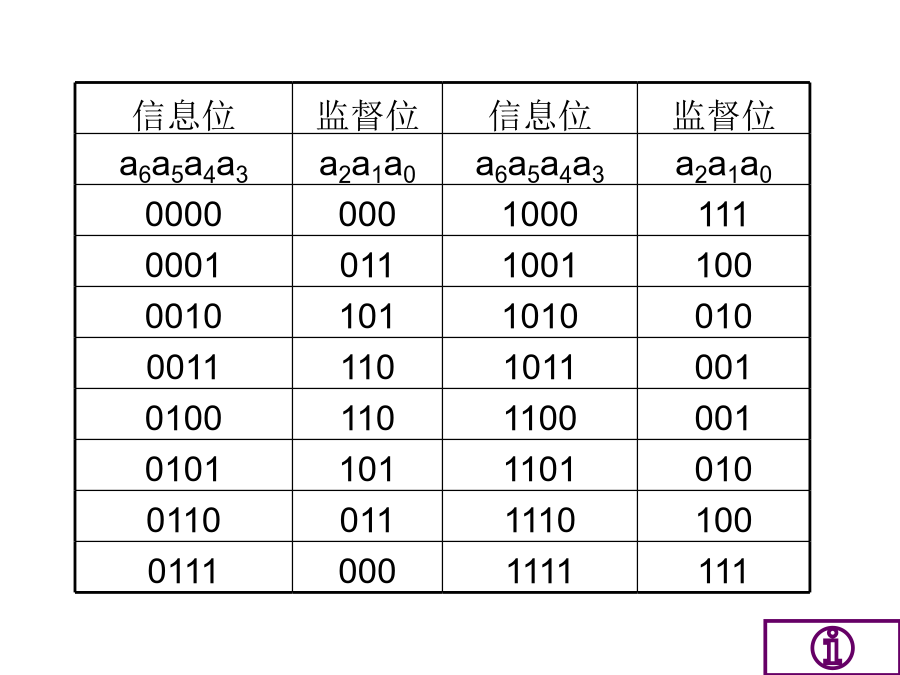
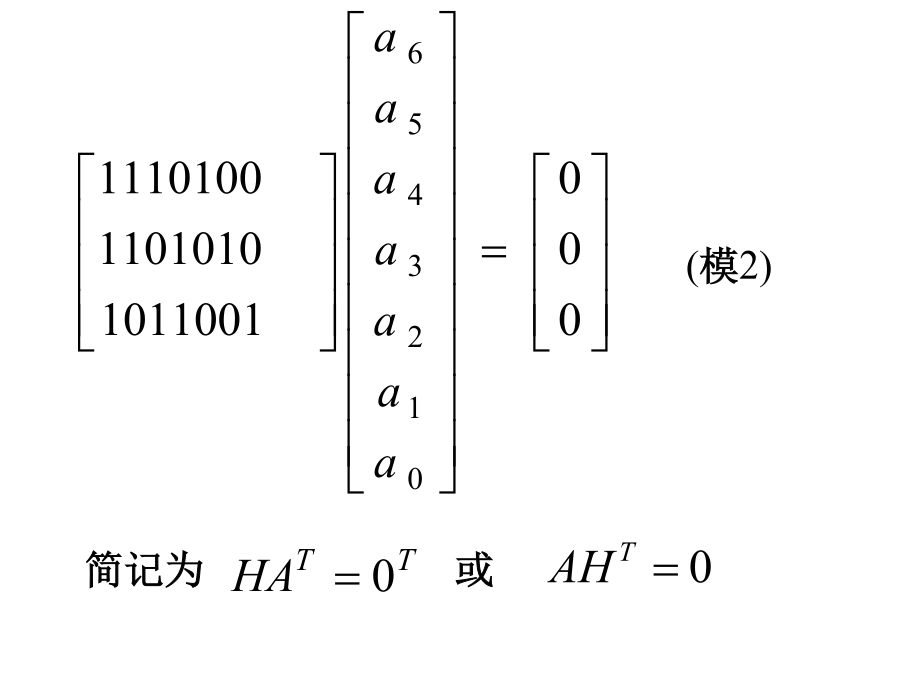
11.5线性分组码回顾奇偶监督码在（n,k）码中，为能纠正一位错误要求举例说明如何构造监督关系式：
上例中，若取r=3，则n=k+r=7。
(7,4)线性分组码（a6a5a4a3a2a1a0)
校正子与错码位置的对应关系如表规定(也可以另外规定)。S1S2S3由表可见，当一错码位置在a2,a4，a5或a6时校正子S1为1；否则S1为0即构成如下关系由此解出信息位2、监督矩阵H和生成矩阵G(模2)称为监督矩阵转置得Q=PT，在Q矩阵的左边在加上一个k×k的单位矩阵，就形成了一个新矩阵G：G为典型生成矩阵，则得到的码为系统码
否则得到的码为非系统码例【1】已知线性（6，3）码的生成矩阵为例2已知（7，4）码的生成矩阵为：例3课后习题9-6
1、写出监督方程
2、由监督方程求出所有许用码组
3、求生成矩阵
4、最小码距？只用于检错，能检出几位错码？只用于纠错？同时用于检错和纠错？
若发送码组为接收端译码时计算纠错-----------只纠一位错误时例4设解：1）若无错，则错误图样为0，S为0例5、已知一（7，4），监督码元和信息码元之间的关系为：
4、汉明码§9.4线性分组码回顾奇偶监督码在接收端解码时，实际上
就是在计算

若S＝0，认为无错；若S＝1，认为有错。

上式称为监督关系式，S称为校正子。S只
有两种取值，只能代表有、无错两种信
息，不能指出错码位置。

如果监督位增加一位，则增加一个监督关
系式。两个校正子的可能值有4种组
合：00，01，10，11，故能表示4种不同
状态。若用其一种表示无错，则其余3种就可能用来指示一位错码的3种不同位置。同理r个监督关系式能指示一位错码的(2r-1)个可能位置。
一般地，若码长为n，信息位数为k，则监督位数r=n-k。如果希望用r个监督位构造出r个监督关系式来指示一位错码的n种可能位置，则要求
2r-1≥n，或者2r≥r+k+1举例说明如何构造监督关系式：
设(n，k)分组码中k=4。为了纠正一位错码，要求监督位数r≥3。若取r=3，则n=k+r=7。校正子与错码位置的对应关系如表9—4规定(也可以另外规定)。由表可见，当一错码在a2,a4，a5或a6时校正子S1为1；否则S1为0.
a2,a4，a5和a6构成偶数监督关系。
即构成如下关系:
同理
由此解出信息位接收端收到每个码组后，先按监督方程计算出S1、S2、S3，再按表9—4判断错码情况。例：接收0000011，可得：
S1S2S3=011。由表9—4可知在a3位有错码。
(7，4)汉明码：
最小码距d0=3
纠一个错码或检测两个错码。
编码效率k/n=(2r-1-r)／(2r-1)=I-r／n。当n很大时，则编码效率接近1。线性分组码的—般原理。线性分组码是指信息位和监督位满足一组线性方程的编码。

改写为
(模2)称为监督矩阵转置得称为典型
生成矩阵生成矩阵G的每一行都是一个码组。
例如，（参照前页矩阵G）。
利用生成矩阵，码字译码,若发送码组为

接收码组为

二者之差为

其中E称为错误图样。接收端译码时计算

当接收码组无错时．S等于零
有错但不超过检错能力时，S不等于零。
在错码超过检错能力时，B变为另一许用码组，仍能成立S等于零。这样的错码是不可检测的。
S称为校正子(伴随式)。S只与E有关，而与A无关，意味着S与E有的线性变换关系，能与E一一对应，可指示错码位置。线性码重要性质之一，是它具有封闭性。
若：A1和A2是线性码中的两个许用码组，则：(A1+A2)仍为其中的一个码组。
由封闭性，两个码组之间的距离必是另一码组的重量。故码的最小距离即是码的最小重量(除全“0”码组外)。
线性码又称群码，这是由于线性码的各许用码组构成代数学中的群。9.3.4线性分组码的译码
码字Ci接收字RCi的估值

干扰
1.差错图案
线性分组码C的任一码字Ci=(ci1,ci2,…,cin)经信道
传输后，接收到字R=(r1,r2,…,rn)；令
E=R-Ci=(r1-ci1,r2-ci2,…,rn-cin);
这里称E为差错图案。根据模2运算的性质，E=R+Ci
E=0则R是码C的码字；否则，R不是码C的码字。
对于二元(n,k)码，差错图案E的分量中“1”的个数即
为接收码字R差错的个数。
差错图案出现t个差错的图案数量为Cnt。2.伴随式
根据CiHT=01×(n-k)及R=Ci+E，

RHT=(Ci+E)HT=CiHT+EHT=EHT

令S=RHT或S=EHT;这里S=(s1,s2,…,sn-k)
这里称S为伴随式。

伴随式S仅与接收字R或差错图案E有关，与码字Ci
无关。
由于伴随式S是n-k维矢量，故不同S的个数只有2n-k
个；而接收字R或差错图案E有2n个，因此，不同的接收
字R或差错图案E有相同