
大数定律与中心极限定理 (2).ppt

YY****。。








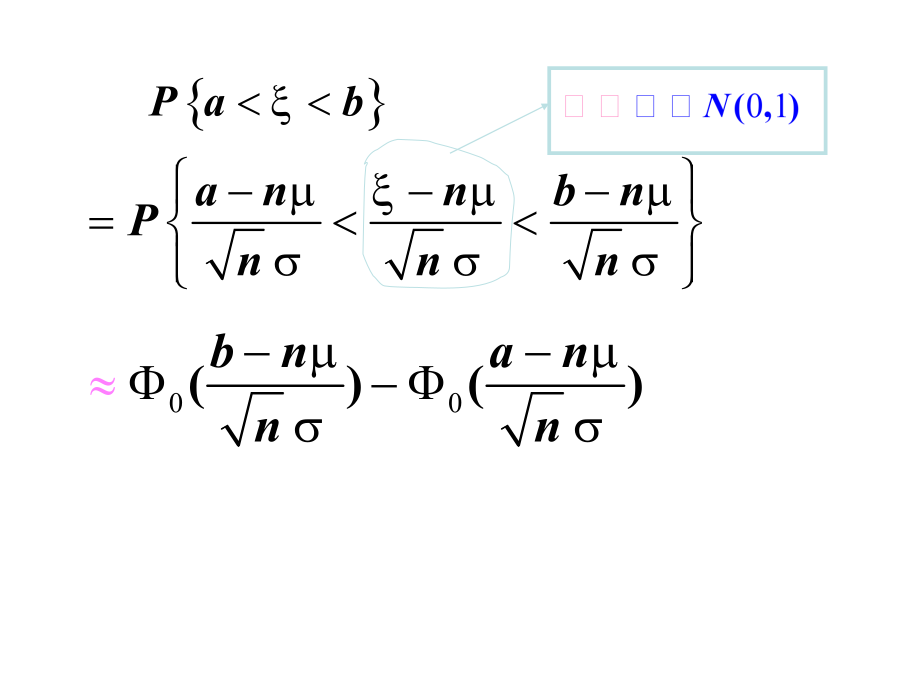
亲,该文档总共22页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

大数定律与中心极限定理 (2).ppt
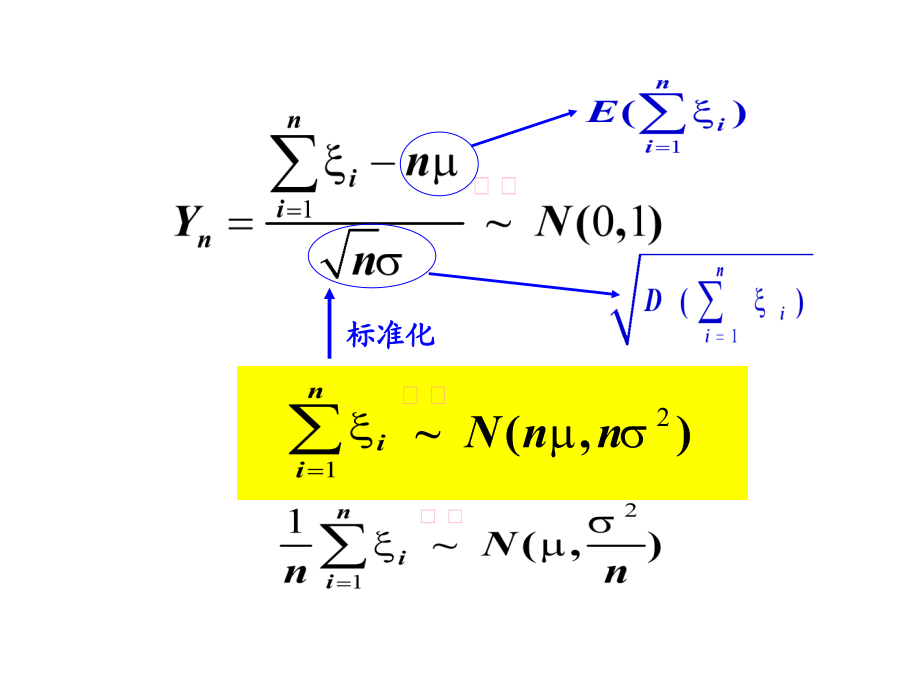
§35大数定律与中心极限定理一、依概率收敛二、大数定律定理39(切比雪夫大数定律)设12n是一列两两不相关的随机变量它们的数学期望Ei和方差Di均存在且方差有界即存在常数C使得DiC(i12)则对任意0有定理310(辛钦大数定律)设12n是一列相互独立同分布的随机变量且数学期望存在记Ei则有要解决的问题:记标准化注:例330一盒同型号螺丝钉共有100个已知该型号的螺丝钉的重量是一个随机变量期望值是

大数定律和中心极限定理(2).ppt
概率论(续)第五章大数定律和中心极限定理§1大数定律4例1:在n重贝努里试验中,若已知每次试验事件A出现的概率为0.75,试利用契比雪夫不等式,(1)若n=7500,估计A出现的频率在0.74至0.76之间的概率至少有多大;(2)估计n,使A出现的频率在0.74至0.76之间的概率不小于0.90。随机变量序列依概率收敛的定义7契比雪夫大数定律表明,当n很大时,的算术平均接近于数学期望。这种接近是在概率意义下的接近。例2:大数定律的重要意义:贝努里大数定律建立了在大量重复独立试验中事件出现频率的稳定性,正因

大数定律和中心极限定理 (2).ppt
第五章大数定律和中心极限定理第一节大数定律由车贝雪夫不等式得:此定理说明了频率的稳定性。由数学期望和方差的性质第二节中心极限定理独立地掷10颗骰子,求掷出的点数之和在30到40点之间的概率.在一家保险公司有一万人参加保险,每年每人付12元保险费.在一年内这些人死亡的概率都为0.006,死亡后家属可向保险公司领取1000元,试求:(1)保险公司一年的利润不少于6万元的概率;(2)保险公司亏本的概率。公司一年的利润为:(1)保险公司一年的利润不少于6万元的概率为独立地测量一个物理量,每次测量产生的误差都服从区

大数定律及中心极限定理.doc
第五章大数定律及中心极限定理出题人:蒲兴成基本要求理解大数定律及中心极限定理的内涵;熟记大数定律及中心极限定理的几种基本形式;能够指出大数定律及中心极限定理成立时应满足的条件;能用大数定律及中心极限定理解决一些实际问题.部分习题讲解1.根据以往经验,某种元件的寿命服从均值为100小时的指数分布,现随机地取16只,设它们的寿命是相互独立的.求这16只元件的寿命的总和大于1920小时的概率.解:以表示第只电器的使用寿命,则记,即表示这16只电器的使用寿命之和,据独立同分布的中心极限定理有:2.一部件包括10部

大数定律及中心极限定理.pptx
第五章大数定律及中心极限定理概率论与数理统计是研究随机现象统计规律性旳学科。而随机现象旳统计规律性是在相同条件下进行大量反复试验呈现出来旳。例如,在概率旳统计定义中,曾提到一事件发生旳频率具有稳定性,即事件发生旳频率趋于事件发生旳概率:当试验次数无限增大时,事件发生旳频率在某种收敛意义下逼近一定数。这就是最早旳大数定律。一般旳大数定理讨论n个随机变量旳平均值旳稳定性。定理1(切比雪夫定理旳特殊情况)设随机变量序列X1,X2,…,Xn,...相互独立,且具有相同旳数学期望和方差:证定理2(贝努力大数定律)设
