大数定律和中心极限定理 (2)-豆柴文库

大数定律和中心极限定理 (2).ppt

2024-09-10

16金币

1.1MB

24页

sy****28

实名认证

内容提供者

1/10

2/10

3/10

4/10

5/10

6/10

7/10

8/10

9/10

10/10

亲，该文档总共24页，到这已经超出免费预览范围，如果喜欢就直接下载吧～

下载提示文本预览

如果您无法下载资料，请参考说明：

1、部分资料下载需要金币，请确保您的账户上有足够的金币

2、已购买过的文档，再次下载不重复扣费

3、资料包下载后请先用软件解压，在使用对应软件打开

相关资料

大数定律和中心极限定理(2).ppt

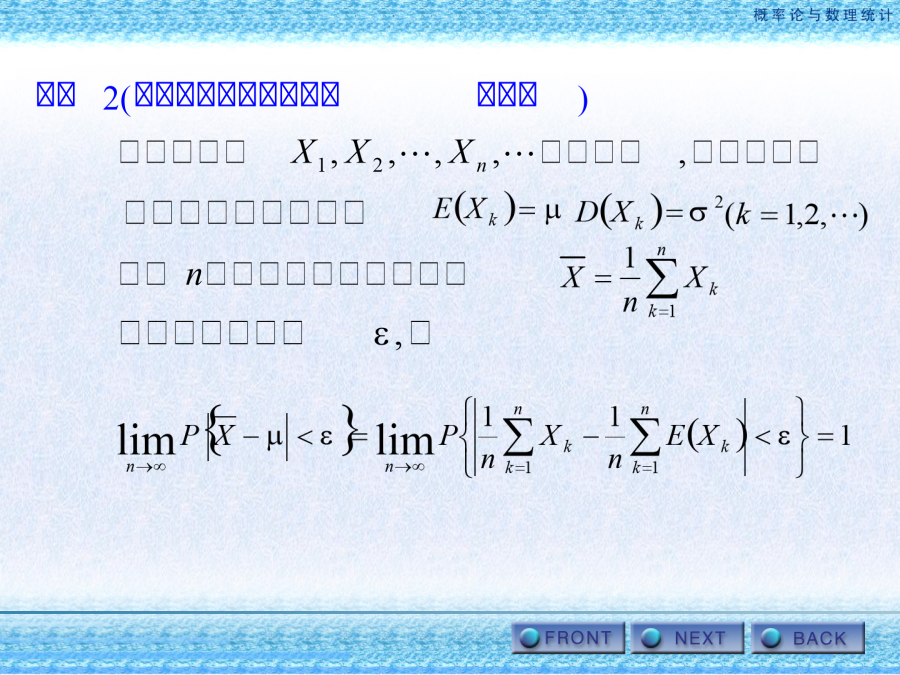
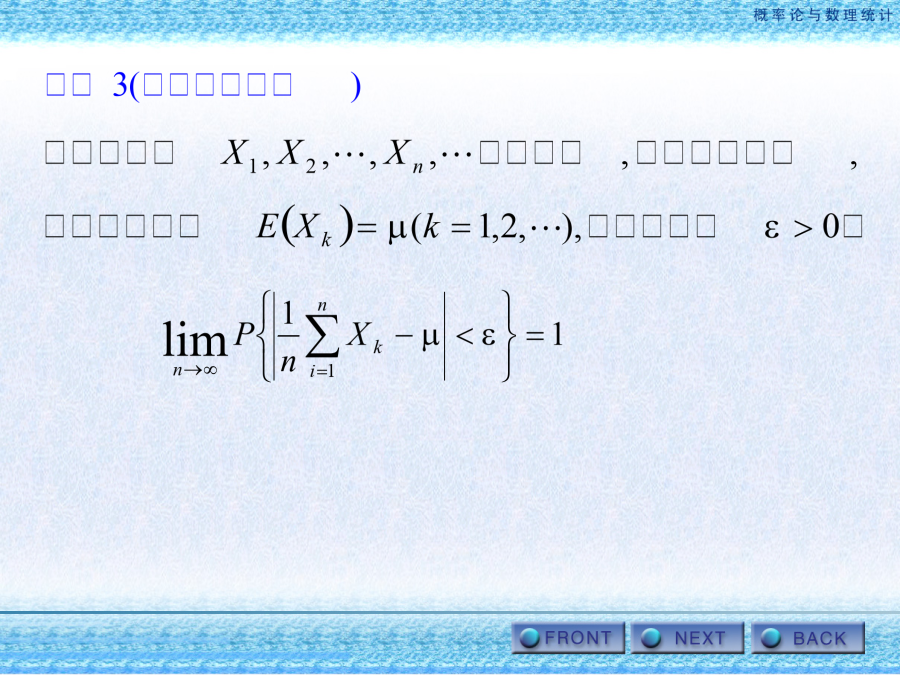
概率论(续）第五章大数定律和中心极限定理§1大数定律4例1：在n重贝努里试验中，若已知每次试验事件A出现的概率为0.75，试利用契比雪夫不等式,(1)若n=7500,估计A出现的频率在0.74至0.76之间的概率至少有多大；（2）估计n,使A出现的频率在0.74至0.76之间的概率不小于0.90。随机变量序列依概率收敛的定义7契比雪夫大数定律表明，当n很大时，的算术平均接近于数学期望。这种接近是在概率意义下的接近。例2：大数定律的重要意义：贝努里大数定律建立了在大量重复独立试验中事件出现频率的稳定性，正因

2024-09-02

2.4MB

大数定律和中心极限定理 (2).ppt

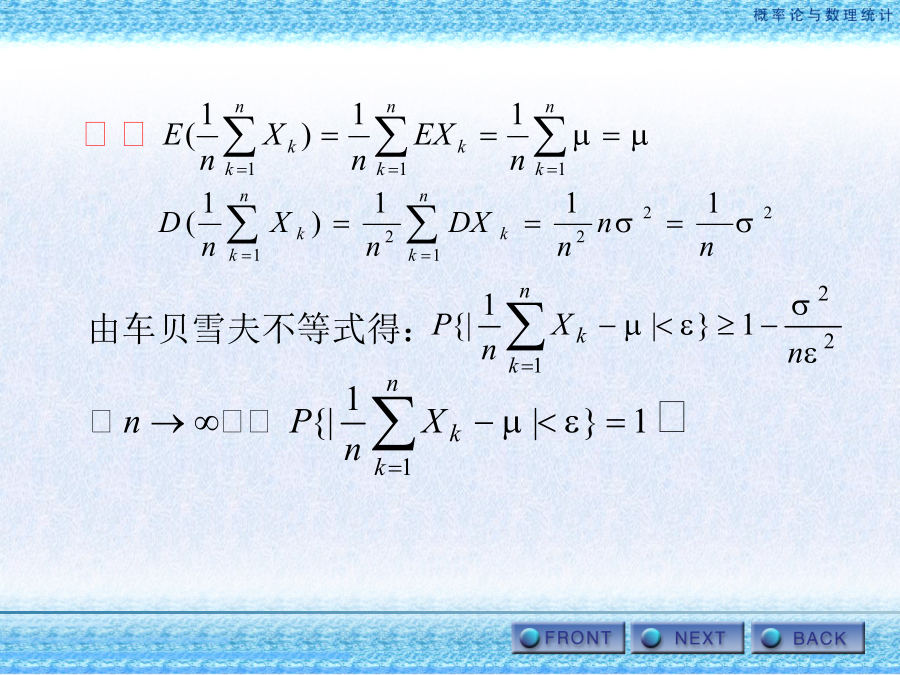
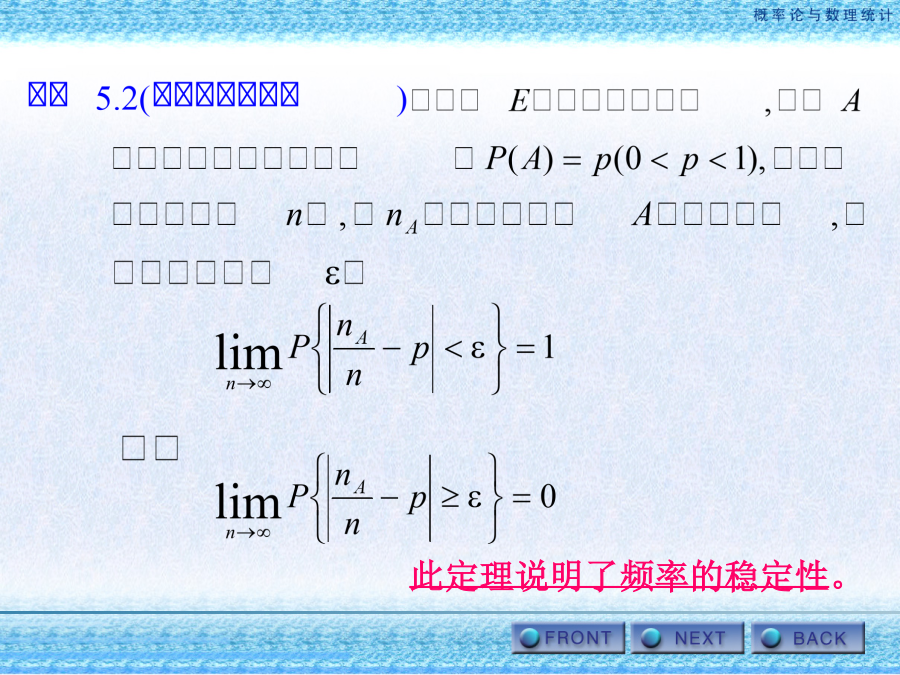
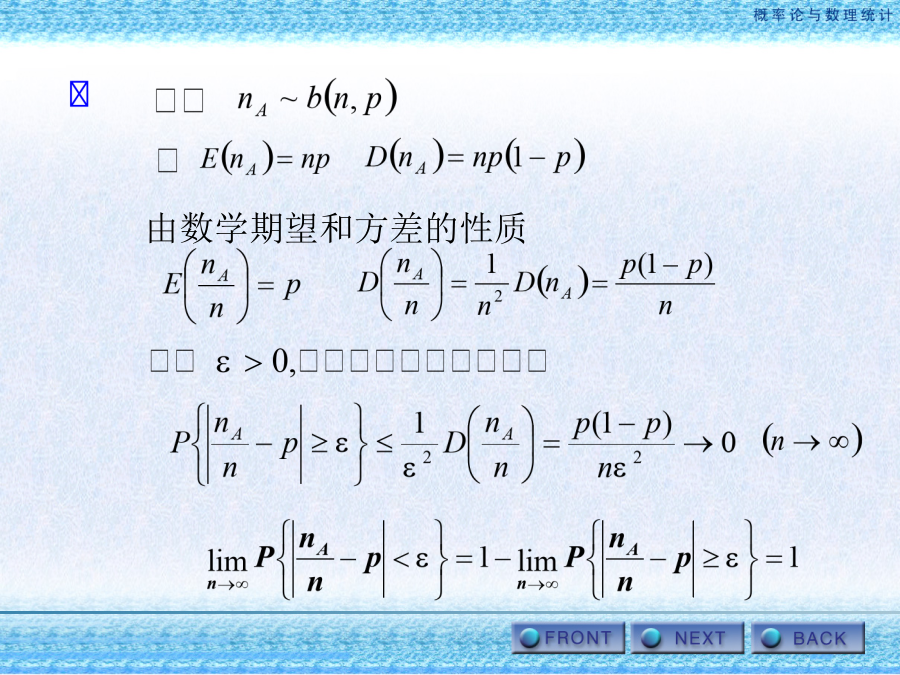
第五章大数定律和中心极限定理第一节大数定律由车贝雪夫不等式得：此定理说明了频率的稳定性。由数学期望和方差的性质第二节中心极限定理独立地掷10颗骰子，求掷出的点数之和在30到40点之间的概率．在一家保险公司有一万人参加保险，每年每人付12元保险费．在一年内这些人死亡的概率都为0.006，死亡后家属可向保险公司领取1000元，试求：（1）保险公司一年的利润不少于6万元的概率；（2）保险公司亏本的概率。公司一年的利润为：(1)保险公司一年的利润不少于6万元的概率为独立地测量一个物理量，每次测量产生的误差都服从区

2024-09-10

1.1MB

大数定律和中心极限定理.docx

第五章大数定律和中心极限定理总述内容提要本章主要讲述契比雪夫不等式，契比雪夫大数定律，贝努里大数定律和中心极限定理等内容．重点分析了解切比雪夫不等式、切比雪夫定理和伯努利定理。了解独立同分布的中心极限定理和棣莫佛—拉普拉斯定理。难点分析切比雪夫定理。独立同分布的中心极限定理。习题布置习题5备注第17次教案§5.1大数定律人们在长期的实践中发现，事件发生的频率具有稳定性，也就是说随着试验次数的增多，事件发生的频率将稳定与一个确定的常数。对某个随机变量进行大量的重复观测，所得到的大批观测数据的算术平均值也具有

2024-11-06

135KB

大数定律和中心极限定理.docx

第五章大数定律和中心极限定理一、内容提要（一）切贝谢夫不等式1.切贝谢夫不等式的内容设随机变量X具有有限的数学期望E（X）和方差D（X），则对任何正数ε，下列不等式成立。2.切贝谢夫不等式的意义（1）只要知道随机变量X的数学期望和方差（不须知道分布律），利用切贝谢夫不等式，就能够对事件的概率做出估计，这是它的最大优点，今后在理论推导及实际应用中都常用到切贝谢夫不等式。（2）不足之处为要计算的值时，切贝谢夫不等式就无能为力，只有知道分布密度或分布函数才能解决。另外，利用本不等式估值时精确性也不够。（3）当X

2024-11-07

167KB

大数定律和中心极限定理.ppt

1不等式的说明例1：n重贝努里试验中，已知每次试验事件A出现的概率为0.75，试利用契比雪夫不等式,(1)若n=7500,估计A出现的频率在0.74至0.76之间的概率至少有多大；（2）估计n,使A出现的频率在0.74至0.76之间的概率不小于0.90。随机变量序列依概率收敛的定义5大数定律的重要意义：贝努里大数定律建立了在大量重复独立试验中事件出现频率的稳定性，正因为这种稳定性，概率的概念才有客观意义，贝努里大数定律还提供了通过试验来确定事件概率的方法，既然频率nA/n与概率p有较大偏差的可能性很小，我

2024-06-30

463KB