内容提供者
垂直于弦的直径公开课版.ppt
2024-11-26
10金币
738KB
11页
YY****。。
实名认证
内容提供者
1/10
2/10
3/10
4/10
5/10
6/10
7/10
8/10
9/10
10/10
亲，该文档总共11页，到这已经超出免费预览范围，如果喜欢就直接下载吧～
相关资料
垂直于弦的直径公开课版.ppt
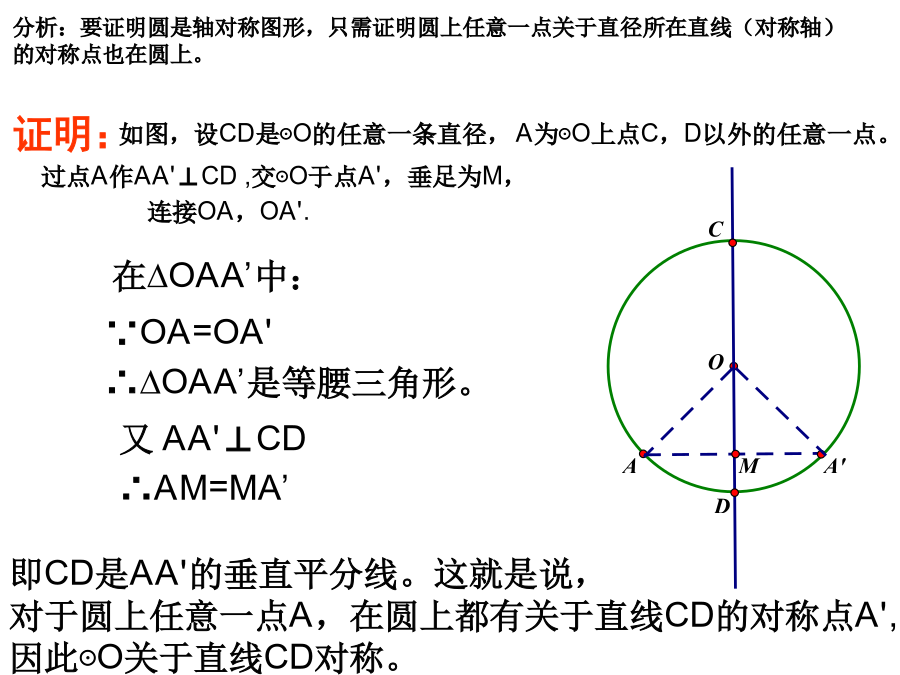
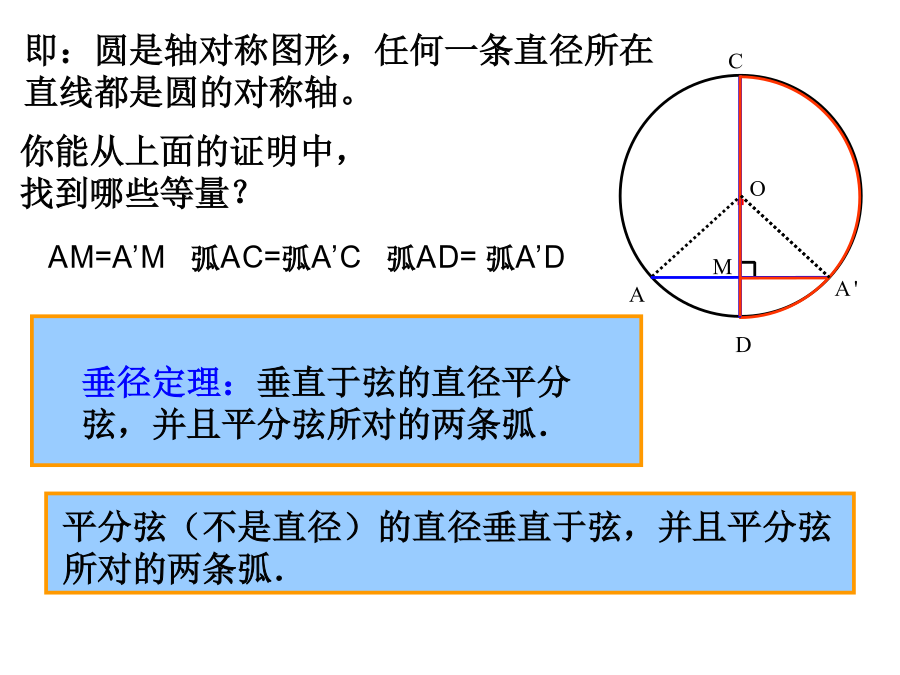
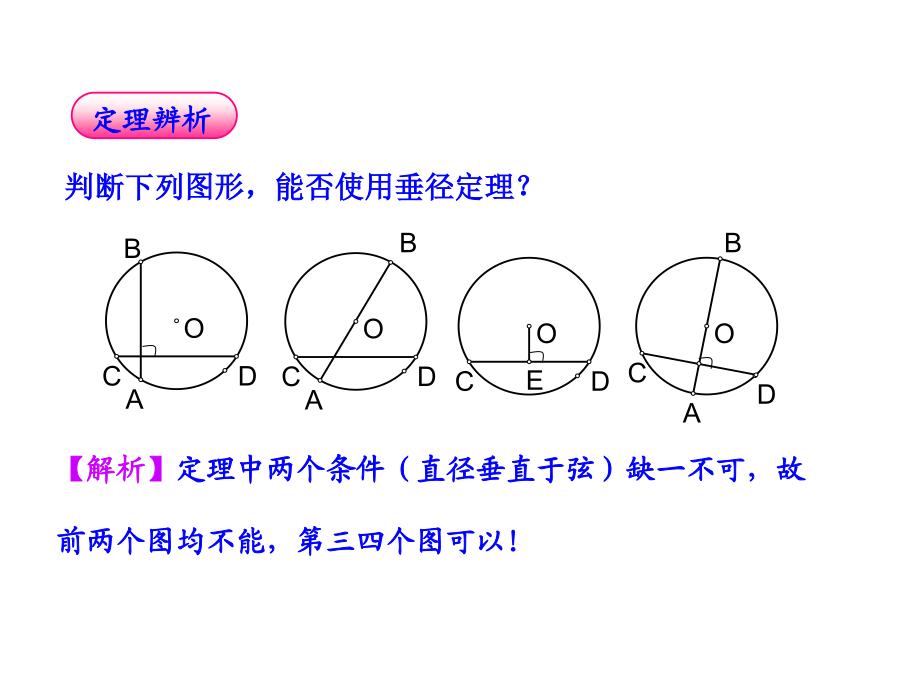
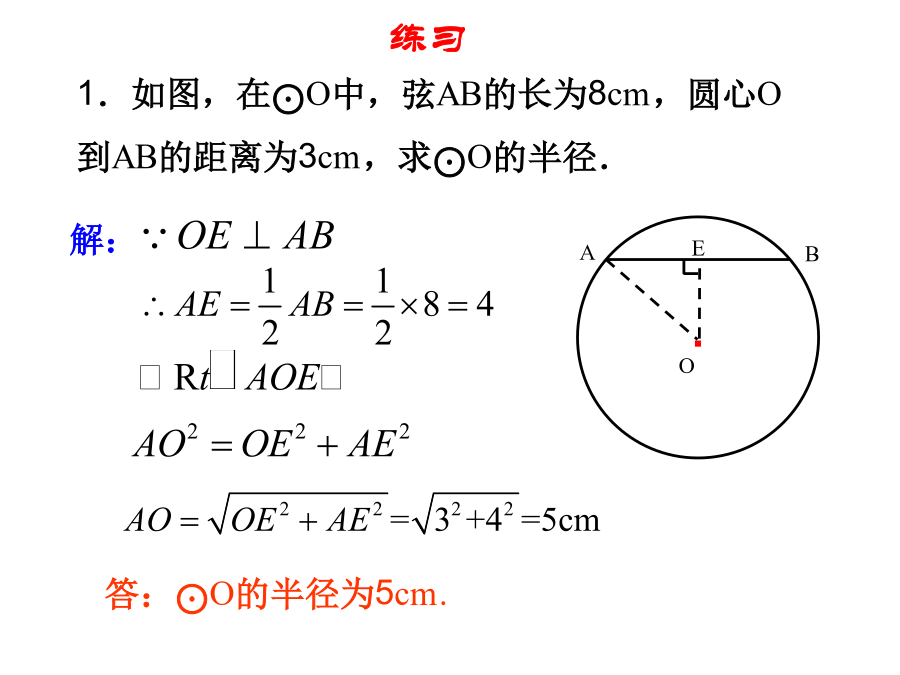
24.1.2垂直于弦的直径问题：赵州桥是我国隋代建造的石拱桥，距今约有1400年的历史，是我国古代人民勤劳与智慧的结晶．它的主桥拱是圆弧形，它的跨度(弧所对的弦的长)为37m，拱高(弧的中点到弦的距离)为7.23m，求赵州桥主桥拱的半径（结果保留小数点后一位）．证明：·判断下列图形，能否使用垂径定理？1．如图，在⊙O中，弦AB的长为8cm，圆心O到AB的距离为3cm，求⊙O的半径．例2赵州桥是我国隋代建造的石拱桥，距今约有1400年的历史，是我国古代人民勤劳与智慧的结晶．它的主桥拱是圆弧形，它的跨度(弧所
2024-11-26
10
738KB
垂直于弦的直径.1.2垂直于弦的直径.pptx
问题：你知道赵州桥吗?它是1300多年前我国隋代建造的石拱桥(如图),是我国古代人民勤劳与智慧的结晶．它的主桥是圆弧形,它的跨度(弧所对的弦的长)为37.4m,拱高(弧的中点到弦的距离)为7.2m.24.1.2垂直于弦的直径【学习目标】1．探索并了解圆的对称性和垂径定理．2．能运用垂径定理解决几何证明、计算问题，并会解决一些实际问题．【学习重点】垂径定理、推论及其应用．【学习难点】发现并证明垂径定理．直径ＣＤ平分弦ＡＢ，并且平分ＡＢ及ＡＣＢ垂径定理三种语言③AM=BM,判断下列说法的正误解得：R≈27．9
2024-09-27
15
387KB
垂直于弦的直径.1 垂直于弦的直径.ppt
24.1圆的有关性质（第2课时）学习目标：1．通过观察实验，理解圆的轴对称性；2．掌握垂径定理，理解其证明，并会用它解决有关的证明和计算问题；3．经历探究过程，体会和理解研究几何图形的各种方法．学习重难点：垂径定理及其应用．如图，1400多年前，我国隋代建造的赵州石拱桥主桥拱是圆弧形，它的跨度（弧所对的弦长）是37m，拱高（弧的中点到弦的距离）为7.23m，求赵州桥主桥拱的半径（精确到0.1m）．请拿出准备好的圆形纸片，沿着它的直径翻折，重复做几次，你发现了什么？由此你能得出什么结论？2．探究新知已知：如
2024-09-25
16
1.1MB
垂直于弦的直径.1.2垂直于弦的直径.doc
临江新区实验初中海门市临江新区实验初中集体备课教案初三教研组主备者朱海玲年月日教学内容（章节、课文）垂径定理共几课时2课型新第几课时1教学目标理解圆的对称性，掌握垂径定理及其他结论，并学会用这些结论解决一些有关证明、计算和作图问题。进一步发培养学生的合情推理能力，发展学生的逻辑思维能力和推理论证的表达能力。教学重点、难点1．重点：垂径定理的理解与应用2．难点：掌握垂径定理．教学资源直尺、圆规、刻度尺、预习设计1.画圆，并折叠，体会圆的对称性2.课前思考：如何求圆弧形拱桥的半径？学程预设导学策略调整与反思一
2024-09-26
16
219KB
垂直于直径的弦.1.2 垂直于弦的直径.ppt
③AE=BE,你可以写出相应的命题吗?（小组讨论）条件②CD⊥AB,挑战自我填一填例1.在圆O中，AB不平行CD，M,N分别为AB，CD中点，AB=CD，求证：∠AMN=∠CNM.例2.如图：A,B,C为圆O上三点，D为弧AB的中点，E为弧AC的中点，连接DE分别交AB、AC于F、G.求证：AF=AG.课堂小结
2024-09-25
16
490KB