
垂径定理说课.ppt

YY****。。







亲,该文档总共11页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

垂径定理说课.ppt
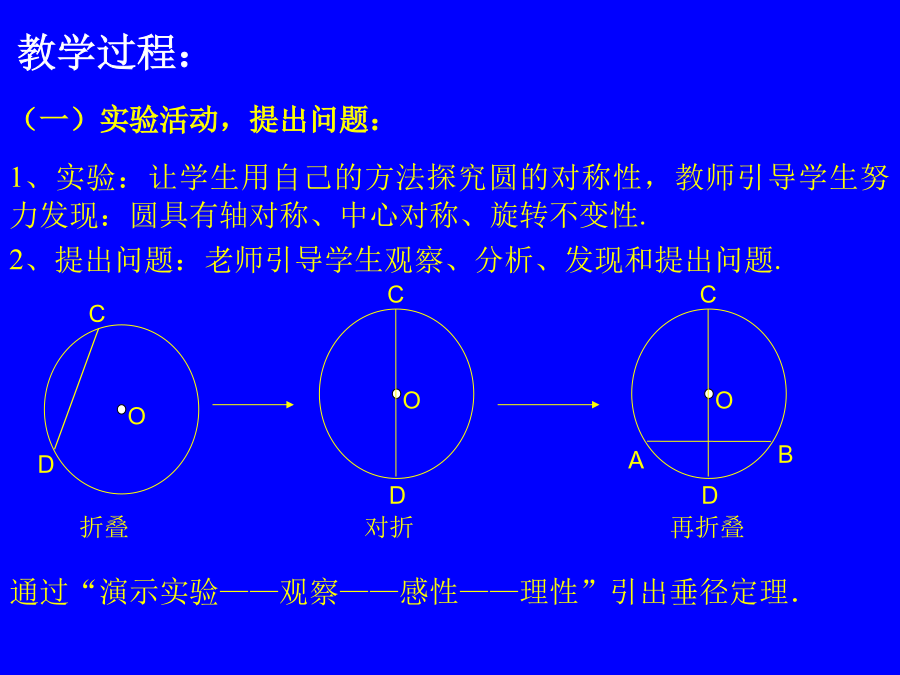
24.1.2垂直于弦的直径说课24.1.2垂直于弦的直径教材分析各位领导,老师你们好!今天我要为大家讲的课题人教版九年级(上)第二十四章第二节,《垂直于弦的直径》的第一课时。首先,我对本节教材进行一些分析:人教版《数学》九年级(上)第24章“24.2垂径定理”二、学生情况分析三、教学目标四、教法与学法五、教学过程1.创设情景,激发兴趣利用实践得出定理如图,AB是⊙O的一条弦,做直径CD,使CD⊥AB,垂足为E.(1)圆是轴对称图形吗?如果是,它的对称轴是什么?(2)你能发现图中有那些相等的线段和弧?为什么

垂径定理说课.ppt
第三章圆教材分析1、教材所处的地位以及前后联系:这节课的主要内容是垂径定理及其推论,它们是在学生学习轴对称图形及其性质等知识的基础上学习的,是本章的重点内容之一,也是在中考中常常用到的定理。这个定理提供了证明两条线段相等,两条孤相等,垂直和证明直径的方法。因此,学好本节课的知识尤为重要。可以说这节课无论在知识上,还是在学生能力培养上,都起着十分重要的作用。2、教学目标:1)、知识目标:A、理解掌握圆是一个轴对称图形。B、在清晰垂径定理的题设与结论的基础上,熟记垂径定理及其两个推论。2)、能力目标:能够在有

垂径定理.3.2垂径定理综合课.ppt
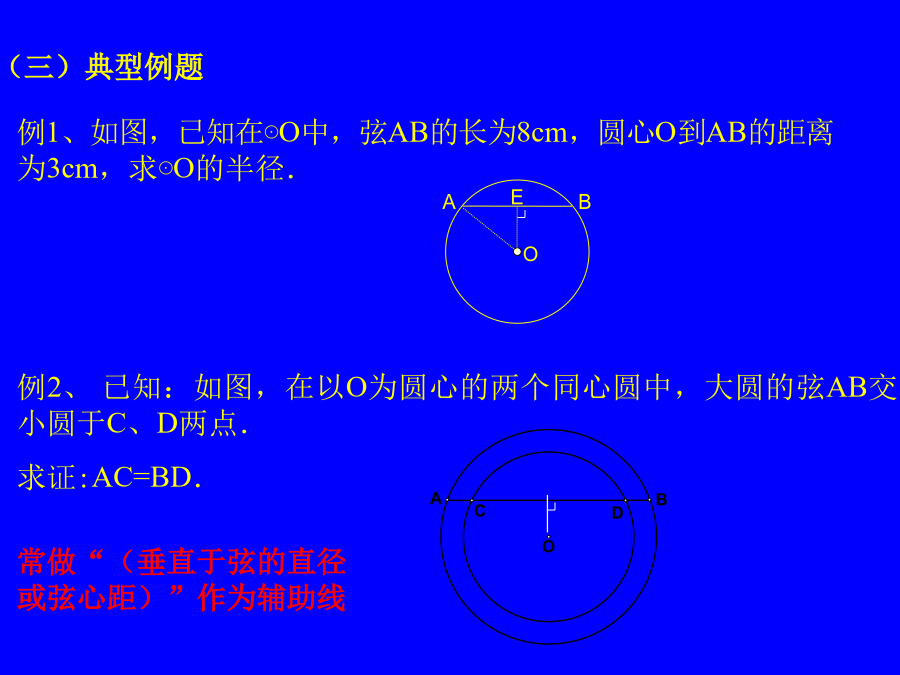
2.3.2垂径定理综合课·应用垂径定理的书写步骤1应用垂径定理的书写步骤2应用垂径定理的书写步骤3判断下列图形,能否使用垂径定理?1.如图,⊙O的半径为5cm,圆心O到弦AB的距离为3cm,求弦AB的长.1.如图,在⊙O中,弦AB的长为8cm,圆心O到AB的距离为3cm,求⊙O的半径.1.如图,⊙O中,弦AB的长为8cm,弓形ADB的高为2cm,求⊙O半径.2、如图4,在⊙O中,AB为⊙O的弦,C、D是直线AB上两点,且0C=OD.求证:AC=BD3、如图4,在⊙O中,AB为⊙O的弦,C、D是直线AB上两

垂径定理说课课件.ppt
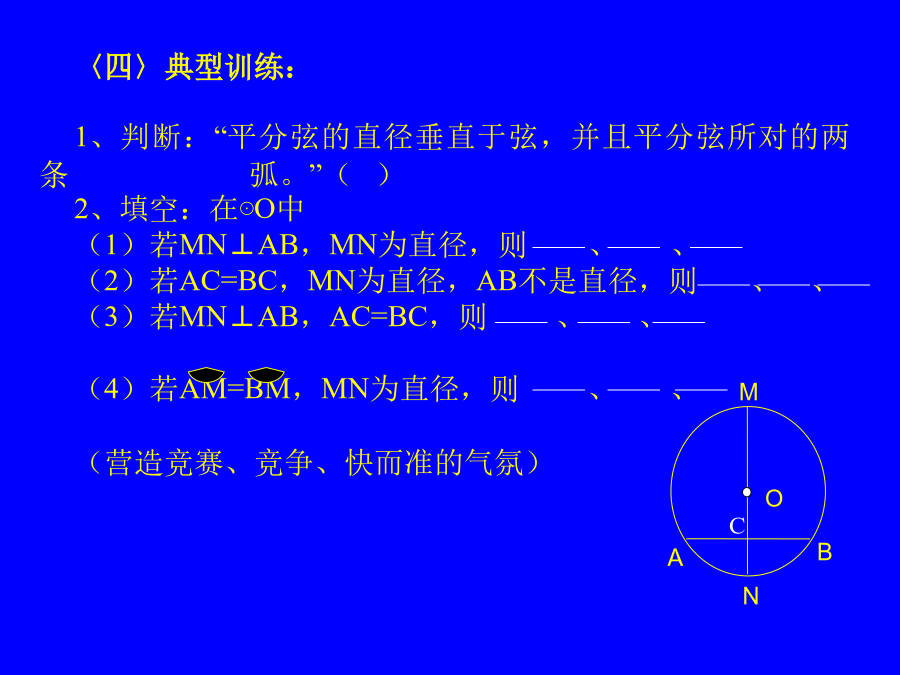
24.1.2垂直于弦的直径我从以下三个方面对本课的设计进行说明:教材的地位和作用教学目标教学重难点教学方法和手段问题:你知道赵州桥吗?它是1300多年前我国隋代建造的石拱桥,是我国古代人民勤劳与智慧的结晶.它的主桥是圆弧形,它的跨度(弧所对的弦的长)为37.4m,拱高(弧的中点到弦的距离)为7.2m,你能求出赵洲桥主桥拱的半径吗?实践探究在自己的圆形纸片中做一条弦AB,再做直径CD,使CD⊥AB,垂足为E.沿CD所在的直线折叠,你能发现图中有那些相等的线段和弧?为什么?③AM=BM,讨论根据垂径定理与推论

垂径定理.1.2 垂径定理.ppt
24.1.2OOO证明结论垂径定理①直线CD过圆心O②CD⊥AB如果交换垂径定理的题设和结论的部分语句,会有一些什么样的结论呢?①直线CD过圆心③AM=BM推论1.(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。O推论1:(2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧;O推论1:(3)平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧。小结判断赵州桥又名安济桥,建于隋大业(公元605-618)年间,距今已1400年,是著名匠师李春建造。主桥拱是圆弧形,跨度(弧所对的弦长3
