优化问题的MATLAB求解.ppt

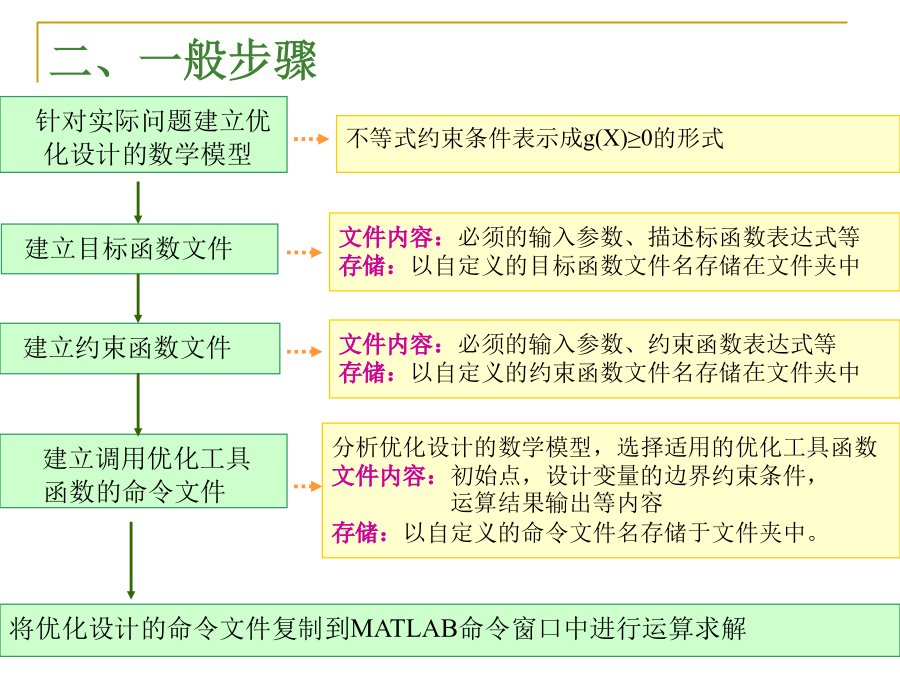
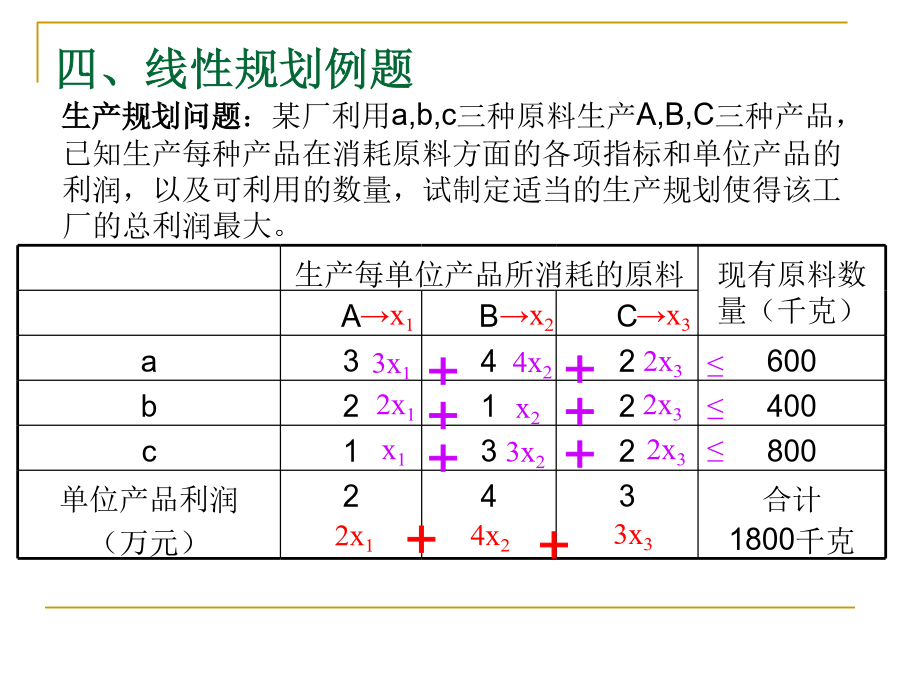
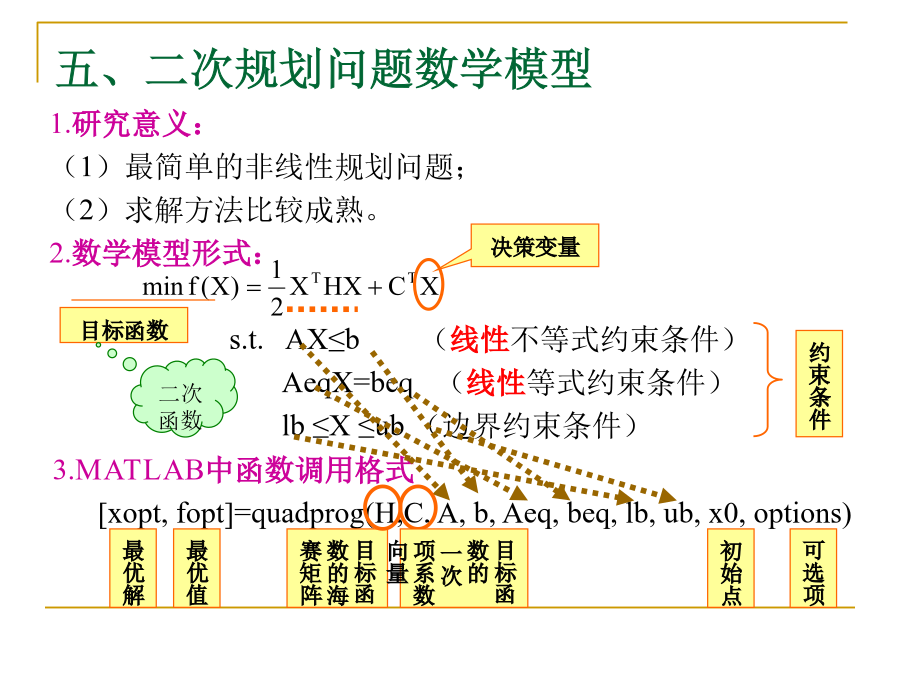
优化问题的MATLAB求解一、matlab优化工具箱中常用的功能函数

求解线性规划问题的主要函数是linprog。
求解二次规划问题的主要函数是quadprog。
求解无约束非线性规划问题的主要函数是fminbnd、fminunc和fminsearch。
求解约束非线性规划问题的主要函数是fgoalattain和fminimax。二、一般步骤线性规划问题三、线性规划数学模型四、线性规划例题3.确定约束条件：二次规划问题1.研究意义：
（1）最简单的非线性规划问题；
（2）求解方法比较成熟。
2.数学模型形式：

s.t.AX≤b（线性不等式约束条件）
AeqX=beq（线性等式约束条件）
lb≤X≤ub（边界约束条件）无约束非线性规划问题七、无约束非线性规划问题的函数1.使用格式：
[xopt,fopt]=fminbnd(fun,x1,x2,options)2.例题：
求解一维无约束优化问题f(x)=(x3+cosx+xlogx/ex)
在区间[0,1]中的极小值。
解：(1)编制求解优化问题的M文件。
%求解一维优化问题
fun=inline(‘(x^3+cos(x)+x*log(x))/exp(x)’,‘x’);%目标函数
x1=0;x2=1;%搜索区间
[xopt,fopt]=fminbnd(fun,x1,x2)
(2)编制一维函数图形的M文件。
ezplot(fun,[0,10])
title('(x^3+cosx+xlogx)/e^x')
gridon1.使用格式：
[xopt,fopt]=fminsearch(fun,x0,options)2.例题：求解二维无约束优化问题
f(x)=(x14+3x12+x22-2x1-2x2-2x12x2+6)的极小值。
解：(1)编制求解二维无约束优化问题的M文件。
%求解二维优化问题
fun='x(1)^4+3*x(1)^2+x(2)^2-2*x(1)-2*x(2)-2*x(1)^2*x(2)+6';
x0=[0,0];%初始点
[xopt,fopt]=fminsearch(fun,x0)
(2)讨论。
将目标函数写成函数文件的形式：
%目标函数文件search.m
functionf=search(x)
f=x(1)^4+3*x(1)^2+x(2)^2-2*x(1)-2*x(2)-2*x(1)^2*x(2)+6;
则命令文件变为：
%命令文件名称为eg9.m
x0=[0,0];%初始点
[xopt,fopt]=fminsearch(@search,x0)1.使用格式：
[x,fval,exitflag,output,grad,hessian]=fminunc(@fun,x0,options,P1,P2…)管道截面积：控制参数options控制参数options约束非线性规划问题1.数学模型形式：
minf（X）
s.t.AX≤b（线性不等式约束）
AeqX=beq（线性等式约束）
C(X)≤0（非线性不等式约束条件）
Ceq(X)=0（非线性等式约束）
Lb≤X≤Ub（边界约束条件）控制参数options控制参数options2829303132Theend!练习练习