逻辑函数的化简.ppt

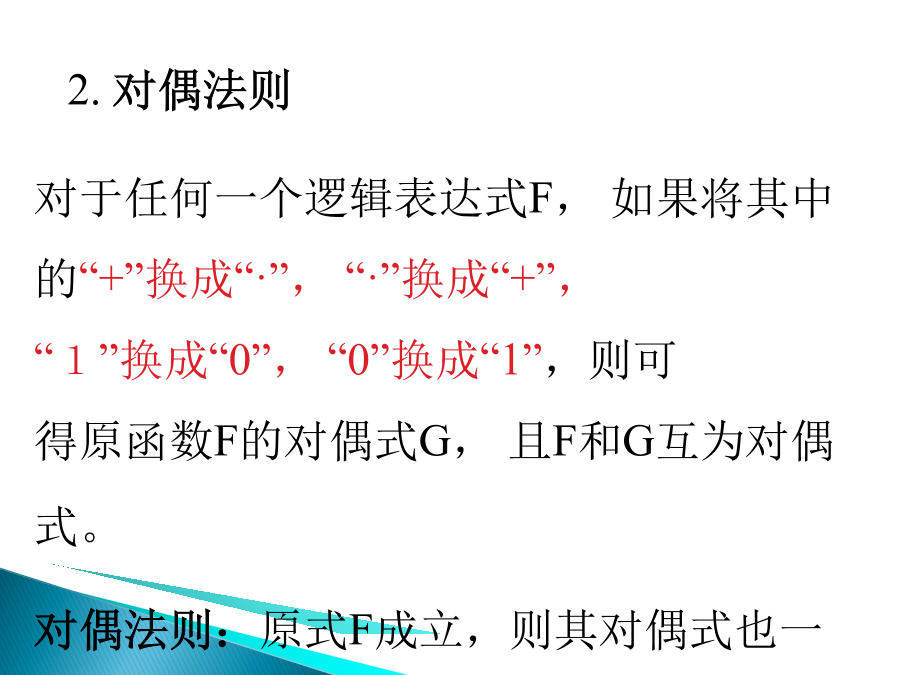
上节主要内容回顾本讲主要内容用真值表证明分配律：
A+BC=(A+B)(A+C)
两个变量的摩根定律的真值表证明：
吸收律证明：
A+AB=A(1+B)=A(因为1+B=1)多余项定律可推广为基本规则
1、代入规则：
逻辑等式中的任何变量A，都可用另一逻辑函数Z代替，等式仍然成立。例1证明2.对偶法则
对于任何一个逻辑表达式F，如果将其中的“+”换成“·”，“·”换成“+”，“１”换成“0”，“0”换成“1”，则可得原函数F的对偶式G，且F和G互为对偶式。
对偶法则：原式F成立，则其对偶式也一定成立。其对偶式为：3.反演法则例：利用反演法则求反：将原函数F中的“·”换成“+”,“+”换成“·”；“0”换成“1”，“1”换成“0”；原变量换成反变量，反变量换成原变量，长非号即两个或两个以上变量的非号不变，即可得反函数。如上例公式的应用：例：将函数与或表达式转换为其它形式。
解：（1）转换为与非-与非式。
将与或式两次取反，利用摩根定律可得代数法化简例：2、吸收法：应用以下定律例：例133、应用多余项定律例综合例子4、拆项法在函数中加入零项因子，利用加进的新项，进一步化简函数。
例
解【例13】：有原始逻辑函数表达式为

要求：
(1)画出原始逻辑表达式的逻辑图；
(2)用布尔代数简化逻辑表达式；
(3)画出简化逻辑表达式的逻辑图。化简：【例15】设计一个逻辑电路，当三个输入A,B,C中至少有两个为低时，该电路则输出为高。要求：(1)建立真值表；(2)从真值表写出布尔表达式；(3)如果可能，简化表达式；(4)画出逻辑电路图。
[解]
(1)由于有三个变量，真值表有8种输入组合。代数法化简存在的问题1.5卡诺图三个变量ABC有八个最小项：三变量最小项的编号2、逻辑函数的标准式——最小项标准式
全是由最小项组成的“与或”式叫做最小项标准式(不一定由全部最小项组成)。
由一般式获得最小项标准式4、卡诺图的结构—逻辑函数的图形表示1~5变量的卡诺图4、卡诺图上的有用组合相邻最小项合并规律
(1)两相邻项可合并为一项，消去一个取值不同的变量，保留相同变量；
(2)四相邻项可合并为一项，消去两个取值不同的变量，保留相同变量，标注为1→原变量，0→反变量；
(3)八相邻项可合并为一项，消去三个取值不同的变量，保留相同变量，标注与变量关系同上。
合并的规律是2n个最小项的相邻项可合并图1–8相邻最小项合并规律用卡诺图化简逻辑函数2、利用卡诺图化简逻辑函数
(1)将原始函数用卡诺图表示；
(2)根据最小项合并规律画圈，圈住全部“１”方格；
(3)每一个圈对应一个与项，然后再将各与项“或”起来得新函数。
3、画包围圈的规则是：
（1）要尽可能地使卡诺圈大，这样消去的变量就多，但每个圈中所包含的的方格数只能是2n，且只有相邻的1才能被圈在一起；
（2）使卡诺圈数目最少,这样逻辑函数的与项就少，但所有填1的方格必须被圈，不能遗漏；
（3）每个为1的方格可被圈多次，但每个圈中至少有一个1只被圈过一次；

化简举例：例：将用卡诺图表示。
解我们逐项用卡诺图表示，例如
在B=1,C=0对应的方格(不管A，D取值)，得m4、m5、m12、m13，在对应位置填1；例：化简第二步：画卡诺圈圈住全部“１”方格。
第三步：组成新函数。第四步：画出逻辑电路。例：化简图1–15化简过程及逻辑图图1–16化简过程及逻辑图无关项及无关项的应用图1–25考虑无关项函数化简例：化简例：化简1.6数字集成电路集成逻辑门电路的外特性
扇出系数Nc
门电路通常只有一个输出端，但它能与下一级的多个门的输入端连接。一个门的输出端所能连接的下一级门输入端的个数称为该门电路的扇出系数。或称负载能力。TTL一般门电路的扇出系数为8，驱动门的扇出系数可达25。CMOS门的扇出系数更大一些。
平均传输延迟时间
是反映门电路工作速度的一个重要参数。以非门为例，在输入端加上一个正方波,则需要一定的时间间隔才能从输出端得到一个负方波。这两个方波的时间关系如图所示。若定义输入波形前沿的50%到输出波形前沿的50%之间的时间间隔t1为前沿延迟；同样，若定义t2为后沿延迟，则它们的平均值称为平均传输延迟时间简称平均时延。

开门电平U0H与关门电平U0L
表示逻辑值1的最小高电平UOH称为开门电平
表示逻辑值0的最大低电平UOL称为关门电平课堂练习精品课件！精品课件！作业