
连续时间信号的抽样与量化信号与系统.ppt

YY****。。








亲,该文档总共78页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

连续时间信号的抽样与量化信号与系统.ppt
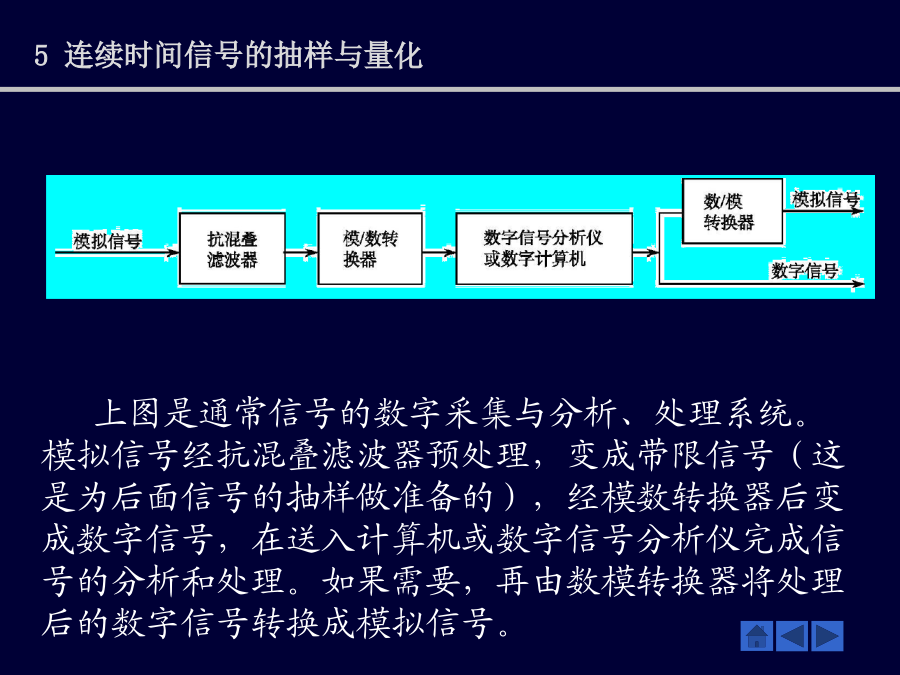
第5章连续时间信号的抽样与量化§5.1引言连续时间信号在进入数字系统之前,有一个如何将模拟信号转化为数字信号的问题,即信号的数字采集,这种转化应是以不丢失模拟信号的信息为原则,本章基于这样的原则,讨论模拟信号数字采集的有关问题。研究如何从连续时间信号的离散时间样本不失真地恢复原来的连续时间信号。讨论与时域抽样完全对偶的频域抽样。研究如何对一个连续时间信号进行均匀量化问题。上图是通常信号的数字采集与分析、处理系统。模拟信号经抗混叠滤波器预处理,变成带限信号(这是为后面信号的抽样做准备的),经模数转换器后变成

连续时间信号的抽样与量化信号与系统.ppt
第5章连续时间信号的抽样与量化§5.1引言连续时间信号在进入数字系统之前,有一个如何将模拟信号转化为数字信号的问题,即信号的数字采集,这种转化应是以不丢失模拟信号的信息为原则,本章基于这样的原则,讨论模拟信号数字采集的有关问题。研究如何从连续时间信号的离散时间样本不失真地恢复原来的连续时间信号。讨论与时域抽样完全对偶的频域抽样。研究如何对一个连续时间信号进行均匀量化问题。上图是通常信号的数字采集与分析、处理系统。模拟信号经抗混叠滤波器预处理,变成带限信号(这是为后面信号的抽样做准备的),经模数转换器后变成

连续时间信号与系统.ppt
Chapter0连续时间信号与系统§1.1概论§1.1概论§1.2连续时间信号最常用的信号最常用的信号最常用的信号最常用的信号最常用的信号最常用的信号最常用的信号最常用的信号单位冲激函数δ(t)δ(t)函数的特性δ(t)函数的特性δ(t)函数的特性δ(t)函数的特性§1.3用δ(t)函数来表示信号§1.4线性时不变系统§1.4线性时不变系统§1.5系统的单位冲激响应§1.5信号通过线性时不变系统连续时间信号与系统的频域分析时域分析与频域分析§1.6周期函数的傅立叶级数§1.6周期函数的傅立叶级数§1.6周

连续信号的抽样.pptx
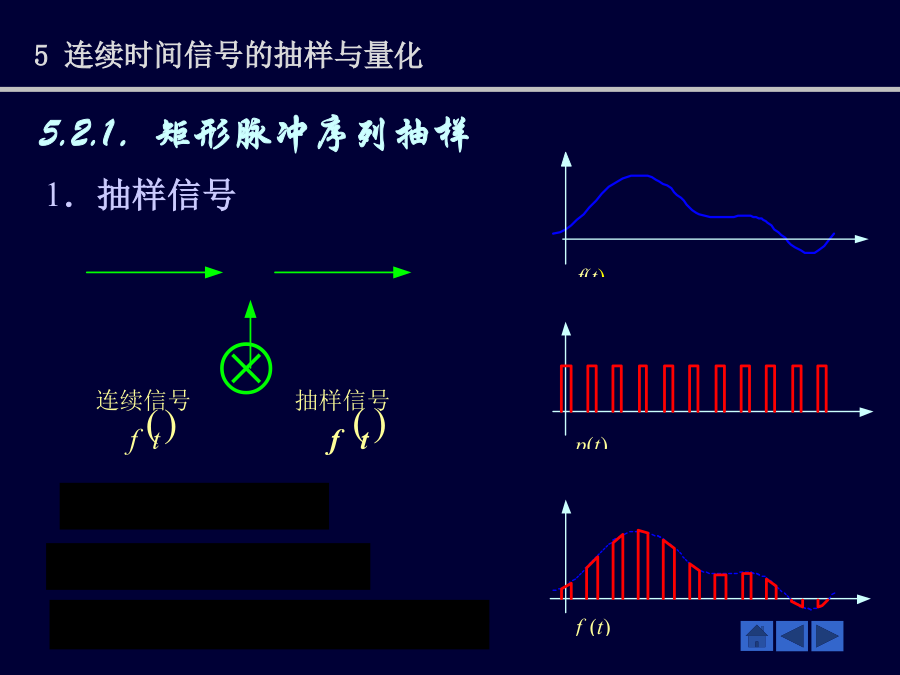
复习第一章第四节连续时间信号旳抽样(P33页)一、引言1、抽样2、抽样器3、研究内容4、抽样方式二、理想抽样理想抽样输出为:理想抽样后信号频谱:奈奎斯特抽样定理折叠频率为防止混叠采用措施抽样旳恢复将抽样后旳信号经过理想低通滤波器:就可得到原信号旳频谱:理想低通滤波器旳冲激响应为:理想低通滤波器旳输出:抽样内插公式内插函数内插函数从上图看出:(1)在抽样点mT上,函数值为1,其他抽样点上,函数值为零。(2)xa(t)等于各xa(mT)乘上相应旳内插函数旳总和。(3)在每一抽样点上,只有该点所相应旳内插函数不

抽样信号的量化-副本.ppt
通信原理通信原理第9章模拟信号的数字传输第9章模拟信号的数字传输第9章模拟信号的数字传输第9章模拟信号的数字传输第9章模拟信号的数字传输第9章模拟信号的数字传输第9章模拟信号的数字传输第9章模拟信号的数字传输第9章模拟信号的数字传输第9章模拟信号的数字传输第9章模拟信号的数字传输第9章模拟信号的数字传输第9章模拟信号的数字传输第9章模拟信号的数字传输第9章模拟信号的数字传输第9章模拟信号的数字传输第9章模拟信号的数字传输第9章模拟信号的数字传输第9章模拟信号的数字传输第9章模拟信号的数字传输第9章模拟信
