蒙特卡洛方法的应用.ppt

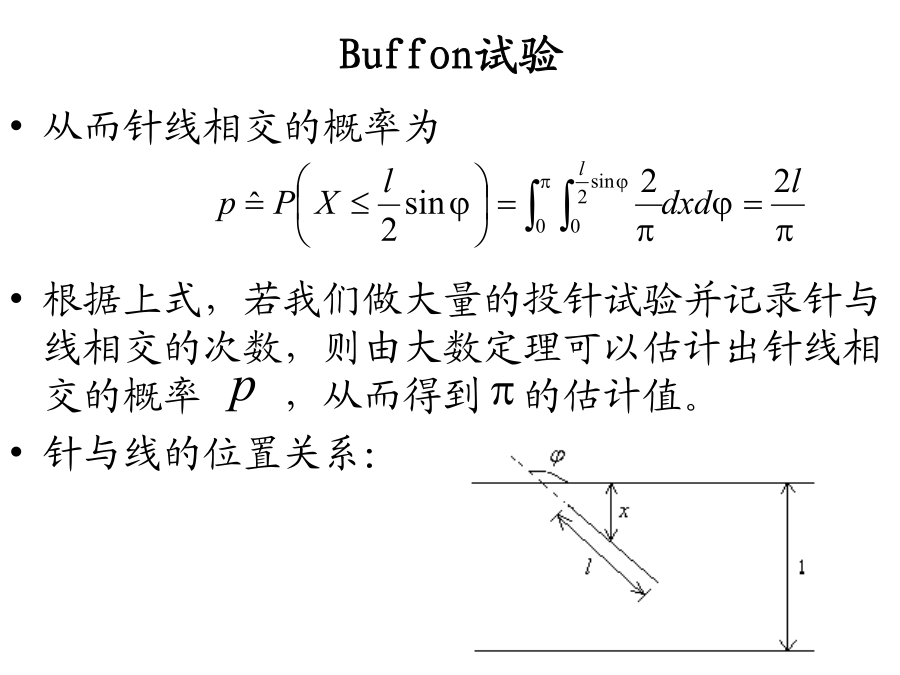
实验目的一、MC的起源和发展事实上，MonteCarlo方法的基本思想很早以前就被人们所发现和利用。早在17世纪，人们就知道用事件发生的“频率”来决定事件的“概率”。18世纪下半叶的法国学者Buffon提出用投针试验的方法来确定圆周率π的值。这个著名的Buffon试验是MonteCarlo方法的最早的尝试！历史上曾有几位学者相继做过这样的试验。不过呢，他们的试验是费时费力的，同时精度不够高，实施起来也很困难。然而，随着计算机技术的飞速发展，人们不需要具体实施这些试验，而只要在计算机上进行大量的、快速的模拟试验就可以了。Buffon试验Buffon试验functionpiguji=buffon(llength,mm)
%llength是针的长度
%mm是随机实验次数
frq=0;
xrandnum=unifrnd(0,0.5,1,mm);
phi=unifrnd(0,pi,1,mm);
forii=1:mm
if(xrandnum(1,ii)<=(llength*sin(phi(1,ii))/2))
frq=frq+1;
end
end
piguji=2*llength/(frq/mm)>>buffon(.6,1000)piguji=3.1662
>>buffon(.6,10000)piguji=3.1072
>>buffon(.6,100000)piguji=3.1522
>>buffon(.6,1000000)piguji=3.1386
>>buffon(.6,1000000)piguji=3.1451
>>buffon(.6,1000000)piguji=3.1418
>>buffon(.6,1000000)piguji=3.1448
>>buffon(.6,1000000)piguji=3.1405
>>buffon(.6,1000000)piguji=3.1394二、MC的原理思路3、根据概率模型的特点和随机变量的分布特性，设计和选取合适的抽样方法，并对每个随机变量进行抽样（包括直接抽样、分层抽样、相关抽样、重要抽样等）。
4、按照所建立的模型进行仿真试验、计算，求出问题的随机解。
5、统计分析模拟试验结果，给出问题的估计以及其精度估计。
6、必要时，还应改进模型以降低估计方差和减少试验费用，提高模拟计算的效率。收敛性:由大数定律,Monte-Carlo模拟的收敛是以概率而言的．
误差:用频率估计概率时误差的估计，可由中心极限定理，给定置信水平的条件下，有：

模拟次数:由误差公式得

三、MC的应用举例1、定积分的MC计算在计算积分上，MC的实用场合是计算重积分

其中是维空间的点，当较大时，用MC方法比一般的数值方法有优点，主要是它的误差与维数无关。随机投点法那么我们可以得到的一个估计

具体试验步骤为

求解定积分的算例functionresult=sjtdf(a,b,m,mm)
%a是积分的下限
%b是积分的上限
%m是函数的上界
%mm是随机实验次数
frq=0;
xrandnum=unifrnd(a,b,1,mm);
yrandnum=unifrnd(0,m,1,mm);
forii=1:mm
if(cos(xrandnum(1,ii))+2>=yrandnum(1,ii))
frq=frq+1;
end
end
result=frq*m*(b-a)/mm注1随机投点法的思想简单明了，且每次投点结果服从二项分布，故，其中

注2可证是的无偏估计。若用估计的标准差来衡量其精度，则估计的精度的阶为。
注3这里，定积分的解，就对应我们选定的随机变量的概率值。例的计算>>sjtdf_pi1(1000)piguji=3.0520
>>sjtdf_pi1(10000)piguji=3.1204
>>sjtdf_pi1(100000)piguji=3.1296sjtdf_pi2(100)piguji=3.2000
>>sjtdf_pi2(1000)piguji=3.2120
>>sjtdf_pi2(10000)piguji=3.1260
>>sjtdf_pi2(100000)piguji=3.1373样本平均值法设是来自的随机数，则的一个估计为

具体步骤为

注可证是的无偏估计。一般而言，样本均值法要比随机投点法更有效。求解定积分的算例functionresult=ybjzf(a,b,m,mm)
%a是积分的下限
%b是积分的上限
%积分函数cos(x)+2
%mm是随机实验次数
sum=0;
xrandnum=unifrnd(a,b,1,mm);
forii=1:mm
sum=sum+cos(xrandnum(1,ii))+2;
end
result=sum*(b-a)/mm例的计算几种降低估