稳定性与李雅普诺夫方法.ppt

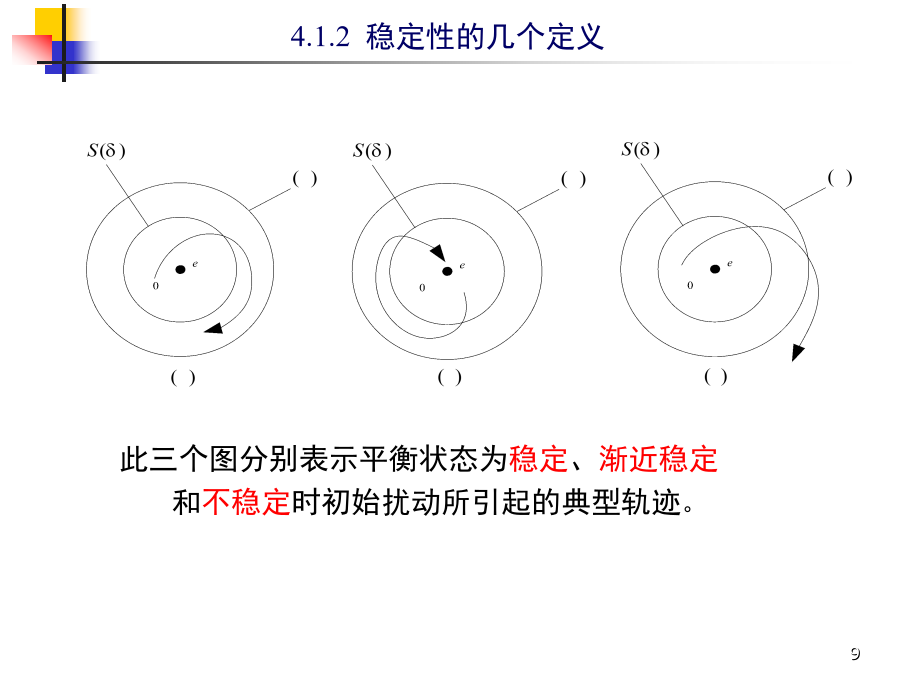
第4章稳定性与李雅普诺夫方法4.1李雅普诺夫关于稳定性的定义平衡状态不一定存在，也不一定唯一。
如：其平衡状态有：

稳定性是相对于平衡点而言的！4.1.2稳定性的几个定义
1.Lyapunov意义下的稳定2.渐近稳定若，则称为大范围(全局)渐近稳定。对于某个实数和任意，在超球域

内始终存在状态，使得从该状态开始的运动轨迹要
突破超球域。此三个图分别表示平衡状态为稳定、渐近稳定
和不稳定时初始扰动所引起的典型轨迹。4.2李雅普诺夫第一法线性定常系统，

在平衡状态渐近稳定的充要条件是矩阵A的所有特征值均具有负实部。此为状态稳定性，或称内部稳定性。输出稳定性：如果系统对于有界输入u所引起的输出y是有界的，则称系统为输出稳定。BIBO稳定（BoundedInputBoundedOutput）【例4-1】设，为平衡点。
将在邻域内展成泰勒级数，得
其中4.2.2非线性系统的稳定性4.2.2非线性系统的稳定性（3），则称是负定的。例例设2.二次型标量函数二次型函数，若P为实对称阵，则必存在正交矩阵T，
通过变换，使之化为：矩阵P的符号性质定义如下：
设P为n×n实对称阵，为由P决定的二次型函数，则
（1）正定，则P正定矩阵，记为P>0;
（2）负定，则P负定矩阵，记为P<0;
（3）半正定，则P半正定矩阵，记为P≥0;
（4）半负定，则P半负定矩阵，记为P≤0;3、希尔维斯特判据
设实对称阵

为其各阶顺序主子式，即

矩阵P或V(x)定号性的充要条件是：(2)若，则P负定；解：二次型可以写为4.3李雅普诺夫第二法4.3.2几个稳定性判据4.3.2几个稳定性判据4.3.2几个稳定性判据说明：
（1），则此时，系统轨迹将在某个曲面上，而不能收敛于原点，因此不是渐近稳定。
（2）不恒等于0，说明轨迹在某个时刻与曲面相交，但仍会收敛于原点，所以是渐近稳定。

（3）稳定判据只是充分条件而非必要条件！解:显然，原点是系统平衡点，
取，则

又因为当时，有，所以系统在原点处
是大范围渐近稳定的。【例4-5】已知系统的状态方程，试分析平衡状态的稳定性。

解：线性系统，故是其唯一平衡点。
将矩阵形式的状态方程展开得到：

取标量函数(李雅谱诺夫函数)：

另选一个李雅普诺夫函数：解:系统具有唯一的平衡点。取

则

于是知系统在原点处不稳定。
4.3.3对李雅谱诺夫函数的讨论
（1）V(x)是正定的标量函数，V(x)具有一阶连续偏导数；
（2）并不是对所有的系统都能找到V(x)来证明该系统稳定或者不稳定；
（3）V(x)如果能找到，一般是不唯一的，但关于稳定性的结论是一致的；
（4）V(x)最简单的形式是二次型；
（5）V(x)只是提供平衡点附近的运动情况，丝毫不能反映域外运动的任何信息；
（6）构造V(x)需要一定的技巧。4.4李雅普诺夫方法在线性系统中的应用设线性定常系统为：

则平衡状态为大范围渐近稳定的充要条件是：对任意给定的正定实对称矩阵Q，必存在正定的实对称矩阵P，满足李雅普诺夫方程：

且就是李雅普诺夫函数。
证明：略。说明：
（1）一般先取正定矩阵Q，带入李雅谱诺夫方程，求出P，判别P的正定性，从而判断系统的稳定性；
（2）以方便计算，通常取Q＝I。
（3）若沿任一轨线不恒等于零，那么Q可取半正定，

即可取计算更简单。

（4）判据是充分必要条件例4-9:分析下列系统稳定性

解：令，

则由得解上述矩阵方程，即得【例4-10】系统状态方程

确定使系统稳定的K的取值范围。
解：因detA≠0，故原点为系统唯一平衡点。取Q为：则由得本章小结