
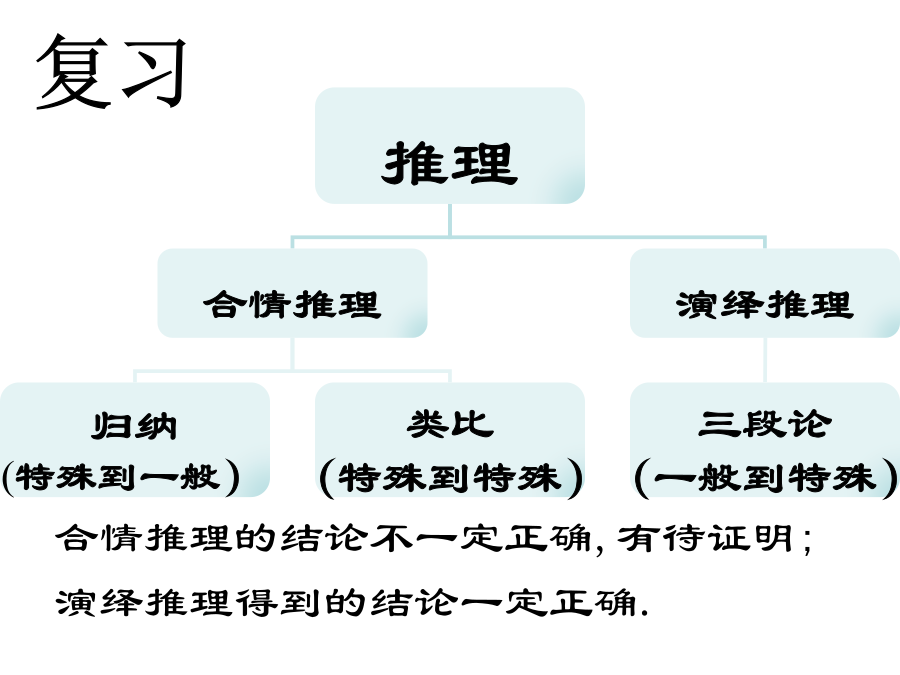
2.2-直接证明与间接证明(三种方法)(人教A选修1-2).ppt

赫赫****等你






亲,该文档总共24页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

2.2-直接证明与间接证明(三种方法)(人教A选修1-2).ppt
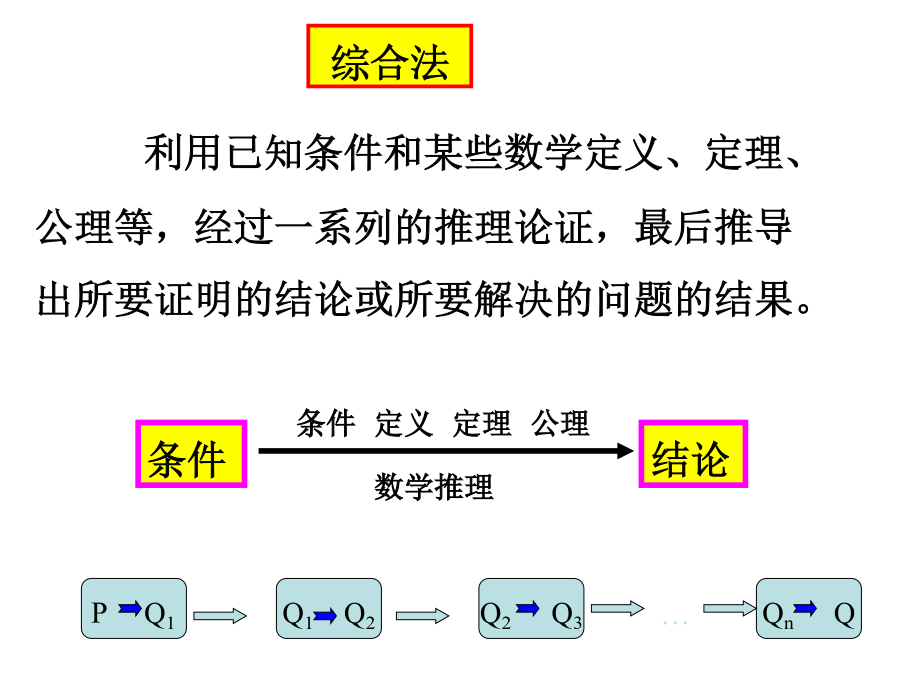
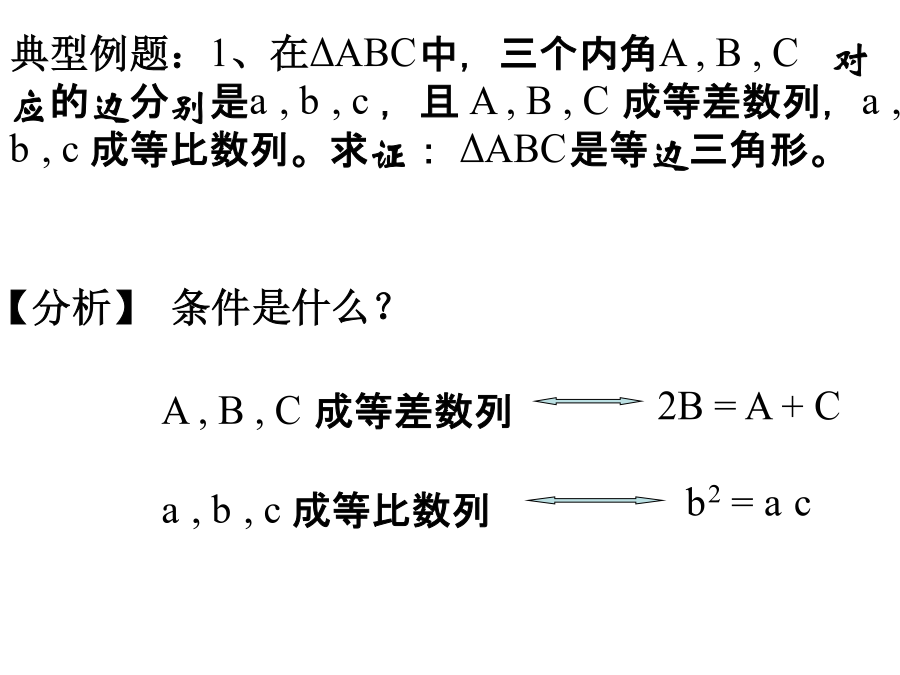
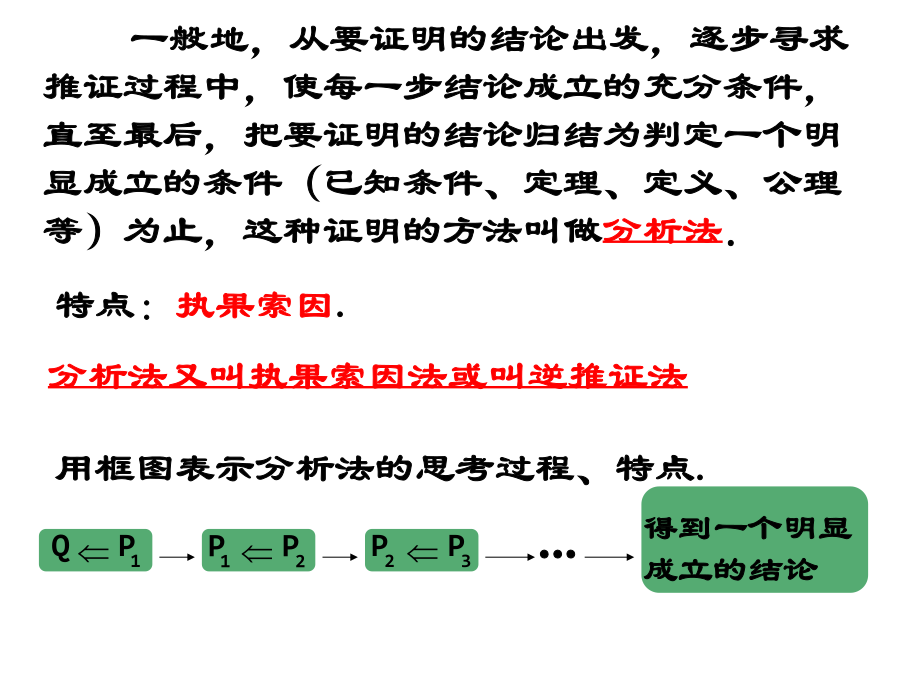
2.2直接证明与间接证明复习已知a>0,b>0,求证a(b2+c2)+b(c2+a2)≥4abc综合法变式1:变式3:典型例题:1、在ΔABC中,三个内角A,B,C对应的边分别是a,b,c,且A,B,C成等差数列,a,b,c成等比数列。求证:ΔABC是等边三角形。典型例题:1、在△ABC中,三个内角A、B、C对应的边分别为a、b、c,且A、B、C成等差数列,a、b、c成等比数列,求证△ABC为等边三角形.回顾基本不等式:(a>0,b>0)的证明.一般地,从要证明的结论出发,逐步寻求推证过程中,使每一步结论

数学:2.2《直接证明与间接证明》测试2(新人教A版选修1—2)-(2).doc
高中新课标选修(1-2)直接证明与间接证明测试题一、选择题1.下列说法不正确的是()A.综合法是由因导果的顺推证法B.分析法是执果索因的逆推证法C.综合法与分析法都是直接证法D.综合法与分析法在同一题的证明中不可能同时采用答案:D2.用反证法证明一个命题时,下列说法正确的是()A.将结论与条件同时否定,推出矛盾B.肯定条件,否定结论,推出矛盾C.将被否定的结论当条件,经过推理得出的结论只与原题条件矛盾,才是反证法的正确运用D.将被否定的结论当条件,原题的条件不能当条件答案:B3.若是不全相等的实数,求证:

数学:2.2《直接证明与间接证明》测试1(新人教A版选修1—2)-(3).doc
高中新课标选修(1-2)直接证明与间接证明测试题一、选择题1.证明不等式的最适合的方法是()A.综合法B.分析法C.间接证法D.合情推理法答案:B2.对一个命题的证明,下列说法错误的是()A.若能用分析法,必能用综合法B.若用综合法或分析法证明难度较大时,可考虑分析法与综合法的合用等方法C.若用直接证法难度较大时,可考虑反证法D.用反证法就是要证结论的反面成立答案:D3.设都是正数,则三个数()A.都大于2B.至少有一个大于2C.至少有一个不大于2D.至少有一个不大于2答案:C4.设,,,,则有()A.B

(完整版)2.2-直接证明与间接证明(三种方法)(人教A选修1-2)(共24张PPT).ppt
2.2直接证明与间接证明复习已知a>0,b>0,求证a(b2+c2)+b(c2+a2)≥4abc综合法变式1:变式3:典型例题:1、在ΔABC中,三个内角A,B,C对应的边分别是a,b,c,且A,B,C成等差数列,a,b,c成等比数列。求证:ΔABC是等边三角形。典型例题:1、在△ABC中,三个内角A、B、C对应的边分别为a、b、c,且A、B、C成等差数列,a、b、c成等比数列,求证△ABC为等边三角形.回顾基本不等式:(a>0,b>0)的证明.一般地,从要证明的结论出发,逐步寻求推证过程中,使每一步结论

【精选】直接证明与间接证明》课件新人教选修.ppt
新课标人教版课件系列2.2《直接证明与间接证明》教学目标直接证明直接证明(问题情境)直接证明直接证明(学生活动)直接证明直接证明(数学理论)直接证明直接证明(例题)直接证明直接证明直接证明(练习)直接证明(练习)直接证明直接证明(回顾小结)2.类比下列平面图形的性质写出空间图形的性质:类比的风险类比推理类比推理归纳推理和类比推理的过程1、水果:苹果A.香梨:黄梨B.树木:树枝C.经济适用房:奔驰D.山:高山作业:35页习题2-1.1题公鸡蛋从前有一个国王想吃公鸡蛋限丞相三天之内找来.否则
