现代信号处理自适应信号处理.ppt

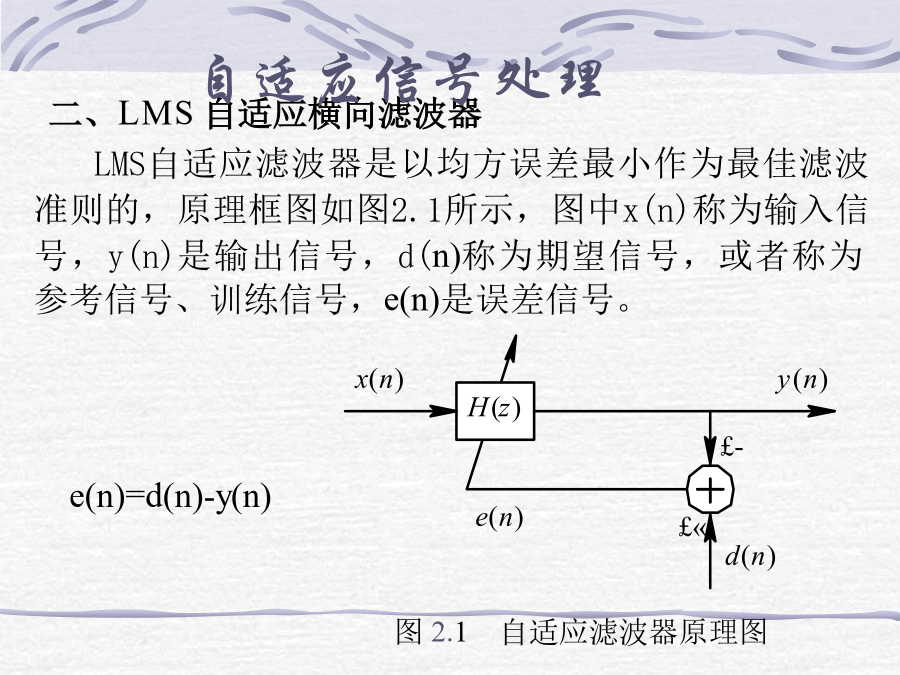
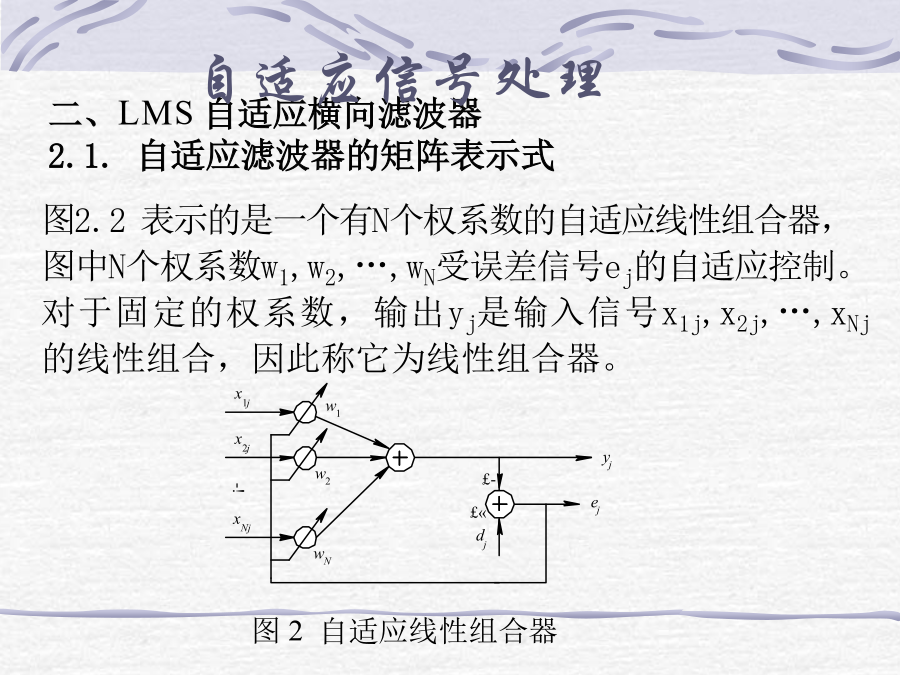
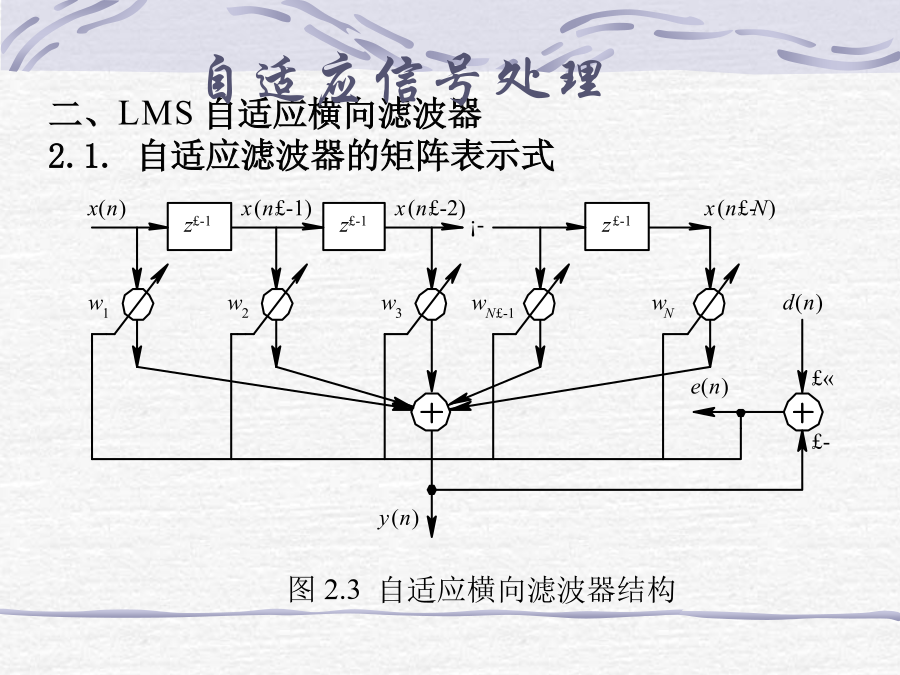
自适应信号处理自适应滤波器和维纳滤波器一样，都是符合某种准则的最佳滤波器。维纳滤波器的参数是固定的，适用于平稳随机信号的最佳滤波，但要设计这种滤波器，必须要求输入信号是平稳的，且必须信号和噪声自相关特性。在实际中，常常无法知道这些特性，且信号和噪声自相关函数还会随时间变化，因此实现最佳滤波是困难的。自适应滤波器的特点是：滤波器的参数可以按照某种准则自动地调整到满足最佳滤波的要求；实现时不需要任何关于信号和噪声的自相关特性，尤其当输入统计特性变化时，自适应滤波器都能调整自身的参数来满足最佳滤波的需要，即具有学习和跟踪的性能。自适应滤波器发展很快，已广泛地用于系统模型识别，通信信道的自适应均衡，雷达与声纳的波束形成，减少或消除心电图中的周期干扰，噪声中信号的检测、跟踪、增强和线性预测等。LMS自适应滤波器是以均方误差最小作为最佳滤波准则的，原理框图如图2.1所示，图中x(n)称为输入信号，y(n)是输出信号，d(n)称为期望信号，或者称为参考信号、训练信号，e(n)是误差信号。

图2.1自适应滤波器原理图其中自适应滤波器H(z)的系数根据误差信号，通过一定的自适应算法，不断地进行改变,使输出y(n)最接近期望信号d(n),这里暂时假定d(n)是可以利用的，实际中，d(n)要根据具体情况进行选取,能够选到一个合适的信号作为期望信号，是设计自适应滤波器的一项重要的工作。如果真正的d(n)可以获得，我们将不需要做任何自适应滤波器。图2.2表示的是一个有N个权系数的自适应线性组合器，图中N个权系数w1,w2,…,wN受误差信号ej的自适应控制。对于固定的权系数，输出yj是输入信号x1j,x2j,…,xNj的线性组合，因此称它为线性组合器。

图2自适应线性组合器这里的x1j,x2j,…,xNj可以理解为是从N个不同的信号源到达的瞬时输入，是一个多输入系统，也可以是同一个信号源的N个序贯样本，如图3所示，因此它是一个单输入系统，实际上也是一个自适应横向滤波器。其输出y(n)用滤波器的单位脉冲响应表示成下式：图2.3自适应横向滤波器结构二、LMS自适应横向滤波器二、LMS自适应横向滤波器误差信号被用来作为权系数的控制信号。下面采用均方误差最小的准则，求最佳权系数。由(2.1.4)式，均方误差为：令：将(2.1.6)、(2.1.7)式代入(2.1.5)式，得到(2.1.8)式表明，当输入信号和期望信号是平稳随机信号时,均方误差信号是权系数的二次函数，即将该式展开时，公式中的权系数均以它的一次幂或二次幂出现。如果只有一个权系数,则是的口向上的抛物线；如果有两个权系数,则是它们的口向上的抛物面；对于两个权系数以上的情况，则属于超抛物面性质，它具有唯一的极小点。在自适应信号处理中是一个重要的函数，经常称它为性能函数。为选择权系数，使性能函数到达它的最小点，一些有用的自适应方法都是基于梯度法的，用表示的梯度向量，它是用对每个权系数求微分而形成的一个列向量，用公式表示如下：可以用(2.1.8)式对W求导得到：
(2.2.2)
令上式等于0,得到最佳权矢量表达式：
(2.2.3)
对比前面维纳滤波器的最佳解，结果是一样的。上式也称为维纳权矢量。在维纳滤波器中，当滤波器的单位脉冲响应取最佳值时，其误差信号和输入信号是正交的；这里也有相同的结果，当权矢量取最佳值时，梯度为0。当自适应滤波器的权系数满足上式时，均方误差将取最小值。将(3.2.11)式代入(3.2.8)式得到最小均方误差：或者将上式取转置，用下式表示：

通过式子(2.1.12)可以准确的求出，但在权的数目N很大或输入数据率很高的时候，用这种方法直接求解会遇到很大困难，它不仅需要计算N×N矩阵的逆，还需要测量或估算N(N+1)/2个自相关或互相关函数才能得到和的各矩阵元素。不仅如此，当输入统计特性发生某种变化时，还必须重新作相应的计算，这样就存在收敛速度慢的问题。所以，推出了更有实用价值的递推估计等算法。从非负二次均方误差函数的几何性质来看，权向量从某一初始值出发，通过不断调整自身数值使均方误差ξ达到最小。最陡下降法就是下一个权矢量为现在权矢量加上一个正比于梯度的负值变化量，即是一个控制稳定性和收敛速度的参量，是调整步长的一个常数，也称为步长因子。
某一点的梯度方向即为该点变化率最大的方向，也是下降最快的方向，因此这种方法被称为最陡下降法。按(3.2.14)式，当时，将以的方向，即最陡下降的方向向W*靠拢，靠拢步距由确定。当达到的最小点时，即：由最陡下降法的递推公式不难分析出它的收敛条件，即当迭代次数j趋于∞时，权系数收敛最佳时的条件。得出只有当：
(2.3.2)

(2.3.3)
满足时，才能得到：。(2.3.3)式即是最陡下降法的收敛条件，式中是的最大特征值。为保证收敛，μ