
信号与系统期末考试试题(有答案的)(精品文档)-共10页.pdf

波峻****99








在线预览结束,喜欢就下载吧,查找使用更方便
相关资料

信号与系统期末考试试题(有答案的)(精品文档)-共10页.pdf
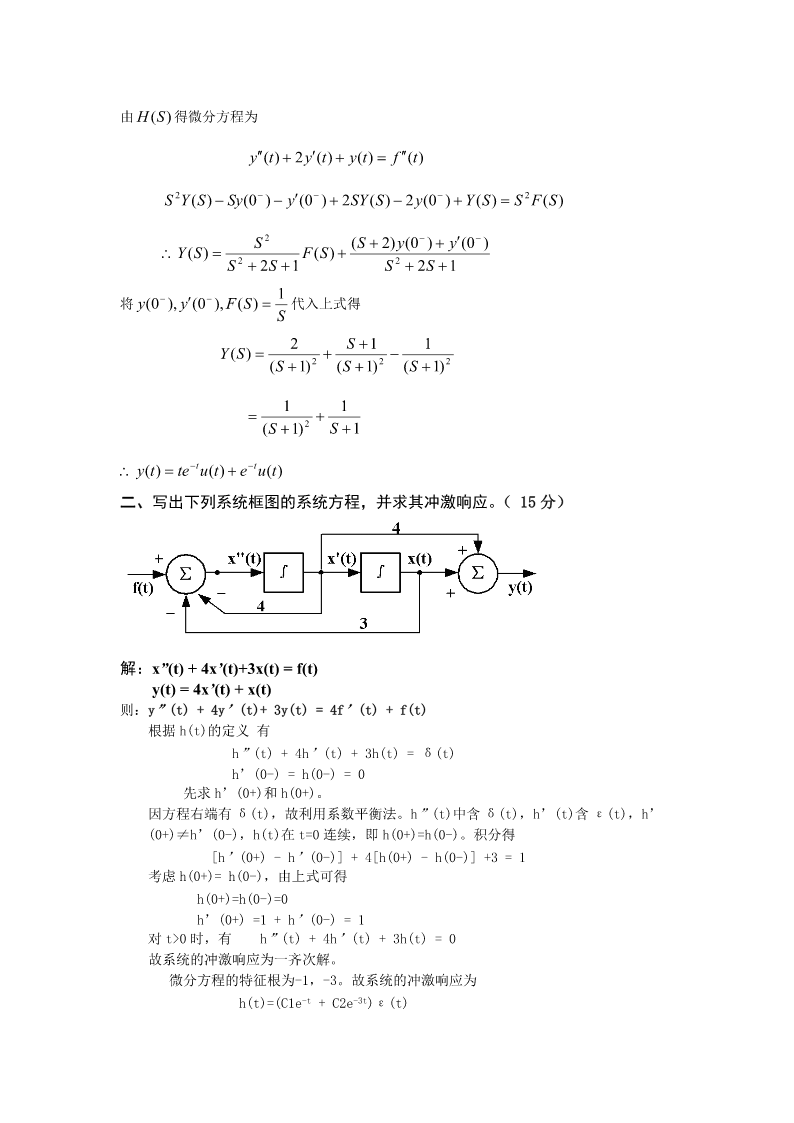
信号与系统期末考试试题一、选择题(共10题,每题3分,共30分,每题给出四个答案,其中只有一个正确的)1、卷积f1(k+5)*f2(k-3)等于。(A)f1(k)*f2(k)(B)f1(k)*f2(k-8)(C)f1(k)*f2(k+8)(D)f1(k+3)*f2(k-3)2、积分(t2)(12t)dt等于。(A)1.25(B)2.5(C)3(D)53、序列f(k)=-u(-k)的z变换等于。zz11(A)(B)-(C)(D)z1z1z1z14、若y(t)=f(t)*h(t),则f

信号与系统期末考试试题(有答案的)(精品文档)-共10页.pdf
信号与系统期末考试试题一、选择题(共10题,每题3分,共30分,每题给出四个答案,其中只有一个正确的)1、卷积f1(k+5)*f2(k-3)等于。(A)f1(k)*f2(k)(B)f1(k)*f2(k-8)(C)f1(k)*f2(k+8)(D)f1(k+3)*f2(k-3)2、积分(t2)(12t)dt等于。(A)1.25(B)2.5(C)3(D)53、序列f(k)=-u(-k)的z变换等于。zz11(A)(B)-(C)(D)z1z1z1z14、若y(t)=f(t)*h(t),则f

信号与系统期末考试试卷(有详细答案)(精品文档)-共9页.pdf
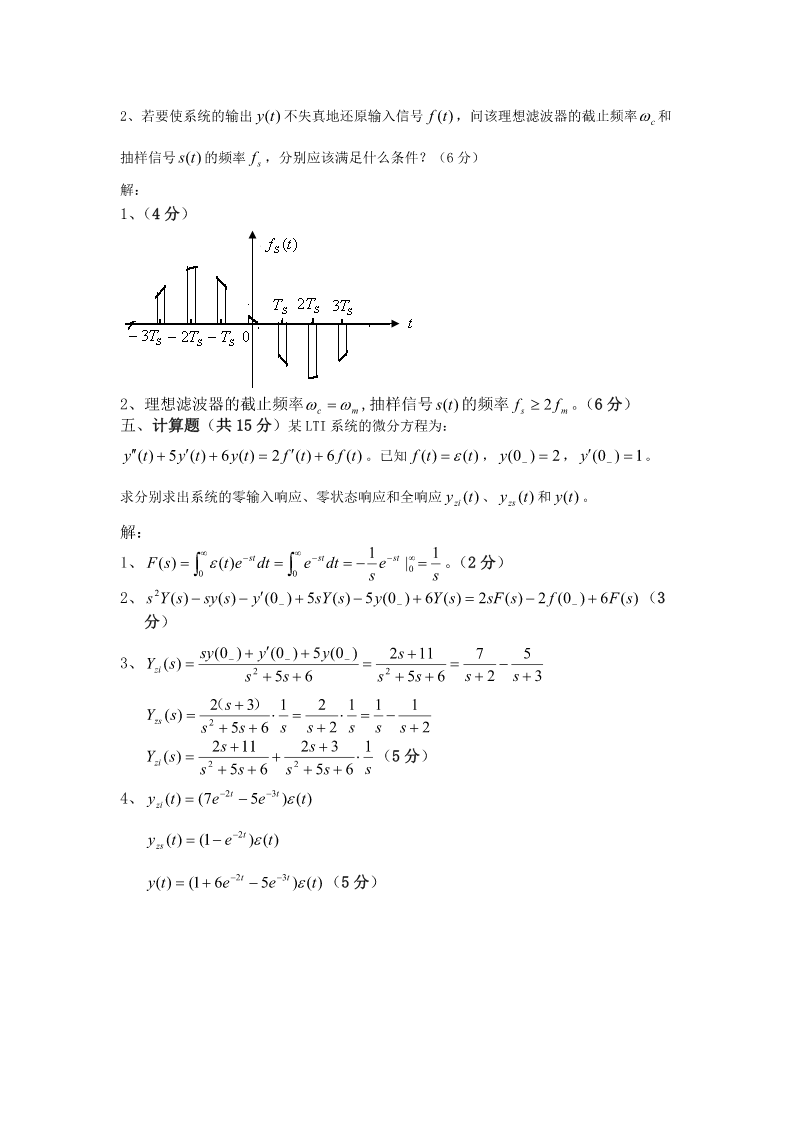
《信号与系统》考试试卷(时间120分钟)院/系专业姓名学号题号一二三四五六七总分得分一、填空题(每小题2分,共20分)得分de(t)1.系统的激励是e(t),响应为r(t),若满足r(t),则该系统为线性、时不变、因dt果。(是否线性、时不变、因果?)2.求积分(t21)(t2)dt的值为5。3.当信号是脉冲信号f(t)时,其低频分量主要影响脉冲的顶部,其高频分量主要影响脉冲的跳变沿。4.若信号f(t)的最高频率是2kHz,则f(2t)的乃奎斯特抽样频率为8kHz。5.信号在通过线性系统不
信号与系统实验(精品文档)-共4页.pdf
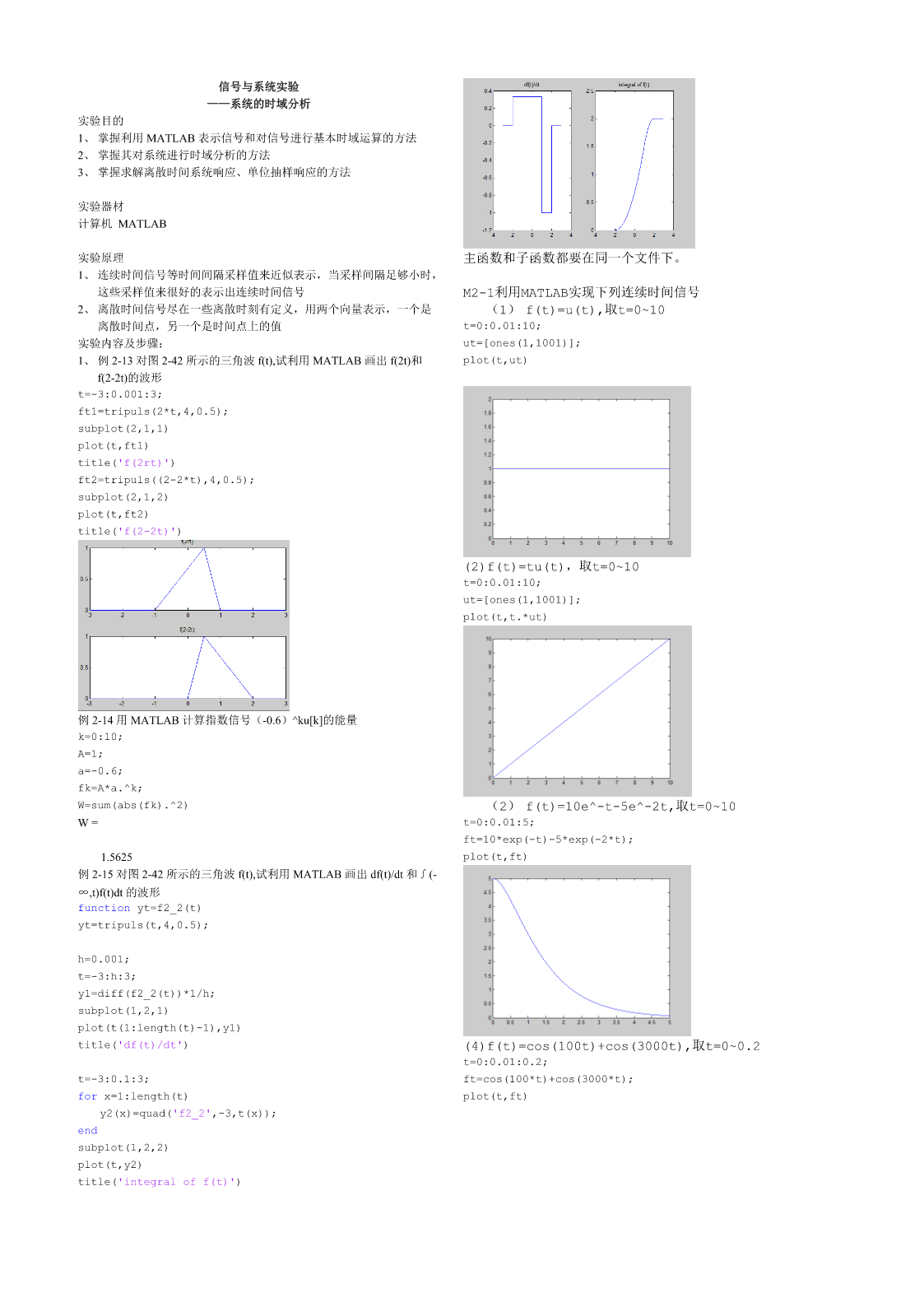
信号与系统实验——系统的时域分析实验目的1、掌握利用MATLAB表示信号和对信号进行基本时域运算的方法2、掌握其对系统进行时域分析的方法3、掌握求解离散时间系统响应、单位抽样响应的方法实验器材计算机MATLAB实验原理主函数和子函数都要在同一个文件下。1、连续时间信号等时间间隔采样值来近似表示,当采样间隔足够小时,这些采样值来很好的表示出连续时间信号M2-1利用MATLAB实现下列连续时间信号2、离散时间信号尽在一些离散时刻有定义,用两个向量表示,一个是(1)f(t)=u(t),取t=0~10离散时间点,
信号与系统实验(精品文档)-共4页.pdf
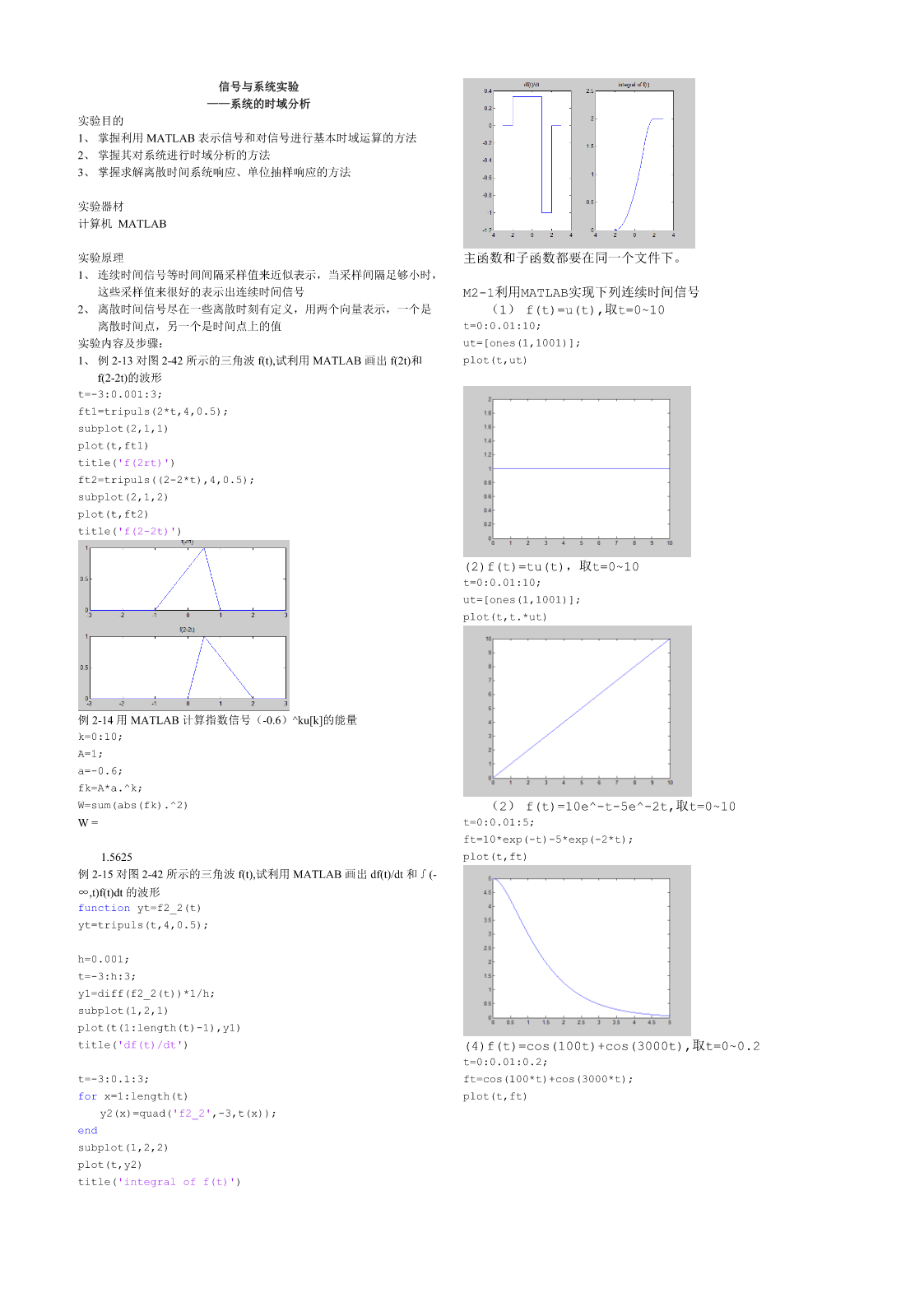
信号与系统实验——系统的时域分析实验目的1、掌握利用MATLAB表示信号和对信号进行基本时域运算的方法2、掌握其对系统进行时域分析的方法3、掌握求解离散时间系统响应、单位抽样响应的方法实验器材计算机MATLAB实验原理主函数和子函数都要在同一个文件下。1、连续时间信号等时间间隔采样值来近似表示,当采样间隔足够小时,这些采样值来很好的表示出连续时间信号M2-1利用MATLAB实现下列连续时间信号2、离散时间信号尽在一些离散时刻有定义,用两个向量表示,一个是(1)f(t)=u(t),取t=0~10离散时间点,
