
数值计算中的误差.ppt

YY****。。









亲,该文档总共60页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料
数值计算中的误差.ppt
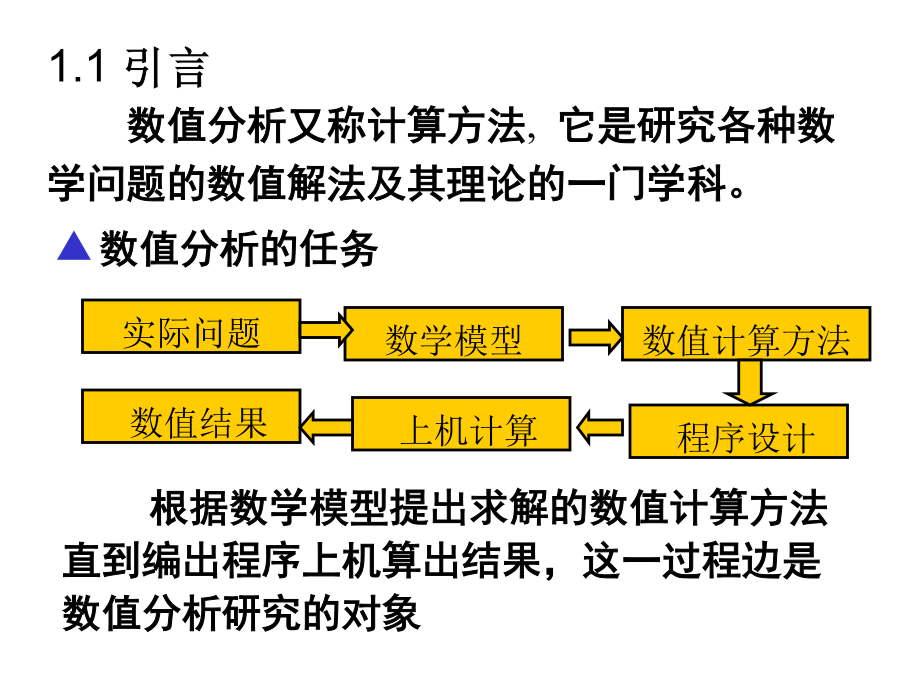
Tel:86613747E-mail:lss@zjtcm.net授课:68学分:4在数学发展中,理论和计算是紧密联系的。现代计算机的出现为大规模的数值计算创造了条件,集中而系统的研究适用于计算机的数值方法变得十分迫切和必要。数值计算方法正是在大量的数值计算实践和理论分析工作的基础上发展起来的,它不仅仅是一些数值方法的简单积累,而且揭示了包含在多种多样的数值方法之间的相同的结构和统一的原理。数值算法是进行科学计算必不可缺少的起码常识;更为重要的是通过对它们的讨论,能够使人们掌握设计数值算法的基本方法和一般原

计算声学数值计算中的误差分析课程.pptx
会计学前言波动方程:波动方程是声学量在声场中满足的基本关系式,反映了波动特征,也是进行声场计算的基本关系式。在导出波动方程前,为了使问题简化,需要对介质和声波做一些假设:(1)介质是均匀连续的,即在波长数量级距离内,介质的声学性质保持不变;(2)介质是理想流体介质,声波在其中传播时没有能量损耗,即忽略介质的粘滞性和热传导性;(3)研究小振幅波的传播规律,所谓小振幅波是指各声学量都是一级小量。波动方程是描述波动运动的数学表达式,它由连续性方程、状态方程和运动方程推导得到。波动方程:理想流体介质中小振幅平面波

计算声学数值计算中的误差分析学习教案.pptx
会计学水声学主要研究声波在水下的辐射、传播与接收,用以解决与水下目标探测和信息传输过程有关的各种声学问题。声波是目前在海洋中唯一能够远距离传播的能量辐射形式。因此作为信息载体的声波,在海洋中所形成的声场时空结构,就成为近代水声学的基本研究内容,而提取海洋中声场信息的结构是我们(wǒmen)用来进行水下探测、识别、通信及环境监测等的手段。前言(qiányán)波动方程:波动方程是声学量在声场中满足的基本关系式,反映了波动特征,也是进行(jìnxíng)声场计算的基本关系式。在导出波动方程前,为了使问题简化,

数值计算中的误差分析与修正方法.pdf
数值计算中的误差分析与修正方法引言:在现代科学和工程领域中,数值计算扮演着至关重要的角色,因为它能够为研究人员和工程师们提供精确、高效的解决复杂问题的手段。然而,由于计算机的本质限制,数值计算常常会引入各种误差,从而影响计算结果的准确性和可靠性。本文将探讨数值计算中常见的误差类型以及相应的分析和修正方法,旨在提高计算结果的精确性。一、误差类型和来源1.舍入误差:舍入误差是由于现代计算机内部对数字表示进行近似导致的。由于计算机使用有限的二进制位数来表示实数,因此无法精确表示一些无理数或十进制小数。这导致在执
第一章数值计算中的误差.ppt
Tel:86613747E-mail:lss@zjtcm.net授课:68学分:4在数学发展中,理论和计算是紧密联系的。现代计算机的出现为大规模的数值计算创造了条件,集中而系统的研究适用于计算机的数值方法变得十分迫切和必要。数值计算方法正是在大量的数值计算实践和理论分析工作的基础上发展起来的,它不仅仅是一些数值方法的简单积累,而且揭示了包含在多种多样的数值方法之间的相同的结构和统一的原理。数值算法是进行科学计算必不可缺少的起码常识;更为重要的是通过对它们的讨论,能够使人们掌握设计数值算法的基本方法和一般原
