matlab在科学计算中的应用.ppt

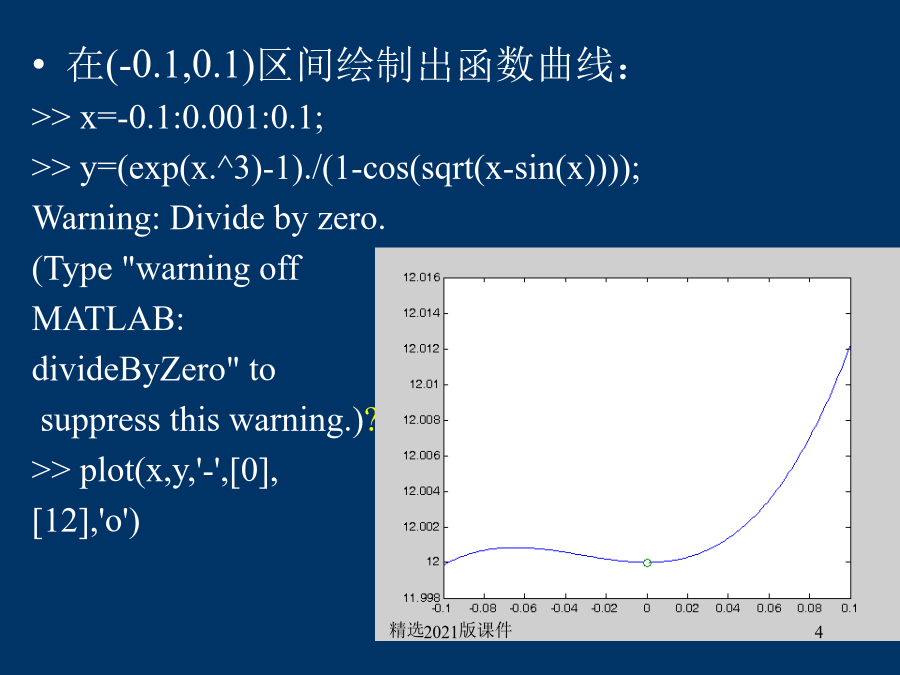
第三章微积分问题的计算机求解3.1微积分问题的解析解3.1.1极限问题的解析解例:试求解极限问题
>>symsxab;
>>f=x*(1+a/x)^x*sin(b/x);
>>L=limit(f,x,inf)
L=
exp(a)*b
例:求解单边极限问题
>>symsx;
>>limit((exp(x^3)-1)/(1-cos(sqrt(x-sin(x)))),x,0,'right')
ans=
12在(-0.1,0.1)区间绘制出函数曲线：
>>x=-0.1:0.001:0.1;
>>y=(exp(x.^3)-1)./(1-cos(sqrt(x-sin(x))));
Warning:Dividebyzero.
(Type"warningoff
MATLAB:
divideByZero"to
suppressthiswarning.)??
>>plot(x,y,'-',[0],
[12],'o')多变量函数的极限：

格式：L1=limit(limit(f,x,x0),y,y0)
或L1=limit(limit(f,y,y0),x,x0)

如果x0或y0不是确定的值，而是另一个变量的函数，如x->g(y)，则上述的极限求取顺序不能交换。例：求出二元函数极限值

>>symsxya;
>>f=exp(-1/(y^2+x^2))…*sin(x)^2/x^2*(1+1/y^2)^(x+a^2*y^2);
>>L=limit(limit(f,x,1/sqrt(y)),y,inf)
L=
exp(a^2)3.1.2函数导数的解析解cos(x)sin(x)(2x+4)
-----------------------------------
222
x+4x+3(x+4x+3)

原函数及一阶导数图：
>>x1=0:.01:5;
>>y=subs(f,x,x1);
>>y1=subs(f1,x,x1);
>>plot(x1,y,x1,y1,‘:’)

更高阶导数：
>>tic,diff(f,x,100);toc
elapsed_time=
4.6860原函数4阶导数
>>f4=diff(f,x,4);pretty(f4)
2
sin(x)cos(x)(2x+4)sin(x)(2x+4)
------------+4--------------------12-----------------
22223
x+4x+3(x+4x+3)(x+4x+3)

3
sin(x)cos(x)(2x+4)cos(x)(2x+4)
+12----------------24-----------------+48----------------
222423
(x+4x+3)(x+4x+3)(x+4x+3)

42
sin(x)(2x+4)sin(x)(2x+4)sin(x)
+24------------------72-----------------+24---------------
252423
(x+4x+3)(x+4x+3)(x+4x+3)多元函数的偏导：

格式：f=diff(diff(f,x,m),y,n)
或f=diff(diff(f,y,n),x,m)

例：求其偏导数并用图表示。

>>symsxyz=(x^2-2*x)*exp(-x^2-y^2-x*y);
>>zx=simple(diff(z,x))
zx=
-exp(-x^2-y^2-x*y)*(-2*x+2+2*x^3+x^2*y-4*x^2-2*x*y)
>>zy=diff(z,y)
zy=
(x^2-2*x)*(-2*y-x)*exp(-x^2-y^2-x*y)
直接绘制三维曲面
>>[x,y]=meshgrid(-3:.2:3,-2:.2:2);
>>z=(x.^2-2*x).*exp(-x.^2-y.^2-x.*y);
>>surf(x,y,z),axis([-33-22-0.71.5])>>contour(x,y,z,30),holdon%绘制等值线
>>zx=-exp(-x.^2-y.^2-x.*y).*(-2*x+2+2*x.^3+x.^2.*y-4*x.^2-2*x.*y);
>>zy=-x.*(x-2).*(2*y+x).*exp(-x.^2-y.^2-x.*y);%偏导的数值解
>>quiver(x,y,zx,zy)%绘制引力线例

>>symsxyz;f=sin(x^2*y)*exp(-x^2*y-z^2);
>>df=diff(diff(diff(f,x,2),y),z);df=simple(df);
>>pretty(df)
22222
-4zexp(-xy-z)(cos(xy)-10cos(xy)yx+4
2422422
sin(x