
轴测投影变换矩阵的研究.docx

快乐****蜜蜂


在线预览结束,喜欢就下载吧,查找使用更方便
相关资料

轴测投影变换矩阵的研究.docx
轴测投影变换矩阵的研究轴测投影变换矩阵的研究1.引言轴测投影是一种在三维空间中将物体投影到二维平面上的技术。这种投影方法能够展示三维物体的形状和结构,并且能够呈现出一些透视效果,使得观察者能够更好地理解物体的尺寸和位置关系。轴测投影广泛应用于建筑设计、工程制图、游戏开发等领域。本论文旨在研究轴测投影的变换矩阵,并探讨其在计算机图形学中的应用。2.轴测投影的基本原理轴测投影是将三维物体投影到一个平面上的过程。常见的轴测投影方法有等轴测投影、二轴测投影和三轴测投影。其中,等轴测投影将物体的三个坐标轴按照相等的
轴测投影图正等轴测图.pptx
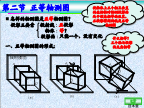
第二节正等轴测图回本节O1A1二、正等轴测图的投影特性常用轴测投影的种类三、正等轴测图的基本作图方法[例1]坐标法画出六棱锥台的正等轴测图F[例2]切割法画出切割体的正等轴测图步骤1/5:步骤2/5:步骤3/5:步骤4/5:步骤5/5:四、正等轴测图中平行于坐标面的圆的轴测投影2、椭圆长短轴的大小水平圆的正等轴测投影水平圆的正等轴测投影4、圆角的画法[例3]试画出图所示立体的正等轴测图。步骤一:步骤二:步骤三:步骤四:小结:本讲结束

斜投影变换及其应用的研究.docx
斜投影变换及其应用的研究斜投影变换及其应用的研究摘要:斜投影变换是一种重要的图像处理技术,可用于改变图像的视角和投影,广泛应用于计算机图形学、计算机辅助设计等领域。本论文将综述斜投影变换的基本原理、常见方法以及其应用的研究进展。通过对不同方法的对比和分析,我们发现斜投影变换在图像处理中具有广泛的应用前景。第一部分:引言斜投影变换是一种将二维图像从一个视角转换到另一个视角的技术。通过斜投影变换,可以改变图像的投影角度和视角,从而产生不同的视觉效果。斜投影变换在计算机图形学、计算机辅助设计、虚拟现实等领域具有

轴测透视.pptx
第三章轴测透视23456二、轴测轴、轴间角、轴向变形系数912§3-3正等轴测投影变形系数简化后所画的轴测图,平行于坐标轴的尺寸都放大了1.22倍,但这对表达形体的直观形象没影响。(1)根据形体结构的特点,选定坐标原点位置。(4)连接A1B1、C1、D1E1、F1,完成顶面正等测轴测图;三种方向正等轴测圆柱的比较圆角是圆的四分之一,其正等测画法与圆的正等测相同,即作出对应的四分之一菱形,画出近似圆弧。四、组合体的正等测作图方法例2画正等测轴测图例3作图(a)曲面立体正等测图。解(1)选取坐标轴,如图(a)

建立绘制轴测图数学模型的研究.pdf
第卷第期福建师范大学学报自然科学版.年月。
