
时域采样与频域采样.docx

快乐****蜜蜂








在线预览结束,喜欢就下载吧,查找使用更方便
相关资料

时域采样与频域采样.docx
实验二:时域采样与频域采样实验目的:时域采样理论与频域采样理论是数字信号处理中的重要理论。要求掌握模拟信号采样前后频谱的变化,以及如何选择采样频率才能使采样后的信号不丢失信息;要求掌握频率域采样会引起时域周期化的概念,以及频率域采样定理及其对频域采样点数选择的指导作用。二、实验原理与方法:1、时域采样定理的要点:1)对模拟信号以间隔T进行时域等间隔理想采样,形成的采样信号的频谱是原模拟信号频谱以采样角频率()为周期进行周期延拓。公式为:2)采样频率必须大于等于模拟信号最高频率的两倍以上,才能使采样信号的频

时域采样与频域采样.doc
实验二:时域采样与频域采样实验目的:时域采样理论与频域采样理论是数字信号处理中的重要理论。要求掌握模拟信号采样前后频谱的变化,以及如何选择采样频率才能使采样后的信号不丢失信息;要求掌握频率域采样会引起时域周期化的概念,以及频率域采样定理及其对频域采样点数选择的指导作用。二、实验原理与方法:1、时域采样定理的要点:1)对模拟信号以间隔T进行时域等间隔理想采样,形成的采样信号的频谱是原模拟信号频谱以采样角频率()为周期进行周期延拓。公式为:2)采样频率必须大于等于模拟信号最高频率的两倍以上,才能使采样信号的频

实验二:时域采样与频域采样.doc
实验二:时域采样与频域采样1.实验目的时域采样理论与频域采样理论是数字信号处理中的重要理论。要求掌握模拟信号采样前后频谱的变化以及如何选择采样频率才能使采样后的信号不丢失信息;要求掌握频率域采样会引起时域周期化的概念以及频率域采样定理及其对频域采样点数选择的指导作用。2.实验原理与方法对模拟信号以间隔T进行时域等间隔理想采样形成的采样信号的频谱是原模拟信号频谱以采样角频率()为周期进行周期延拓。公式为:采样频率必须大于等于模拟信号最高频率的两倍以上才能使采样信号的频谱不产生频谱混叠。实验内容及步骤%

实验二:时域采样与频域采样.doc
实验二:时域采样与频域采样1.实验目的时域采样理论与频域采样理论是数字信号处理中的重要理论。要求掌握模拟信号采样前后频谱的变化以及如何选择采样频率才能使采样后的信号不丢失信息;要求掌握频率域采样会引起时域周期化的概念以及频率域采样定理及其对频域采样点数选择的指导作用。2.实验原理与方法对模拟信号以间隔T进行时域等间隔理想采样形成的采样信号的频谱是原模拟信号频谱以采样角频率()为周期进行周期延拓。公式为:采样频率必须大于等于模拟信号最高频率的两倍以上才能使采样信号的频谱不产生频谱混叠。实验内容及步骤%
时域采样与频域分析.pdf
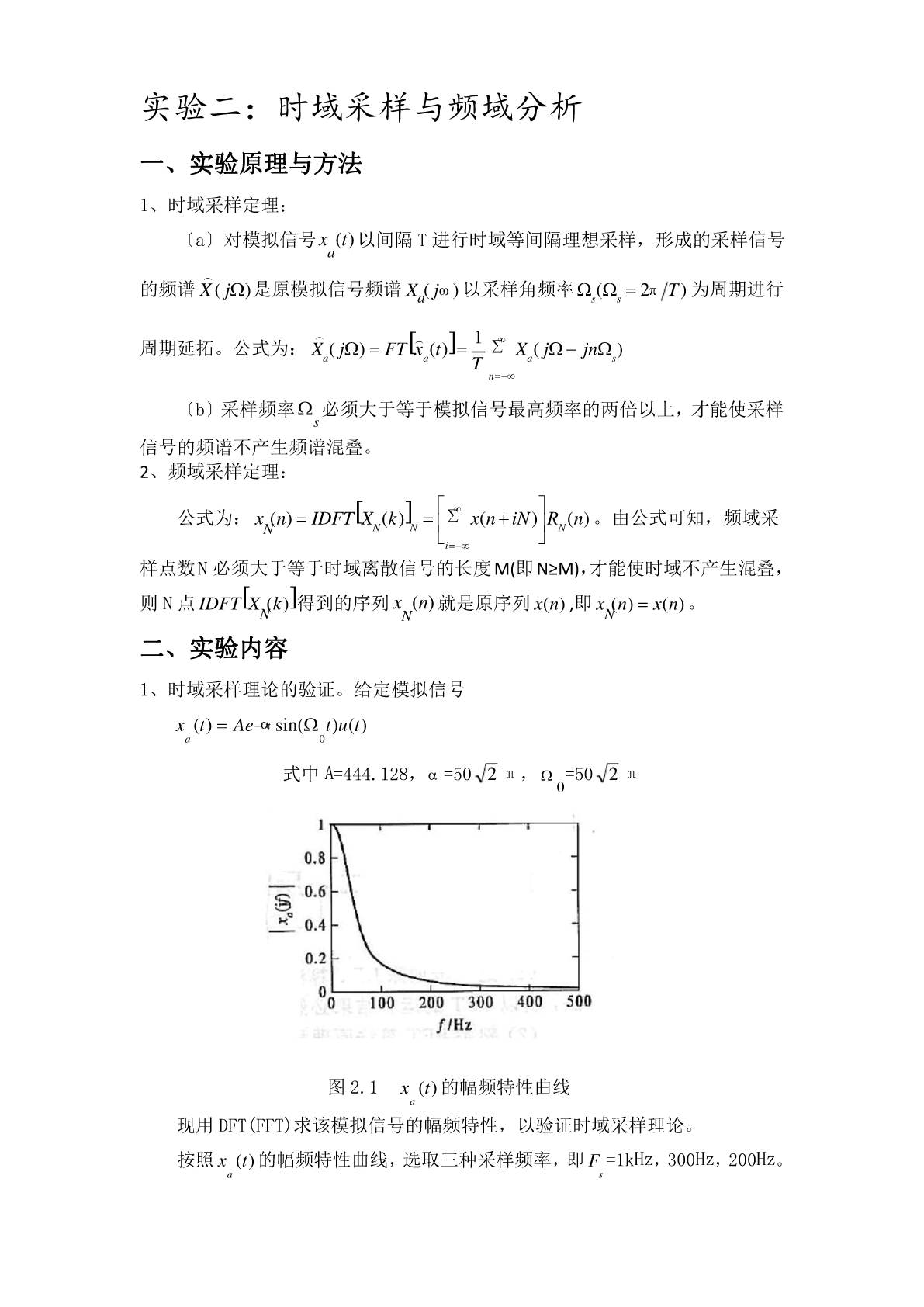
实验二:时域采样与频域分析一、实验原理与方法1、时域采样定理:〔a〕对模拟信号x(t)以间隔T进行时域等间隔理想采样,形成的采样信号a的频谱是原模拟信号频谱X(j)以采样角频率(2T)为周期进行X(j)ass1周期延拓。公式为:X(j)FTx(t)X(jjn)aaTasn〔b〕采样频率必须大于等于模拟信号最高频率的两倍以上,才能使采样s信号的频谱不产生频谱混叠。2、频域采样定理:公式为:x(n)IDFTX(k)x(niN)R(n)。由公式可知
