
离散型随机变量及其分布列ppt课件.ppt

书生****aa









亲,该文档总共32页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

离散型随机变量及其分布列ppt课件.ppt
离散型随机变量及其分布列.引例:(1)抛掷一枚骰子,可能出现的点数有几种情况?(2)姚明罚球2次有可能得到的分数有几种情况?(3)抛掷一枚硬币,可能出现的结果有几种情况?思考:在上述试验开始之前,你能确定结果是哪一种情况吗?在前面的例子中,我们把随机试验的每一个结果都用一个确定的数字来表示,这样试验结果的变化就可看成是这些数字的变化。若把这些数字当做某个变量的取值,则这个变量就叫做随机变量,常用X、Y、x、h来表示。按照我们的定义,所谓的随机变量,就是随机试验的试验结果与实数之间的一个对应关系。那么,随机

离散型随机变量及其分布列ppt课件.ppt
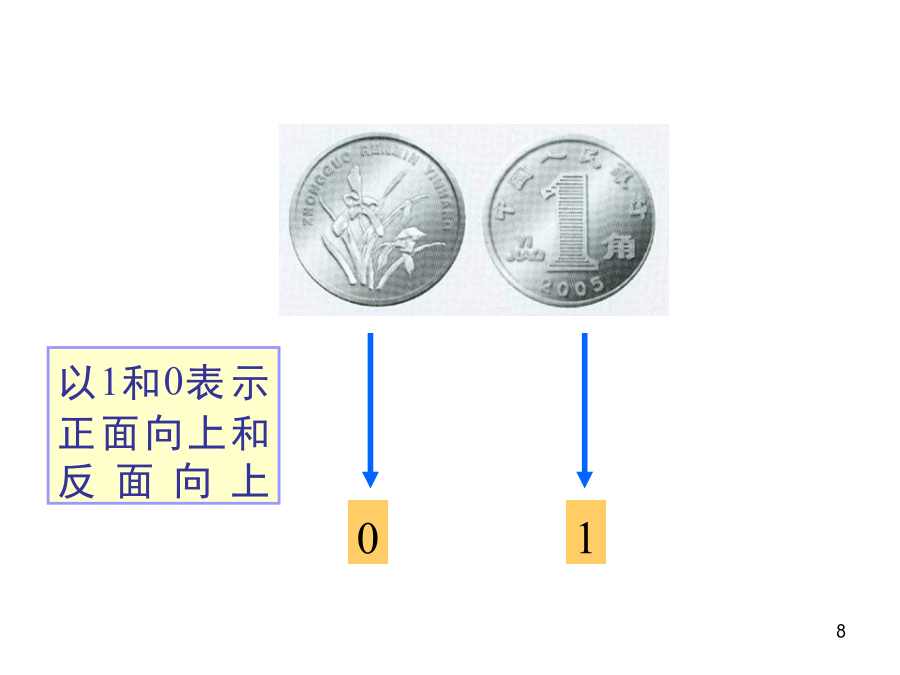
2.1.1离散型随机变量引例:(1)抛掷一枚骰子,可能出现的点数有几种情况?(2)篮球比赛中罚球2次有可能得到的分数有几种情况?(3)抛掷一枚硬币,可能出现的结果有几种情况?思考:在上述试验开始之前,你能确定结果是哪一种情况吗?在前面的例子中,我们把随机试验的每一个结果都用一个确定的数字来表示,这样试验结果的变化就可看成是这些数字的变化。若把这些数字当做某个变量的取值,则这个变量就叫做随机变量,常用X、Y、x、h来表示。1.将一颗均匀骰子掷两次,不能作为随机变量的是()正面朝上反面朝上思考:随机变量与函数

离散型随机变量及其分布列ppt课件.ppt
2.1.1离散型随机变量23某人射击一次,可能出现命中0环,命中1环,…,命中10环等结果,复习回顾:1.事件:必然事件,不可能事件,随机事件2.基本事件特点:①任何两个基本事件都是互斥的②任何事件(除不可能事件)都可以表示成基本事件的和3.随机试验特点:(事实上,“试验”一词有十分广泛的含义:凡是对对象的观察或为此而进行的实验都称之为试验。)①试验的所有可能结果可以事先知道②任何一次试验的确定结果无法事先知道③可以在同一条件下重复作此实验4.古典概型:①有限性②等可能性几何概型:①无限性②等可能性出现的

离散型随机变量及其分布列ppt课件.ppt
2.1.1离散型随机变量23某人射击一次,可能出现命中0环,命中1环,…,命中10环等结果,复习回顾:1.事件:必然事件,不可能事件,随机事件2.基本事件特点:①任何两个基本事件都是互斥的②任何事件(除不可能事件)都可以表示成基本事件的和3.随机试验特点:(事实上,“试验”一词有十分广泛的含义:凡是对对象的观察或为此而进行的实验都称之为试验。)①试验的所有可能结果可以事先知道②任何一次试验的确定结果无法事先知道③可以在同一条件下重复作此实验4.古典概型:①有限性②等可能性几何概型:①无限性②等可能性出现的

离散型随机变量及其分布列ppt课件学习.pptx
会计学一.随机事件:在一定条件下可能发生也可能不发生的事件几点说明:(1)求一个事件的概率的基本方法是通过大量的重复试验(2)概率可看作频率在理论上的期望值,它从数量上反映了随机事件发生的可能性的大小,频率在大量重复试验的前提下可近似地作为这个事件的概率(3)必然事件的概率为1,不可能事件的概率为0,因此一个试验如果满足下述条件:(1)试验可以在相同的条件下重复进行;(2)试验的所有结果是明确的且不止一个;(3)每次试验总是出现这些结果中的一个,但在试验之前却不能肯定这次试验会出现哪一个结果。这样的试验就
