
常用坐标计算及公路路线坐标计算.docx

快乐****蜜蜂






在线预览结束,喜欢就下载吧,查找使用更方便
相关资料

常用坐标计算及公路路线坐标计算.docx
坐标中线测量与计算采用全站仪测量线路中线,其基本的原理就是:利用假定坐标系或大地坐标系,测量各交点的坐标,并计算中线上的任意一点的坐标,利用坐标放样的原理,把各中桩在地面上确定(打桩),以备后续测量。第一节控制点测设由于线路通常较长,为确保测量各交点坐标的准确性,通常在线路的全长,每隔一定的距离设置一个坐标控制点,该控制点的坐标是测量该段线路交点的坐标基准点。因此,坐标中线测量的第一步就是进行控制点的测量。图5-1一、控制点的布设控制点布置在线路沿线两侧,点位尽量放置在较高的位置上,能够看见越长的线路越好

路线中桩坐标计算.pdf
.路线逐桩坐标计算高等级公路路线设计中必须计算各点位的逐桩坐标以作为路线施工放样的依据也是公路交工和峻工验收时检测中线偏位的依据故坐标计算能力已是道路桥梁工程技术专业学生的必备技能。1、路线交点偏角、交点间距、曲线要素及主点桩计算如图所示设路线起点坐标JD(XJYJ
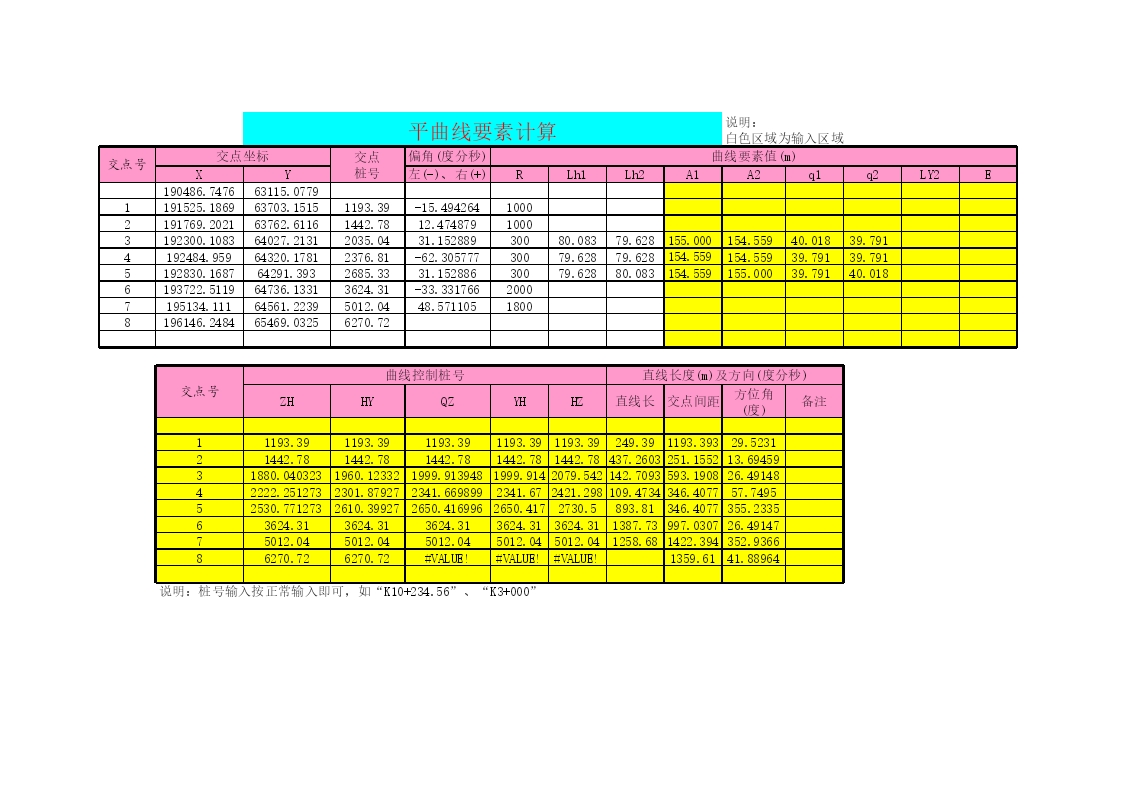
公路坐标计算程序.xls
边桩放样(坡口线或坡脚线)说明:白色区域为输入区域测量数据假定中桩桩号对应中桩桩号左边桩右边桩XYZ距离(S)XLYLSXR说明:桩号输入按正常输入即可,如“K10+234.56”、“K3+000”
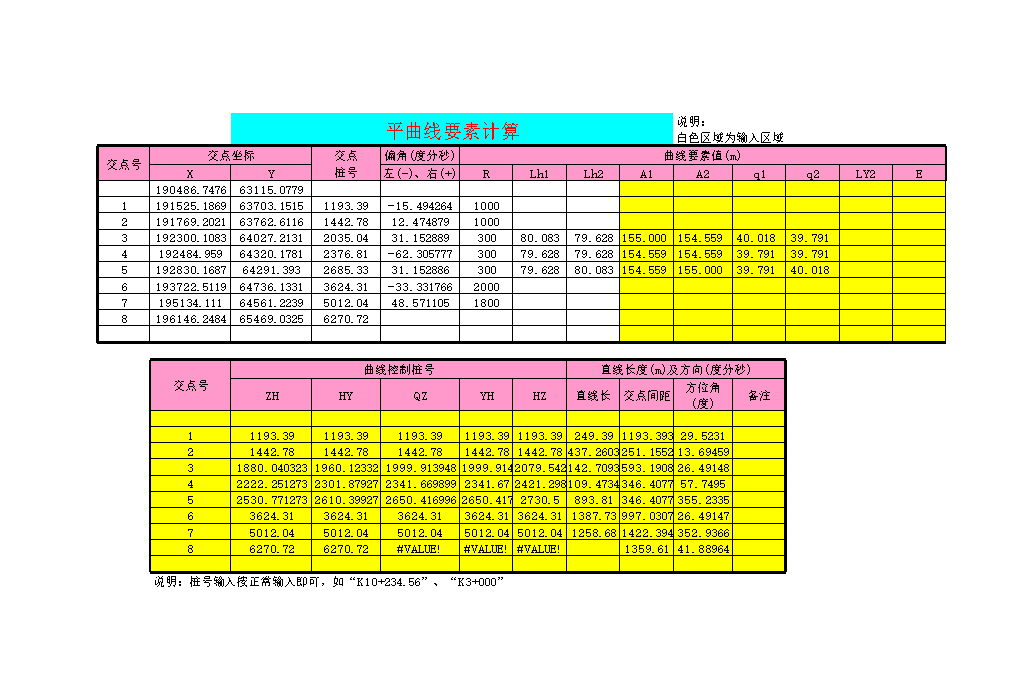
公路坐标计算程序.xls
边桩放样(坡口线或坡脚线)说明:白色区域为输入区域测量数据假定中桩桩号对应中桩桩号左边桩右边桩XYZ距离(S)XLYLSXR说明:桩号输入按正常输入即可,如“K10+234.56”、“K3+000”

路线中线桩点的坐标计算.docx
路线中线桩点的坐标计算如图1所示,已知两交点的坐标:JDi(XJDi,YJDi),JDi-1(XJDi-1,YJDi-1)。路线导线的坐标的坐标方位角A和边长S可按坐标反算公式求得:Ai-1,i=tg-1,(式1)Si-1,i==(式2)Si-1,i=(式3)在选定各圆曲线半经R和缓和曲线长度Ls后,根据各桩点的里程桩号,即可算出相应的坐标值X,Y。HZ点(包括线路起点)至ZH点之间的中桩坐标如图1所示,此段为直线。桩点的坐标按下式计算:XJDi=XHZi-1+DicosAi-1,iYJDi=YHZi-1
