
基于弧齿锥齿轮的四阶传动误差曲线设计方法.pdf

宛菡****魔王










亲,该文档总共17页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

基于弧齿锥齿轮的四阶传动误差曲线设计方法.pdf
本发明公开了一种基于弧齿锥齿轮的四阶传动误差曲线设计方法,用于解决现有四阶传动误差曲线设计方法存在换齿冲击的技术问题。技术方案是将传动误差方程在齿面参考点处按Taylor级数展开成四阶形式,从四阶Taylor级数展开式方程中分离出小轮相对于参考点啮合时转角的表达式,建立拟合二阶曲线的目标函数。建立控制峰峰值之间差距的目标函数,使得当前齿传动误差曲线向左或向右平移一个小轮齿距的距离时,刚好得到先导齿和后继齿的传动误差曲线,即此时相邻两传动误差曲线峰峰之间的距离为一个小轮齿距的距离,交点刚好落在极大值点,使交

一种弧齿锥齿轮的四阶传动误差曲线及其设计方法.pdf
本发明提出了一种性能更加优异的四阶传动误差曲线及其设计方法,这种四阶传动误差曲线在相邻两条曲线之间只有一个交点,减少了换齿次数,降低了冲击和振动频率,且相邻两条曲线在交点处的斜率极为接近,使得换齿时的振动和冲击很小,进一步提高弧齿锥齿轮的传动性能。通过设置预控点,并结合四阶传动误差计算式,确定四阶多项式中各项的系数;按照最大函数值点将曲线向下平移到零线上;将传动误差曲线向左和向右平移一个小轮齿距角,得到前一对齿和后一对齿的传动误差曲线,观察相邻两条传动误差曲线的交点数目和交点处曲线的斜率差,同时调整预控点
一种同步运动传动误差曲线的设计方法及应用传动误差曲线的弧齿锥齿轮.pdf
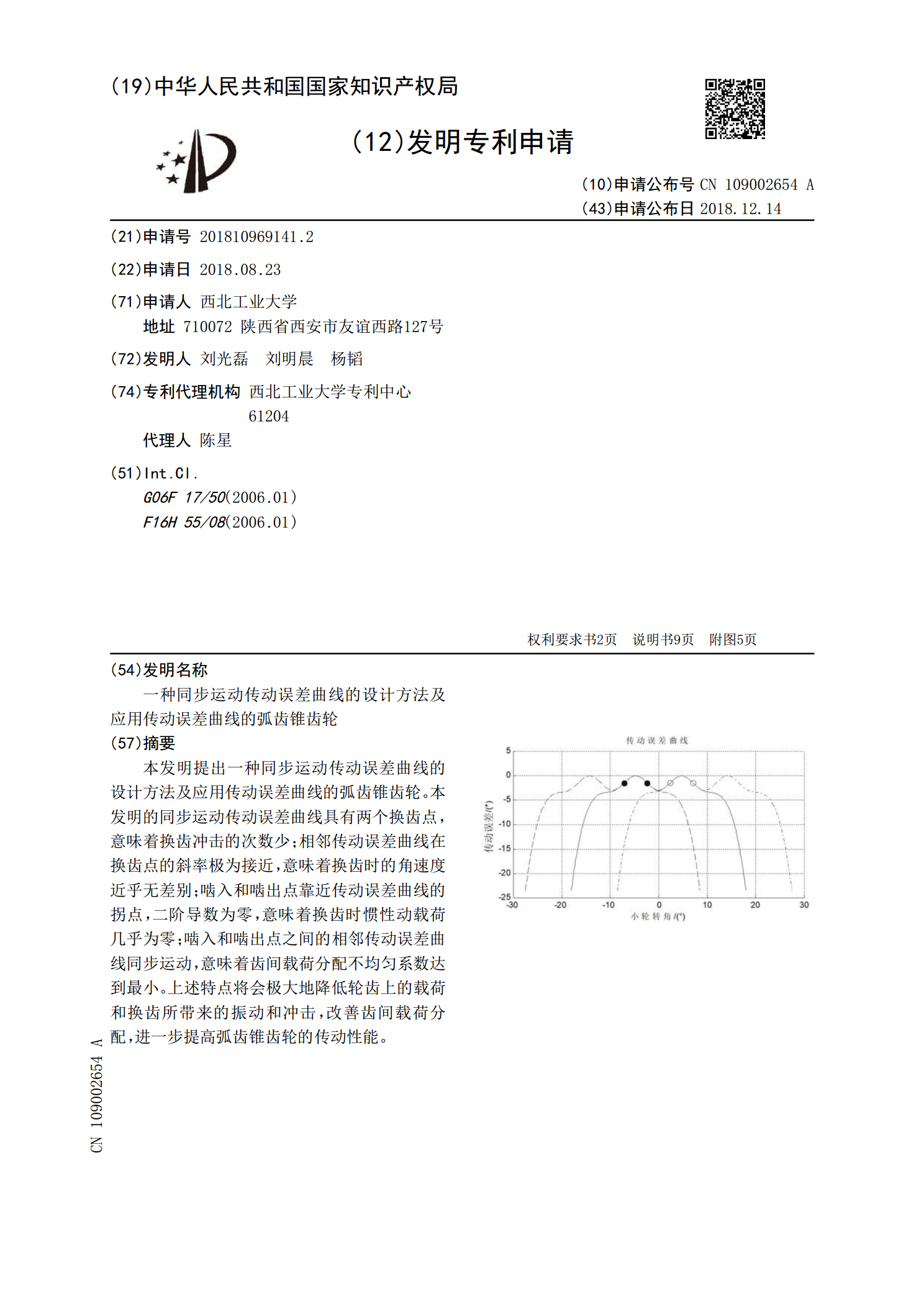
本发明提出一种同步运动传动误差曲线的设计方法及应用传动误差曲线的弧齿锥齿轮。本发明的同步运动传动误差曲线具有两个换齿点,意味着换齿冲击的次数少;相邻传动误差曲线在换齿点的斜率极为接近,意味着换齿时的角速度近乎无差别;啮入和啮出点靠近传动误差曲线的拐点,二阶导数为零,意味着换齿时惯性动载荷几乎为零;啮入和啮出点之间的相邻传动误差曲线同步运动,意味着齿间载荷分配不均匀系数达到最小。上述特点将会极大地降低轮齿上的载荷和换齿所带来的振动和冲击,改善齿间载荷分配,进一步提高弧齿锥齿轮的传动性能。

一种弧齿锥齿轮复合传动误差设计方法.pdf
本发明公开一种弧齿锥齿轮复合传动误差设计方法。该方法从齿坯参数和机床加工参数中,计算出齿轮副在关键设计点的小轮转角和传动误差幅值。确定一个啮合周期内的简谐函数表达式,满足在进入啮合转换点、设计参考点和退出啮合转换点的传动误差要求;分别计算简谐函数两侧传动误差曲线的高阶抛物线表达式,从而形成复合传动误差设计。在小轮加工过程中,通过改变滚比系数,使得齿轮副按照预置的复合传动误差曲线进行啮合传动;采用逆轮齿接触分析方法,获得离散后的小轮滚比系数和摇台转角,再拟合出基本滚比和高阶变性系数,最终实现复合传动误差函数

航空弧齿锥齿轮承载传动误差的分析与设计.docx
航空弧齿锥齿轮承载传动误差的分析与设计航空弧齿锥齿轮承载传动是指由两个同轴的弧齿锥齿轮通过啮合,传递扭矩和转速的机械传动。这种传动具有结构紧凑,重量轻、扭矩传递效率高等优点,因此被广泛应用于航空领域。但是,由于制造和安装误差、结构变形以及摩擦等因素的影响,使得弧齿锥齿轮传动系统存在误差。这些误差会导致传动效率下降、噪声增强甚至传动故障。因此,对弧齿锥齿轮承载传动误差进行分析和设计具有重要意义。一、弧齿锥齿轮承载传动误差分析1.制造和安装误差制造和安装误差是影响弧齿锥齿轮精度的主要因素,具体表现为几何误差和
