
数字信号最佳接收.ppt

my****25









亲,该文档总共39页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

数字信号最佳接收.ppt
8.1匹配滤波器8.2最小差错概率接收准则8.3确知信号的最佳接收机8.4随相信号的最佳接收机8.5最佳接收机性能比较8.6最佳基带传输系统第8章数字信号的最佳接收8.1匹配滤波器(MatchedFilter)在数字信号接收中,滤波器的作用有两个方面,第一是使滤波器输出有用信号成分尽可能强;第二是抑制信号带外噪声,使滤波器输出噪声成分尽可能小,减小噪声对信号判决的影响。通常对最佳线性滤波器的设计有两种准则:一种是使滤波器输出的信号波形与发送信号波形之间的均方误差最小,由此而导出的最佳线性滤波器

数字信号的最佳接收.ppt
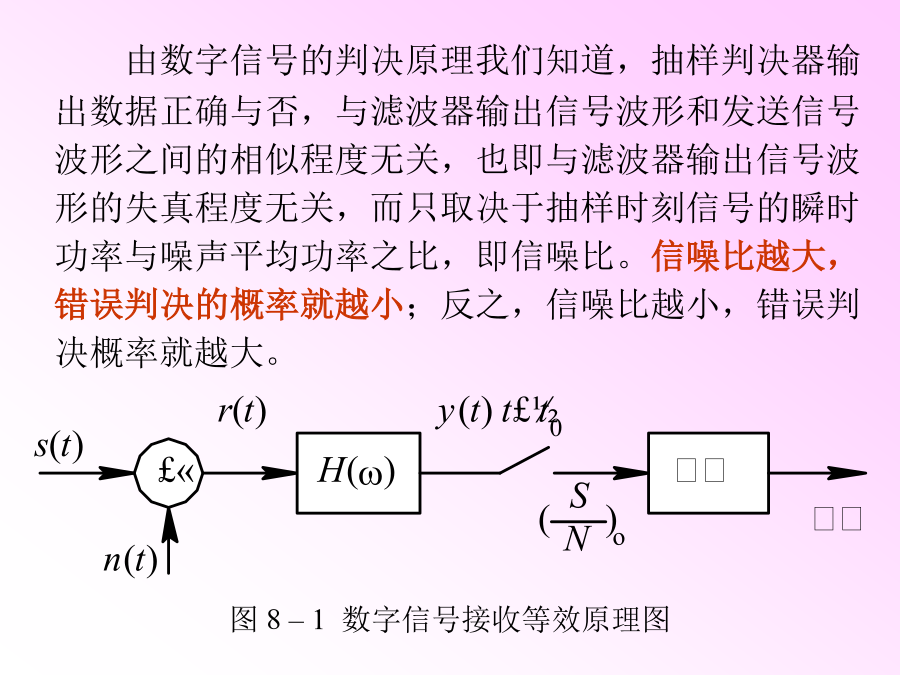
教学提示第八章数字信号的最佳接收8.1引言8.2数字信号接收的统计表述8.3关于最佳接收的准则8.4确知信号的最佳接收S1(t)的相关器S1(t)a(t)b(t)S2(t)S2(t)的相关器二、二进制确知信号最佳接收机的抗噪性能等能量2.s2(t)=0y(t)x(t)r(t)cp(t)四、M进制信号的最佳接收机1.2FSK随相信号的最佳接收若收端提取的两个载波仅与发载波同频但不同相,则2FSK信号为随相信号。设cosω1t、cosω2t正交,,且φ1、φ2在(0,2π)内均匀分布,则最佳接收机形式为8.6

数字信号的最佳接收(5).pptx
通信原理通信原理第10章数字信号最佳接收第10章数字信号最佳接收第10章数字信号最佳接收第10章数字信号最佳接收第10章数字信号最佳接收第10章数字信号最佳接收第10章数字信号最佳接收第10章数字信号最佳接收第10章数字信号最佳接收第10章数字信号最佳接收第10章数字信号最佳接收第10章数字信号最佳接收第10章数字信号最佳接收第10章数字信号最佳接收第10章数字信号最佳接收第10章数字信号最佳接收第10章数字信号最佳接收第10章数字信号最佳接收第10章数字信号最佳接收第10章数字信号最佳接收第10章数字信

数字信号的最佳接收(1).pptx
2024/4/82345678910112024/4/81314151617181920212223242526272829303132333435363738

数字信号最佳接收原理.pptx
第8章数字信号最佳接收本章内容目的要求基本概念的认识数字信号的最佳接收:从噪声的干扰中,判决有用信号是否出现,属于假设检验。参数估计:从噪声的干扰中对信号的参数进行估计。最佳:是在某种准则之下达到的最优。观测空间对x(t)进行N次观测得到:种错误是假设H0时,而X落在z1判决域内,也称为虚报告概率第二种错误是假设H1时,而X落在z0判决域内,也称为漏报告概率平均错误概率:x0就是最佳判决门限,由此可以得到判决规则还可以简写为:进一步则可先任意选择判决点x0,求出此时的平均风险,然后对x0求导,并令导数等于
