
结构力学极限荷载.pptx

my****25








亲,该文档总共64页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

结构力学极限荷载.pptx
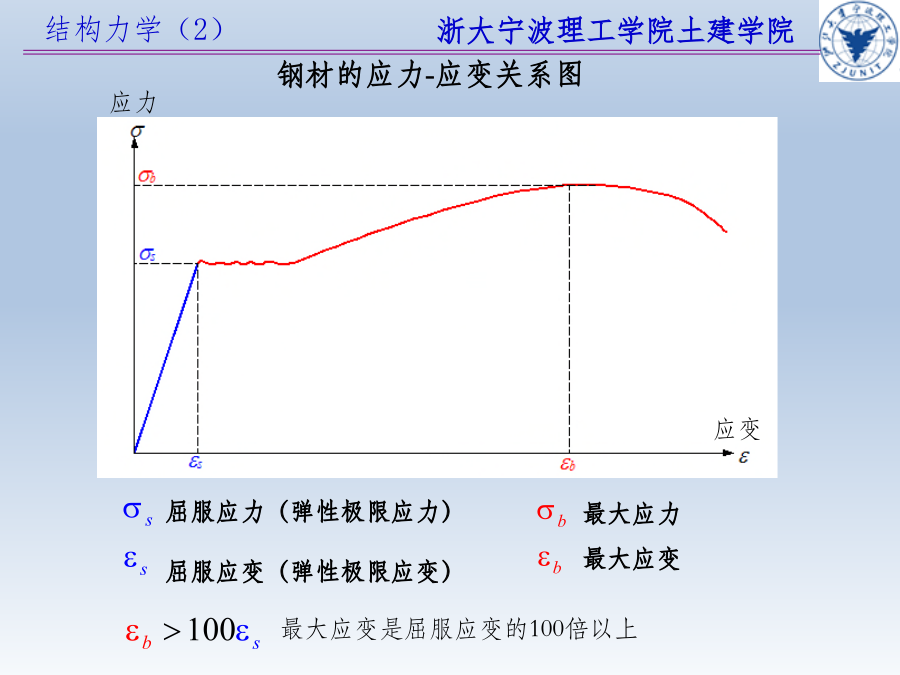
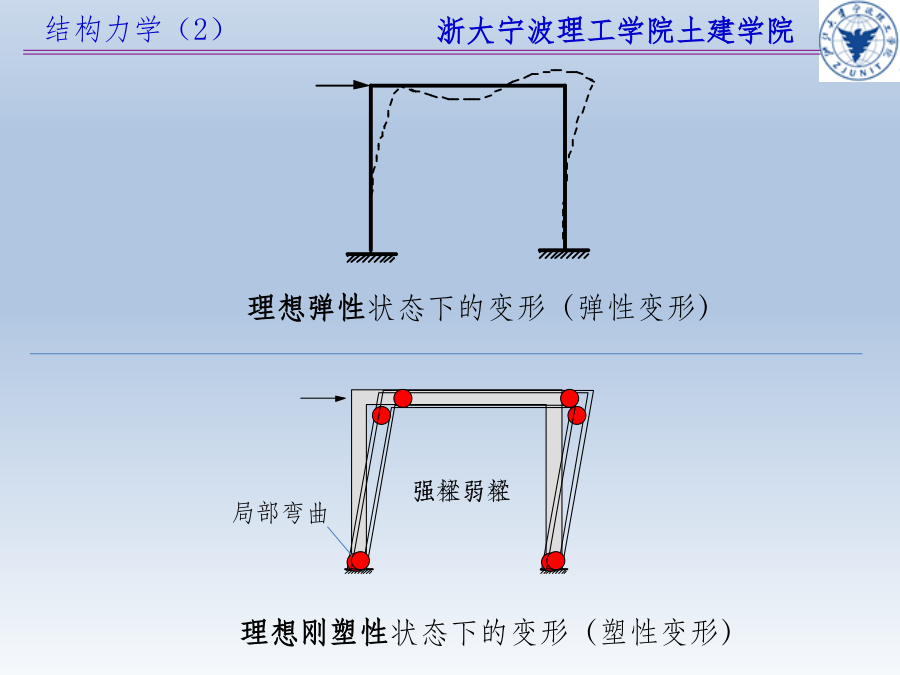
会计学弹性设计法(许用应力法)弹性设计例弹性变形屈服应力(弹性极限应力)屈服应变(弹性极限应变)钢材的应力-应变关系图屈服应力yieldstress(弹性阶段最大应力)屈服应变yieldstrain(弹性阶段最大应变)理想弹性状态下的变形(弹性变形)极限状态下构件的变形理想弹性状态下的变形(弹性变形)塑性铰基本假设(一般针对钢材料)1、材料为“理想弹塑性材料”。2、材料均匀,各向同性。3、平面假定。即无论弹、塑性阶段,都保持平截面不变。塑性设计法的要点1.计算极限荷载2.极限荷载除以荷载安全系数得出容许荷

结构力学极限荷载.pptx
结构力学(2)弹性设计:利用弹性计算的结果,以许用应力为依据来确定截面尺寸或进行强度验算的设计法。在计算中假设应力与应变为线性关系,结构在卸载后没有残余变形。其特点是通过计算弹性阶段各杆件最大应力的方法进行强度验算,确保不超过许用应力。塑性设计:先确定结构破坏时所能承受的荷载(极限荷载),然后将极限荷载除以荷载系数得到容许荷载并进行设计。其特点是通过计算极限荷载的方式确定结构破坏时所能承受的荷载。弹性设计法(许用应力法)弹性设计例弹性变形屈服应力(弹性极限应力)屈服应变(弹性极限应变)钢材的应力-应变关系

结构力学教程 结构的极限荷载.ppt
结构的极限荷载1.极限荷载、强度条件和计算假定计算假定:1.弹性阶段2.弹塑性阶段极限弯矩与外力无关,只与材料的物理性质和截面几何形状、尺寸有关。极限弯矩与外力无关,只与材料的物理性质和截面几何形状、尺寸有关。塑性铰破坏机构3.静定结构的极限荷载例:已知屈服应力为。求极限荷载。4.单跨超静定梁的极限荷载从受力情况,可判断出塑性铰发生的位置应为A、C。利用极限状态的平衡可直接求出极限荷载。例:求图示等截面梁的极限荷载.已知梁的极限弯矩为Mu。例:求图示变截面梁的极限荷载.已知AB段的极限弯矩为2Mu,BC段

结构力学教学-12结构的极限荷载.pptx
Dec.2013概述极限弯矩和塑性铰静定梁的极限荷载;单跨超静定梁的极限荷载;比例加载的一般定理及应用弹性设计方法:荷载卸去后,结构会恢复到原来形状无任何残余变形。(不能充分估计结构屈服后承载力,偏于保守和不经济)塑性设计方法:以结构破坏时的荷载作为标准(承载力不再增加)极限荷载分析假定:塑性铰结构由于出现塑性铰而形成的机构称为破坏机构。静定结构无多余约束,出现一个塑性铰即成为破坏机构。这时结构上的荷载即为极限荷载。例:求图示等截面梁的极限荷载.已知梁的极限弯矩为Mu。由前面例题可见:若分析出塑性铰的位置

梁和刚架的极限荷载结构力学.ppt
结构力学第15章梁和刚架的极限荷载s15.2极限弯矩、塑性铰、破坏机构3、截面形状系数:极限弯矩与屈服弯矩之比二、塑性铰三、破坏机构由于足够多的塑性铰的出现,使原结构成为机构(几何可变体系),失去继续承载的能力,该几何可变体系称为“机构”。四、如何确定单跨梁的极限荷载2、确定单跨梁极限荷载的机动法3、确定单跨梁极限荷载的静力法4、确定复杂结构极限荷载面临的问题试确定图示单跨梁的极限荷载2、小变形假设(几何线形),变形后仍用变形前的几何尺寸。2、屈服条件当荷载达到极限值时,结构上各截面的弯矩都不能超过其极
