
连续时间周期信号频域分析的MATLAB实现.docx

快乐****蜜蜂



在线预览结束,喜欢就下载吧,查找使用更方便
相关资料

连续时间周期信号频域分析的MATLAB实现.docx
连续时间周期信号频域分析的MATLAB实现频域分析是一种重要的信号处理技术,用于研究信号在频域上的特性。在频域分析中,我们可以将一个连续时间周期信号转换为该信号的频谱表示,以了解信号的频率内容和频域特性。本文将介绍如何使用MATLAB实现连续时间周期信号的频域分析。1.连续时间周期信号的定义连续时间周期信号是在连续时间域上具有周期性的信号。数学上,连续时间周期信号可以表示为:x(t)=x(t+T)其中,T表示信号的周期。在频域分析中,我们将关注信号在一个周期内的频率内容。2.连续时间周期信号的频谱表示连续

第7章 周期信号频域分析及 MATLAB 实现.ppt
第七章信号频域分析及MATLAB实现7.1周期信号的傅里叶级数与信号的频谱7.1周期信号的傅里叶级数与信号的频谱7.1周期信号的傅里叶级数与信号的频谱7.1周期信号的傅里叶级数与信号的频谱7.1周期信号的傅里叶级数与信号的频谱7.1周期信号的傅里叶级数与信号的频谱7.2Matlab分析周期信号的频谱7.2.2单边频谱分析例题7.1周期矩形脉冲信号幅度为1,脉宽为1,周期为4,求该信号的三角形式的其各阶傅里叶系数,并绘出各次谐波叠加的傅里叶综合波形图。2.绘制函数图例题的理论推算调用SquarePulse计

连续时间信号的频域分析.doc
实验二连续时间信号的频域分析实验内容:1、周期信号的傅里叶级数与GIBBS现象给定如一个周期信号如图所示:Q2-1:分别手工计算x1(t)的傅里叶级数的系数。信号x1(t)在其主周期内的数学表达式为:计算x1(t)的傅里叶级数的系数的计算过程如下:解:首先,我们根据前面所给出的公式,计算该信号的傅里叶级数的系数。()在MATLAB命令窗口,依次键入:>>k=-10:10;>>ak=sin(0.2*(k+eps)*pi)./((k+eps)*pi)用MATLAB帮助你计算出你手工计算的傅里叶级数的系数ak从
连续时间信号与系统的频域分析.ppt
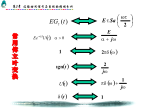
常用傅立叶变换3.5连续时间系统的频域分析一、系统函数(传输函数):1、定义:2、求法:1)从定义求;2)从方程求;3)从冲激响应求;.4)从系统框图求;5)从电路图求.例:求系统函数H(j)。二、系统零状态响应:三、系统频率特性:MATLAB的计算机仿真:四、非周期信号激励下系统的零状态响应解题步骤例:五、系统全响应:六、周期信号通过线性系统2、正弦信号:3、任意周期信号:例:图示系统,若激励如图所示,求响应i(t)。练习:图示系统,频率特性如图所示,求响应y(t)。其中

连续时间信号的频域分析[1].doc
1symstwf1=sin(t);Fw1=fourier(f1)f2=sin(t)/t;Fw2=fourier(f2)f3=sym('Heaviside(t+1)-Heaviside(t-1)';Fw3=fourier(f3)f4=sym('Heaviside(t)');Fw4=fourier(f4)f5=sym(1);Fw5=fourier(f5)f6=exp(-2*abs(t));Fw6=fourier(f6)运行得:Fw1=i*pi*(-dirac(w-1)+dirac(w+1))Fw2=pi*(-
