
连续时间信号的频域分析.doc

as****16







在线预览结束,喜欢就下载吧,查找使用更方便
相关资料

连续时间信号的频域分析.doc
实验二连续时间信号的频域分析实验内容:1、周期信号的傅里叶级数与GIBBS现象给定如一个周期信号如图所示:Q2-1:分别手工计算x1(t)的傅里叶级数的系数。信号x1(t)在其主周期内的数学表达式为:计算x1(t)的傅里叶级数的系数的计算过程如下:解:首先,我们根据前面所给出的公式,计算该信号的傅里叶级数的系数。()在MATLAB命令窗口,依次键入:>>k=-10:10;>>ak=sin(0.2*(k+eps)*pi)./((k+eps)*pi)用MATLAB帮助你计算出你手工计算的傅里叶级数的系数ak从
连续时间信号与系统的频域分析.ppt
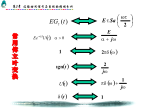
常用傅立叶变换3.5连续时间系统的频域分析一、系统函数(传输函数):1、定义:2、求法:1)从定义求;2)从方程求;3)从冲激响应求;.4)从系统框图求;5)从电路图求.例:求系统函数H(j)。二、系统零状态响应:三、系统频率特性:MATLAB的计算机仿真:四、非周期信号激励下系统的零状态响应解题步骤例:五、系统全响应:六、周期信号通过线性系统2、正弦信号:3、任意周期信号:例:图示系统,若激励如图所示,求响应i(t)。练习:图示系统,频率特性如图所示,求响应y(t)。其中

连续时间信号的频域分析[1].doc
1symstwf1=sin(t);Fw1=fourier(f1)f2=sin(t)/t;Fw2=fourier(f2)f3=sym('Heaviside(t+1)-Heaviside(t-1)';Fw3=fourier(f3)f4=sym('Heaviside(t)');Fw4=fourier(f4)f5=sym(1);Fw5=fourier(f5)f6=exp(-2*abs(t));Fw6=fourier(f6)运行得:Fw1=i*pi*(-dirac(w-1)+dirac(w+1))Fw2=pi*(-

连续时间信号的频域分析(信号与系统课设)综述.pdf
福建农林大学计算机与信息学院信息工程类课程设计报告课程名称:信号与系统课程设计题目:连续时间信号的频域分析姓名:系:电子信息工程专业:电子信息工程年级:2008学号:指导教师:职称:2011年1月10日1福建农林大学计算机与信息学院信息工程类课程设计结果评定评语:成绩:指导教师签字:任务下达日期:评定日期:2目录1课程设计的目的………………………………………………………………12课程设计的要求………………………………………………………………13课程设计报告内容……………………………………………………………

连续时间信号的频域分析(信号与系统课设)综述.pdf
福建农林大学计算机与信息学院信息工程类课程设计报告课程名称:信号与系统课程设计题目:连续时间信号的频域分析姓名:系:电子信息工程专业:电子信息工程年级:2008学号:指导教师:职称:2011年1月10日1福建农林大学计算机与信息学院信息工程类课程设计结果评定评语:成绩:指导教师签字:任务下达日期:评定日期:2目录1课程设计的目的………………………………………………………………12课程设计的要求………………………………………………………………13课程设计报告内容……………………………………………………………
