
求解无限长载流直螺线管磁场的两种方法比较研究.docx

快乐****蜜蜂


在线预览结束,喜欢就下载吧,查找使用更方便
相关资料

求解无限长载流直螺线管磁场的两种方法比较研究.docx
求解无限长载流直螺线管磁场的两种方法比较研究无限长载流直螺线管磁场的求解是电磁学中的一个经典问题,这个问题涉及到许多物理概念和数学方法,是电磁学研究的基础之一。在实际应用中,我们需要了解不同方法求解无限长载流直螺线管磁场的优缺点,以便更好地应用于各种场合。方法一:安培环定理安培环定理是求解电流所产生的磁场的一种重要方法。在求解无限长载流直螺线管的磁场时,我们可以使用安培环定理来快速求解。根据安培环定理,我们可以得到任意形状的回路上磁场的积分等于其内部的总电流。对于一个无限长载流直螺线管,我们可以把一段环绕

载流长直导线的磁场.ppt
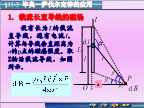
1.载流长直导线的磁场所有dB的方向相同,所以P点的的大小为:由几何关系有:考虑三种情况:2.载流圆线圈轴线上的磁场各电流元的磁场方向不相同,可分解为和,由于圆电流具有对称性,其电流元的逐对抵消,所以P点的大小为:载流圆线圈轴线上的磁场(1)在圆心处3.载流直螺线管内部的磁场由于每匝可作平面线圈处理,ndl匝线圈可作Indl的一个圆电流,在P点产生的磁感应强度:R讨论:例一个半径R为的塑料薄圆盘,电量+q均匀分布其上,圆盘以角速度绕通过盘心并与盘面垂直的轴匀速转动。求圆盘中心处的磁感应强度。例题11-1
载流长直导线的磁场(1).ppt
1.载流长直导线的磁场所有dB的方向相同,所以P点的的大小为:由几何关系有:考虑三种情况:2.载流圆线圈轴线上的磁场各电流元的磁场方向不相同,可分解为和,由于圆电流具有对称性,其电流元的逐对抵消,所以P点的大小为:载流圆线圈轴线上的磁场(1)在圆心处3.载流直螺线管内部的磁场由于每匝可作平面线圈处理,ndl匝线圈可作Indl的一个圆电流,在P点产生的磁感应强度:R讨论:例一个半径R为的塑料薄圆盘,电量+q均匀分布其上,圆盘以角速度绕通过盘心并与盘面垂直的轴匀速转动。求圆盘中心处的磁感应强度。例题11-1

无限长螺线管内外磁场研究.docx
无限长螺线管内外磁场研究无限长螺线管内外磁场研究摘要:无限长螺线管是物理中常用的一种电磁设备,对其内外磁场进行研究可以帮助我们更好地理解电磁感应现象以及磁场的分布规律。本文将探讨无限长螺线管内外的磁场特性,通过理论分析和计算得出了其分布规律,并与实验结果进行比较,验证了理论的准确性。关键词:无限长螺线管,磁场,电磁感应,分布规律引言:无限长螺线管是由导线绕成的螺旋形结构,当通电时,会在螺线管内外产生磁场。研究无限长螺线管内外磁场的特性,对于理解电磁感应现象、设计电磁设备等都具有重要意义。一、理论分析1.1

无限长直密绕通电螺线管磁场的一种简单计算方法.docx
无限长直密绕通电螺线管磁场的一种简单计算方法无限长直密绕通电螺线管磁场的一种简单计算方法摘要:本论文介绍了一种简单计算无限长直密绕通电螺线管磁场的方法,通过建立数学模型,利用安培定理和比奥萨伐尔定律,推导出磁场的表达式,并通过模拟实验验证了该方法的有效性。引言:无限长直密绕通电螺线管是一种常见的电磁装置,应用广泛。研究其磁场分布不仅有助于深入了解其物理本质,而且还有助于优化装置设计和应用。传统的计算无限长直密绕通电螺线管磁场的方法常常比较复杂,需要大量的数学推导和计算,因此需要一种简单而有效的计算方法。方
