
载流长直导线的磁场(1).ppt

仙人****88






亲,该文档总共21页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料
载流长直导线的磁场(1).ppt
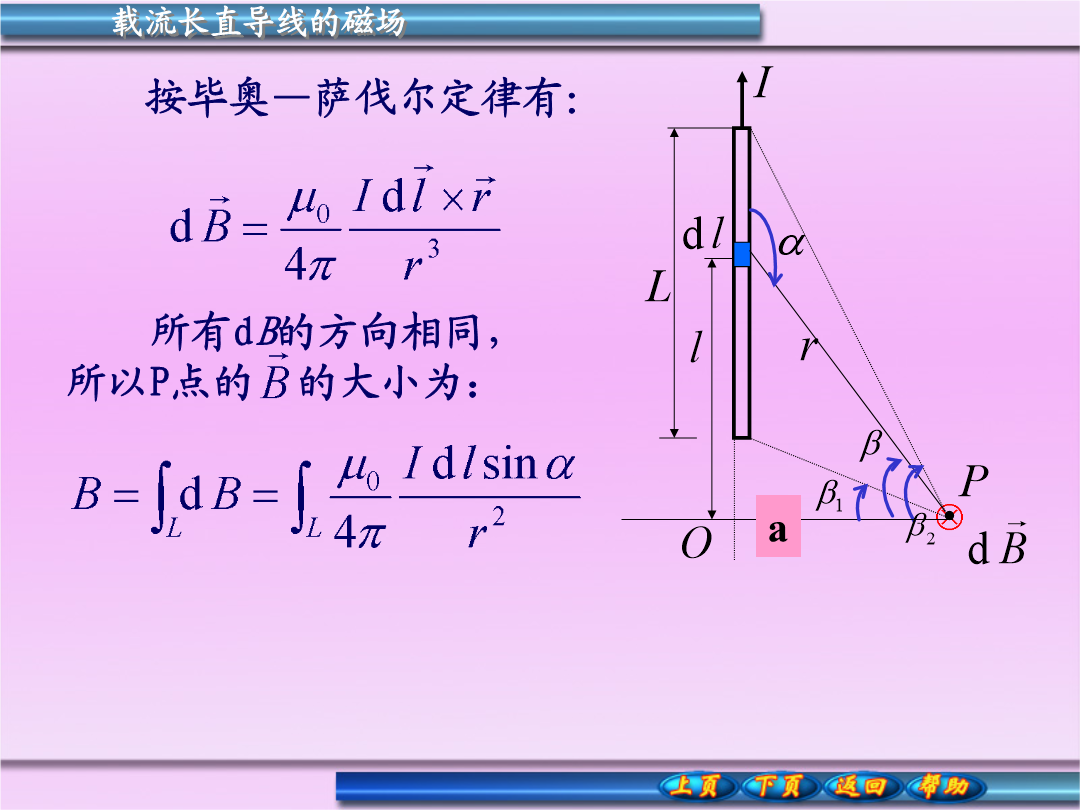
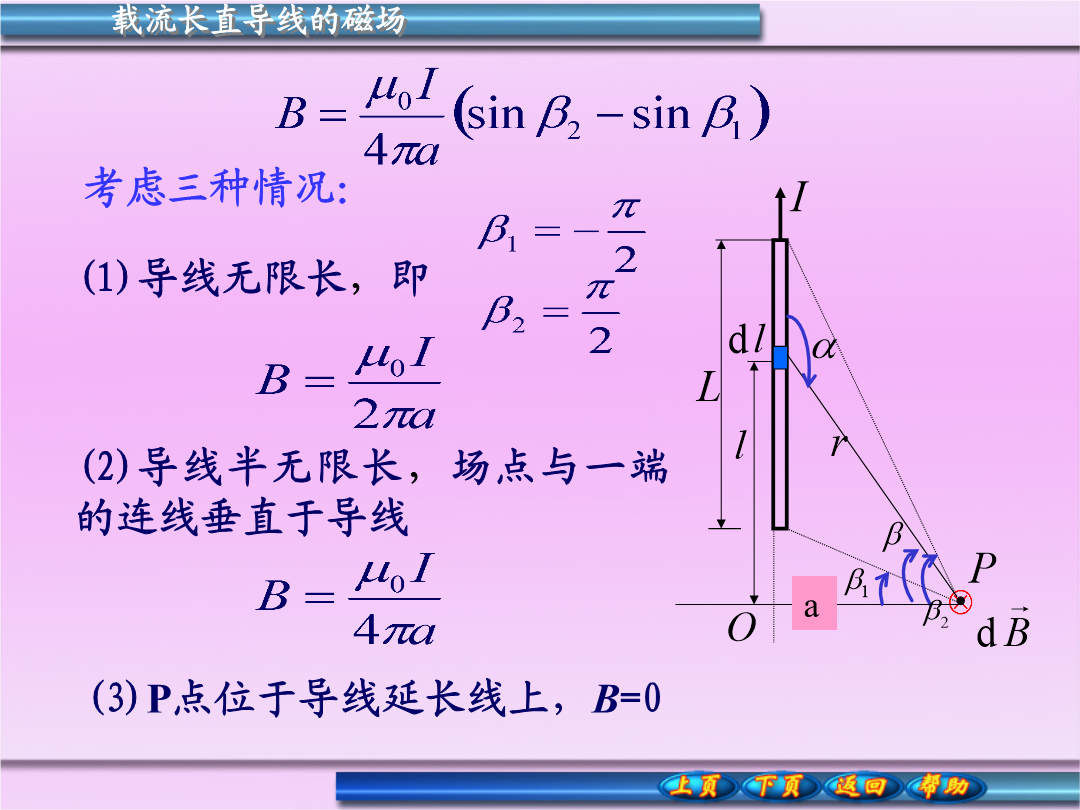
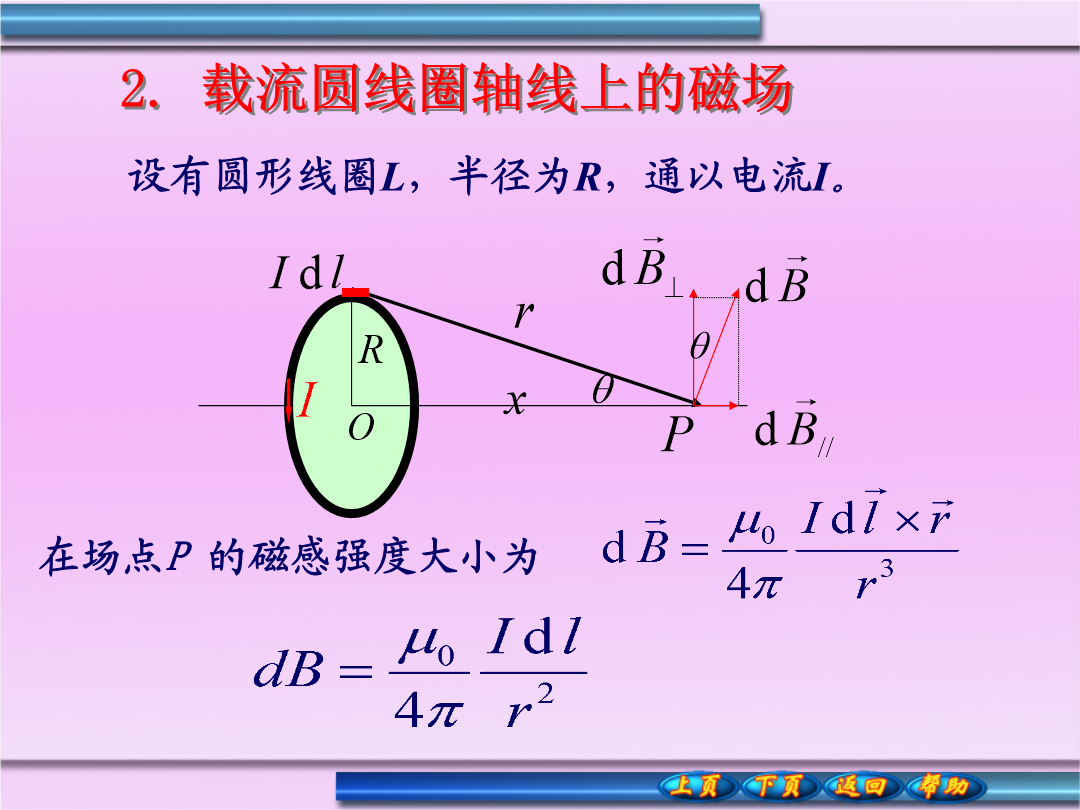
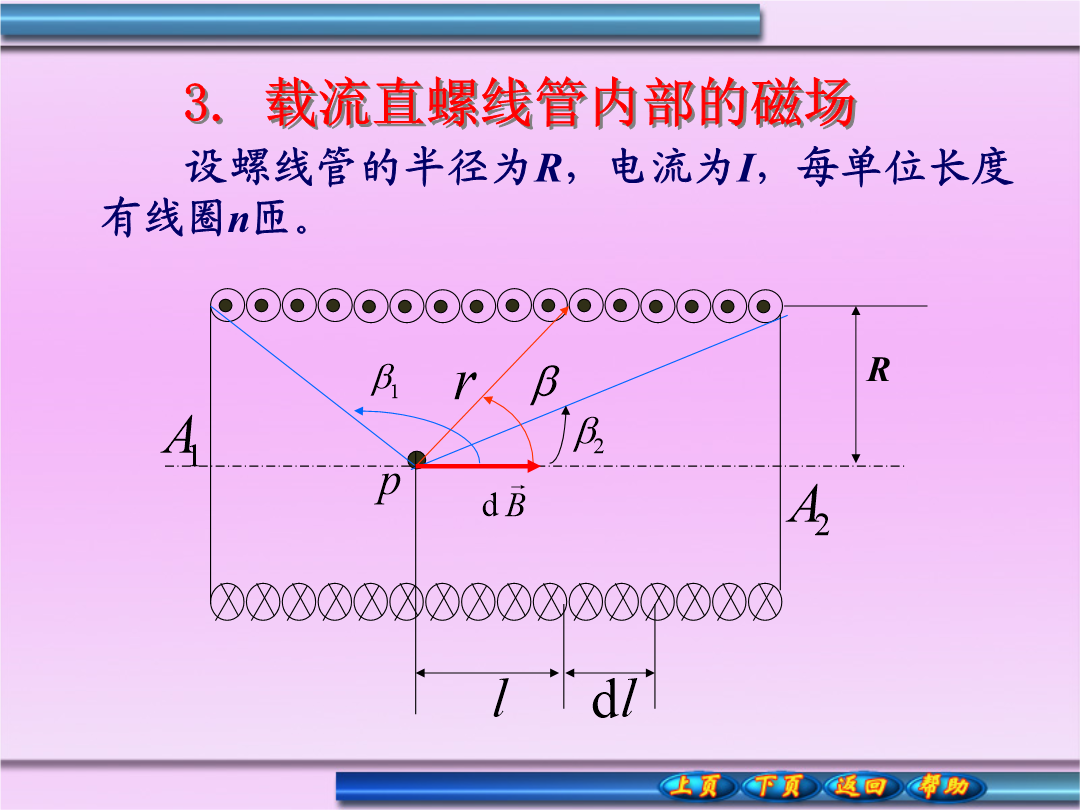
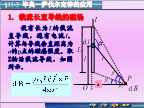
1.载流长直导线的磁场所有dB的方向相同,所以P点的的大小为:由几何关系有:考虑三种情况:2.载流圆线圈轴线上的磁场各电流元的磁场方向不相同,可分解为和,由于圆电流具有对称性,其电流元的逐对抵消,所以P点的大小为:载流圆线圈轴线上的磁场(1)在圆心处3.载流直螺线管内部的磁场由于每匝可作平面线圈处理,ndl匝线圈可作Indl的一个圆电流,在P点产生的磁感应强度:R讨论:例一个半径R为的塑料薄圆盘,电量+q均匀分布其上,圆盘以角速度绕通过盘心并与盘面垂直的轴匀速转动。求圆盘中心处的磁感应强度。例题11-1

载流长直导线的磁场.ppt
1.载流长直导线的磁场所有dB的方向相同,所以P点的的大小为:由几何关系有:考虑三种情况:2.载流圆线圈轴线上的磁场各电流元的磁场方向不相同,可分解为和,由于圆电流具有对称性,其电流元的逐对抵消,所以P点的大小为:载流圆线圈轴线上的磁场(1)在圆心处3.载流直螺线管内部的磁场由于每匝可作平面线圈处理,ndl匝线圈可作Indl的一个圆电流,在P点产生的磁感应强度:R讨论:例一个半径R为的塑料薄圆盘,电量+q均匀分布其上,圆盘以角速度绕通过盘心并与盘面垂直的轴匀速转动。求圆盘中心处的磁感应强度。例题11-1
磁场对载流导线的作用.ppt
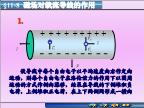
§11-8磁场对载流导线的作用安培定律的微分形式合力作用在长直导线中点,方向沿Z轴正向。例11-6测定磁感应强度常用的实验装置-磁秤如图所示,它的一臂下面挂有一矩形线圈,宽为b,长为l,共有N匝,线圈的下端放在待测的均匀磁场中,其平面与磁感应强度垂直,当线圈中通有电流I时,线圈受到一向上的作用力,使天平失去平衡,调节砝码m使两臂达到平衡。用上述数据求待测磁场的磁感应强度。作用在两侧直边上的力则大小相等,方向相反,它们相互抵消。当天平恢复平衡时,这个向上的安培力恰与调整砝码的重量相等,由此可得如N=9匝,b

磁场对载流导线的作用.pptx
会计学均匀磁场(cíchǎng)中载流直导线所受安培力无限(wúxiàn)长两平行载流直导线间的相互作用力电流(diànliú)单位“安培”的定义解:推论(tuīlùn)②载流线圈在均匀磁场中求载流导线(dǎoxiàn)ab在无限长载流直导线(dǎoxiàn)磁场中的受力(已知:I1、I2、d、L)。求一载流导线框在无限长直导线磁场中的受力和运动(yùndòng)趋势。整个线圈(xiànquān)所受的合力:轨道炮是一种利用电流间相互作用的安培力将弹头(dàntóu)发射出去的武器。两个扁平的互相(hùx
磁场对载流导线的作用.ppt
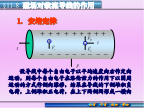
§11-8磁场对载流导线的作用霍耳电场,这电场阻碍自由电子的侧向漂移,当电场力与洛伦兹力平衡时设导线中单位体积的自由电子数为n,它等于导线中单位体积的正离子数。安培定律的微分形式合力作用在长直导线中点,方向沿Z轴正向。例11-6测定磁感应强度常用的实验装置-磁秤如图所示,它的一臂下面挂有一矩形线圈,宽为b,长为l,共有N匝,线圈的下端放在待测的均匀磁场中,其平面与磁感应强度垂直,当线圈中通有电流I时,线圈受到一向上的作用力,使天平失去平衡,调节砝码m使两臂达到平衡。用上述数据求待测磁场的磁感应强度。作用在
