预览加载中，请您耐心等待几秒...

应力及应变状态.pdf

预览
1/10
2/10
3/10
4/10
5/10
6/10
7/10
8/10
9/10
10/10

亲，该文档总共61页，到这已经超出免费预览范围，如果喜欢就直接下载吧～

下载提示 文本预览

如果您无法下载资料，请参考说明：

1、部分资料下载需要金币，请确保您的账户上有足够的金币

2、已购买过的文档，再次下载不重复扣费

3、资料包下载后请先用软件解压，在使用对应软件打开

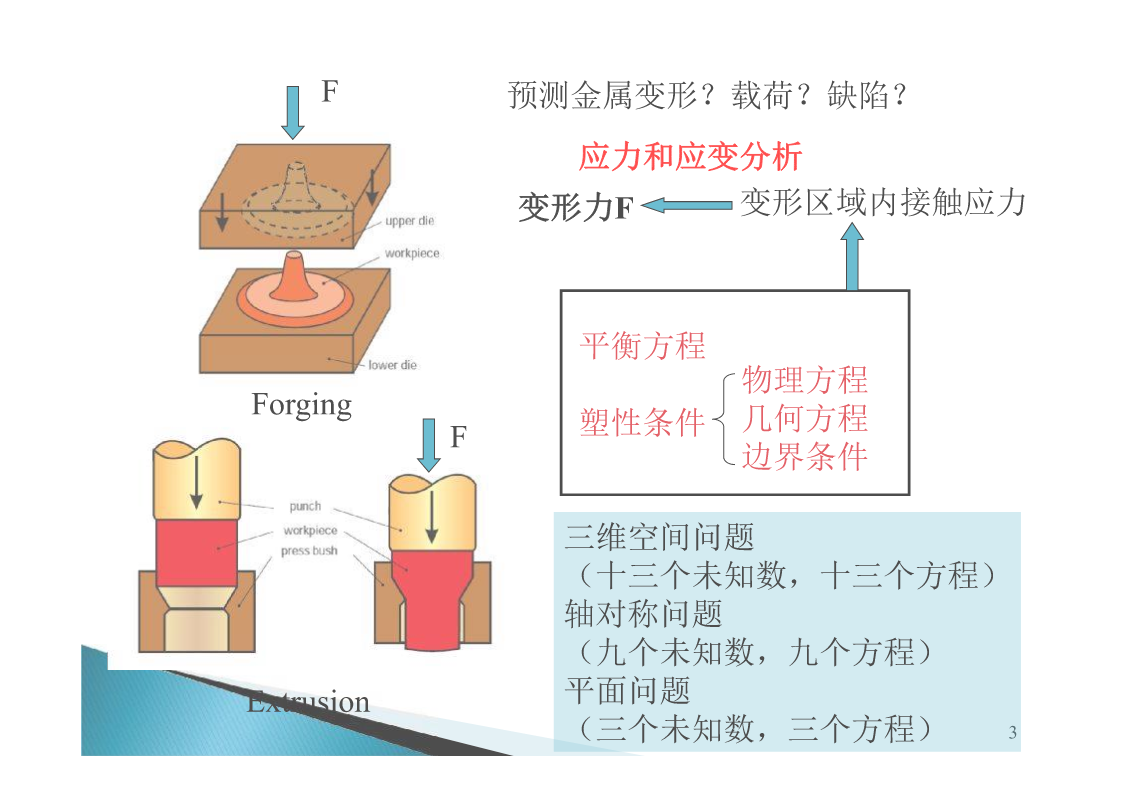
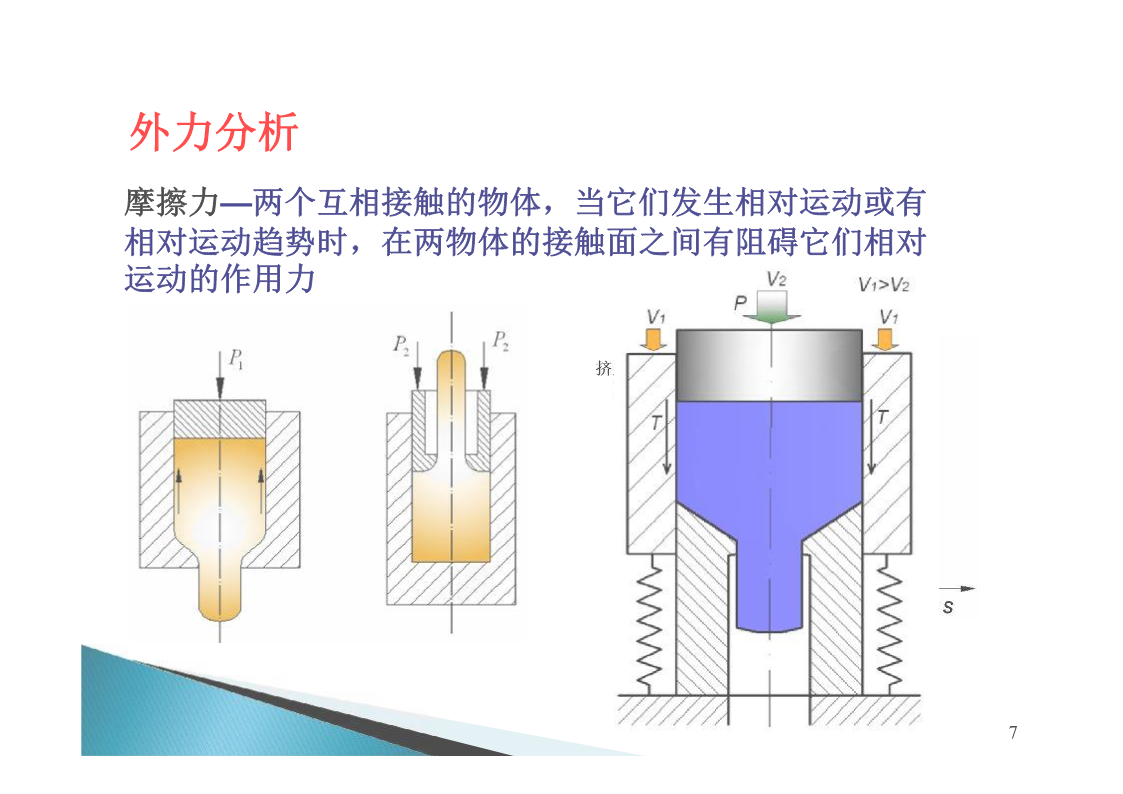
应力状态和应变状态分析 内容 l塑性加工应力分析 —一点附近应力表示方法 l平衡微分方程 l塑性加工应变分析 ---点的应变状态分析 2 F预测金属变形？载荷？缺陷？ 应力和应变分析 变形力F变形区域内接触应力 平衡方程 物理方程 Forging几何方程 F塑性条件 边界条件 三维空间问题 （十三个未知数，十三个方程） 轴对称问题 （九个未知数，九个方程） Extrusion平面问题 （三个未知数，三个方程）3 一、一点附近应力表示法 1.基本概念 外力： 外部施加作用在物体上的力。（接触力，摩擦力，重力等） 内力： 外力作用下，物体各点之间产生相互作用的力。 应力： 变形体中单位面积上的内力。 4 一、一点附近应力表示法 外力分析 正压力—工具与工件接触面上的垂直作用力 5 一、一点附近应力表示法 外力分析 摩擦力—两个互相接触的物体，当它们发生相对运动或有 相对运动趋势时，在两物体的接触面之间有阻碍它们相对 运动的作用力 6 外力分析 摩擦力—两个互相接触的物体，当它们发生相对运动或有 相对运动趋势时，在两物体的接触面之间有阻碍它们相对 运动的作用力 7 Fig.13SpliebynormalforgingFig.14Splinebyoscillatingforging8 90 CCF 80OCF 70 60 50 40 Force(kN) 30 20 10 0246810 Stroke(mm) Fig.12Stroke-forcecurveofOCFcompareditHCCF 9 一、一点附近应力表示法 外力分析 工具形状的影响 T TN N 正压力的水平分量和摩擦力正压力的水平分量和摩擦力 的水平分量方向一致，共同的水平分量方向相反，有利 阻碍金属沿横向流动于金属沿横向流动 10 一、一点附近应力表示法 内力分析 工件中的内力是以应力形式分布的，对工件中内应力分 布规律的分析，主要是为了了解工件爱不同区域内的变 形特征。 11 一、一点附近应力表示法 应力：单位面积上的内力。 在A面上围绕Q点取一很小的面积△A，设 该面积上内力的合力为△F， DFdF S==lim D®F0DAdAst n S为A面上Q点的全应力。它是一个矢量，S 称为应力矢量。 S的方向不一定垂直于微元 面，如果将其分解为垂直于 和平行于微元面的两个分解 内力，则可以得到相应的两 个应力分量，即就是正应力s 和剪应力t作用在变形体中某一微元面积上的应力 12 一、一点附近应力表示法 全应力S是个矢量，可以分解 为两个分量：正应力和切应 力 S2=+st22 微小面积dA可叫做Q点在N 方向的微分面 通过Q点在不同方位的切面 上，全应力S显然是不同的 13 一、一点附近应力表示法 S1，S2，S3……. 如何来确定一点的应力状态？ 可以证明只要知道过该点的 三个相互垂直界面上的三个 应力矢量、则过该点的任意 截面上的应力矢量均可求出， 即就是该点的应力状态可确 定 14 一、一点附近应力表示法 围绕直角坐标系一承受所有S均可求解 任意力系作用物体的任 意点Q切取无限小单元 体，棱边平行于三根坐 标轴。各微分面均有应 力矢量作用，这些矢量 沿坐标轴分解为三个分 量，一是正应力分量， 两个剪应力分量。可见， 一点的应力状态需用九 个应力分量来描述。单元体的受力情况 a）物体内的单元体 b）单元体上的应力状态 15 一、一点附近应力表示法 2.单向应力状态DFdF S==lim D®F0DAdA 应力数值离不开所作用面的方位，应力数值随所作用面 的方位变化而变化。 F 由力的平衡方程F=s0×A0=s1×A1 A1=A0/cosa 因为A1=A0/cosa 所以s1=s0×cosa 外载荷不变的情况下， 应力的数值取决于其所F 作用平面的方位。单向拉伸时轴向应力随截面方位变化 16 一、一点附近应力表示法 3.直角坐标系下一点的应力状态 m ésxtxytxzùx面上 êúl sij=tyxsytyzstyyzn êtyxsytyzúy面上 êú ëtzxtzyszûz面上 方向余弦l,m,n l2+m2+n2=1 x方向y方向z方向 应力分量的正负号规定如下：在单元体上外法 线指向坐标轴正向的微分面叫做正面，反之，称为 负面；对于正面，指向坐标轴正向的应力分量为正，用三个互相垂直面上的 指向负向的为负；对于负面，情况正好相反。应力分量表示一点附近 的应力状态 由可s以找到任意斜面上的正应力s及剪应力 ijNtN 17 一、一点附近应力表示法 3.直角坐标系下一点的应力状态 一点附近应力描述的充分必要条