【数学】332《函数的极值与导数》(新人教B版选修1-1)ppt课件.ppt

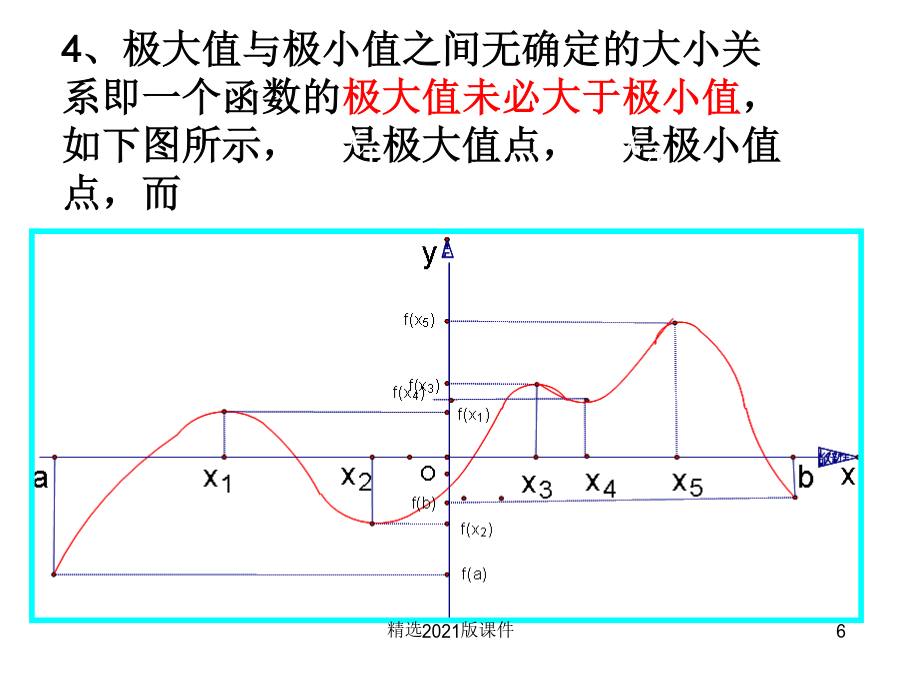
3.3.2函数的极值与导数知识回顾２、用导数法确定函数的单调性时的步骤是：
（1）一般地，设函数y=f(x)在x=x0及其附近有定义，如果f(x0)的值比x0附近所有各点的函数值都大，我们就说f(x0)是函数的一个极大值，记作y极大值=f(x0)，x0是极大值点。如果f(x0)的值比x0附近所有各点的函数值都小，我们就说f(x0)是函数的一个极小值。记作y极小值=f(x0)，x0是极小值点。极大值与极小值统称为极值.1、在定义中，取得极值的点称为极值点，极值点是自变量(x)的值，极值指的是函数值(y)。4、极大值与极小值之间无确定的大小关系即一个函数的极大值未必大于极小值，如下图所示，是极大值点，是极小值点，而二、导数的应用：求函数的极值例１：求f（x）＝x２－x－２的极值.(3)用函数的导数为0的点，顺次将函数的定义区间分成若干小开区间，并列成表格.检查f′(x)在方程根左右的值的符号，求出极大值和极小值.解：例3:下列函数中，x=0是极值点的函数
是()
A.y=－x3B.y=x2
C.y=x2－xD.y=1/x∴a=2.
例6:下列说法正确的是()
A.函数在闭区间上的极大值一定比
极小值大
B.函数在闭区间上的最大值一定是
极大值
C.对于f(x)=x3+px2+2x+1，若|p|＜，
则f(x)无极值
D.函数f(x)在区间(a，b)上一定存在最值15