
多元函数全微分ppt课件.ppt

lj****88




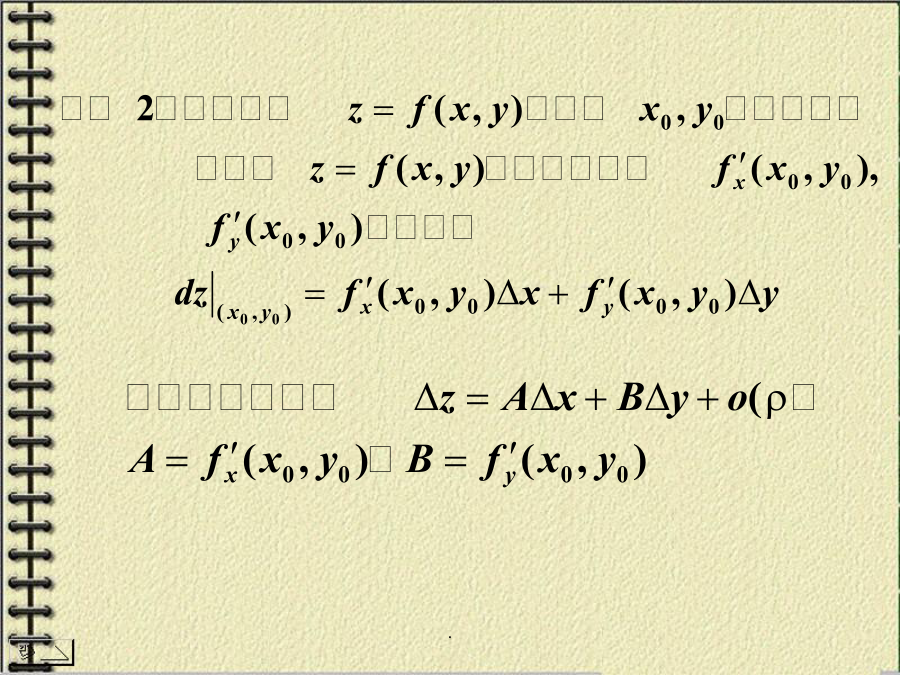
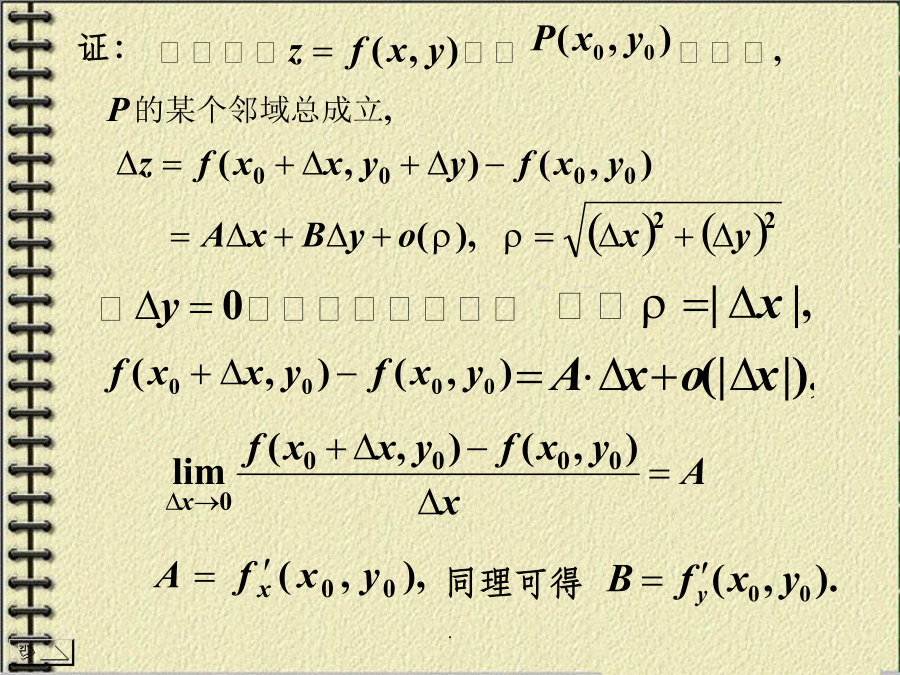


亲,该文档总共33页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

多元函数全微分ppt课件.ppt
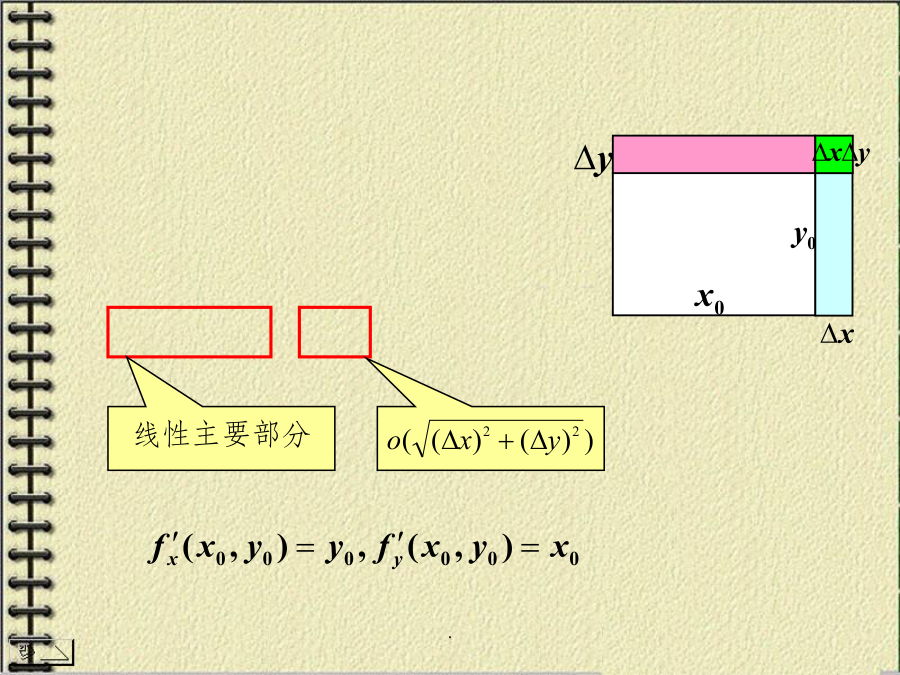
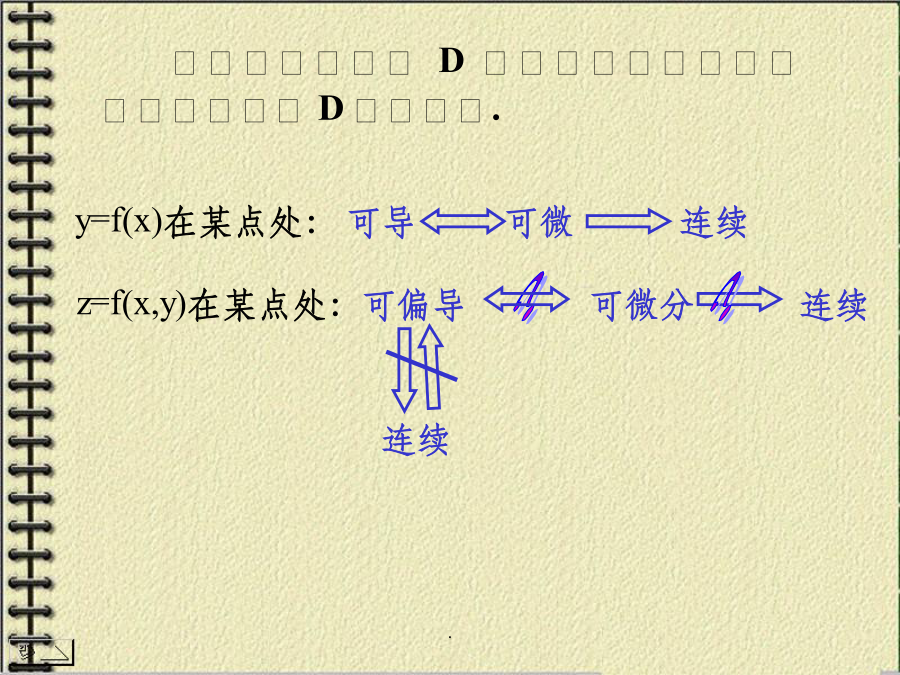
8.3全微分全改变量的概念线性主要部分8.3.1全微分的定义y=f(x)在某点处:可导可微连续证:事实上.证:y=f(x)在某点处:可导可微则说明:多元函数的各偏导数存在并不能保证全微分存在,(依偏导数的连续性)或全微分的定义可推广到三元函数:解解解.证不存在.(4)多元函数连续、可导、可微的关系8.3.3全微分在近似计算中的应用解:设圆柱形容器的半径为r,高为h,例4.解1.多元函数全微分的概念;思考题练习题..练习题答案

多元函数微分ppt课件.ppt
高数课件第八章多元函数微分法及其应用第一节多元函数的基本概念返回第一节多元函数的基本概念一、区域1.邻域设是xOy平面上的一个点,δ是某一正数.与点距离小于δ的点的全体称为的邻域,记为,即也就是2.区域设E是平面上的一个点集,P是平面上的一个点.如果存在点P的某一邻域使,则称P为E的内点(图8-1).如果点集E的点都是内点,则称E为开集.如果点P的任一邻域内既有属P于E的点,也有不属于E的点,E则称P为E的边界点(图8-2).设D是开集.如果对于D内的图8-1任何两点,都可用折线连结起来,而且该折线上的点

34多元函数的偏导数和全微分PPT课件.ppt
一、偏导数的概念在二元函数z=f(x,y)中,有两个自变量x,y,但若固定其中一个自变量,比如,令y=y0,而让x变化.设z=f(X)=f(x,y)在X0=(x0,y0)的某邻域U(X0)内有定义.固定y=y0,在x0给x以增量x.相应函数增量记作则称这个极限值为z=f(x,y)在(x0,y0)处对x的偏导数.称为z=f(x,y)在(x0,y0)处对y的偏导数.称为z对自变量x的偏导函数(简称偏导数)1.由偏导数定义知,所谓f(x,y)对x的偏导数,就是将y看作常数,将f(x,y)看作一元函数来定义的.
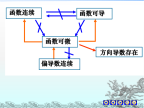
多元函数微分-关系图ppt课件.ppt
1函数在某点连续函数在某点各偏导数都存在,提示:利用而在点(0,0)可微.

多元函数微分-关系图ppt课件.ppt
1函数在某点连续函数在某点各偏导数都存在,提示:利用而在点(0,0)可微.
