
弯曲变形.pptx

lj****88





亲,该文档总共61页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

弯曲变形.pptx
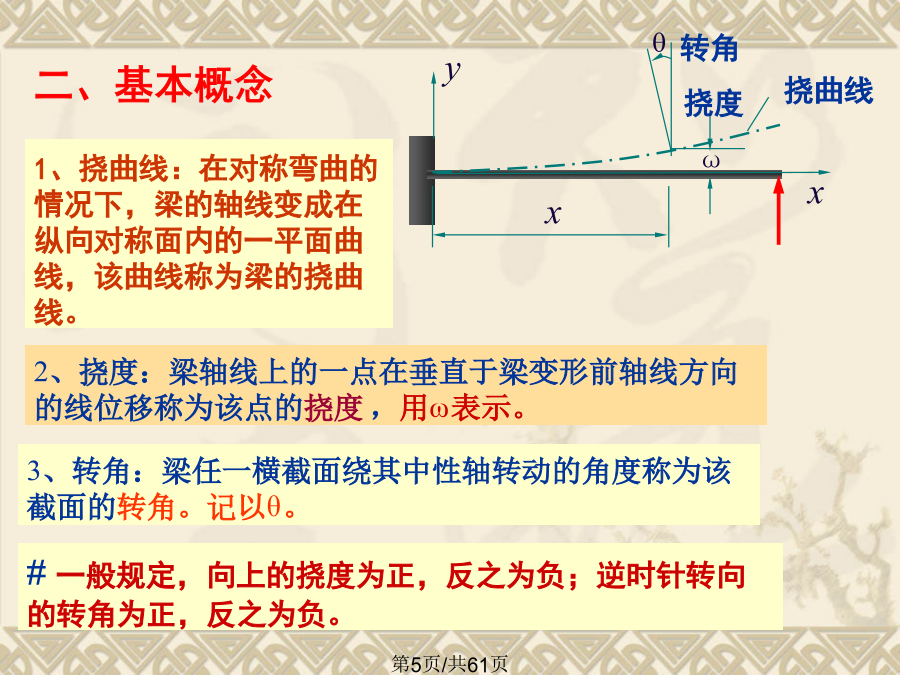
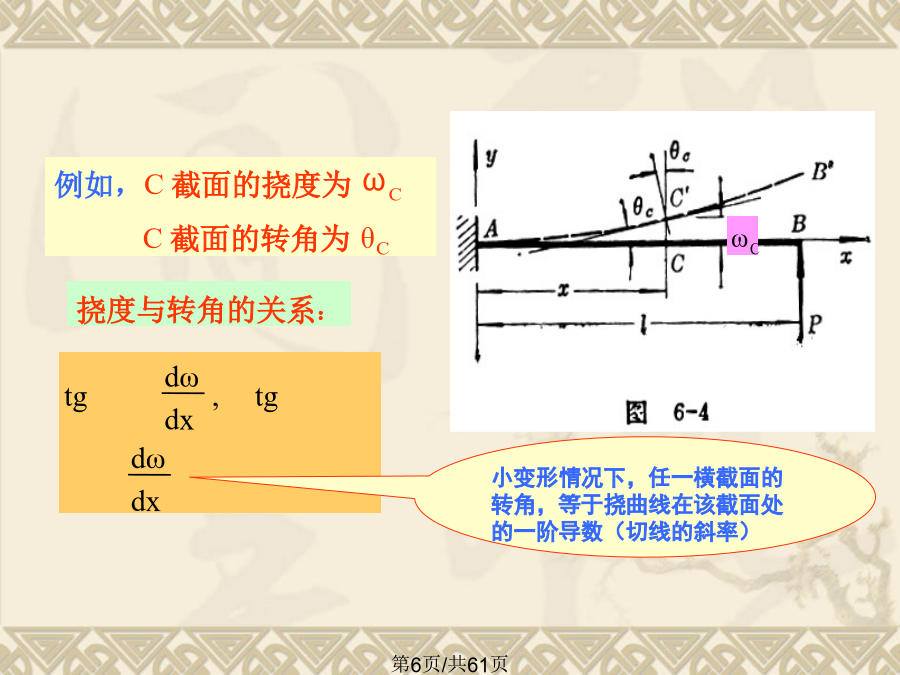
§6.1弯曲变形的概念弯曲变形带来的问题二、基本概念例如,C截面的挠度为ωCC截面的转角为θC假设梁的挠曲线微分方程为由数学知识知:Fs不计§6.3积分法求梁的弯曲变形积分常数C、D由梁的位移边界条件和光滑连续条件确定。2、举例(3)积分将常数C和D代入(c)、(d)得:例6-2一简支梁如图6-9所示,在全梁上受集度为q的均布载荷作用.试求此梁的转角方程和挠度方程,并确定最大转角|θ|max和最大挠度|y|max简支梁的边界条件是:在两支座处的挠度等于零在x=0处,yA=0;在x=l处,yB=0边界条件代

弯曲变形_.ppt
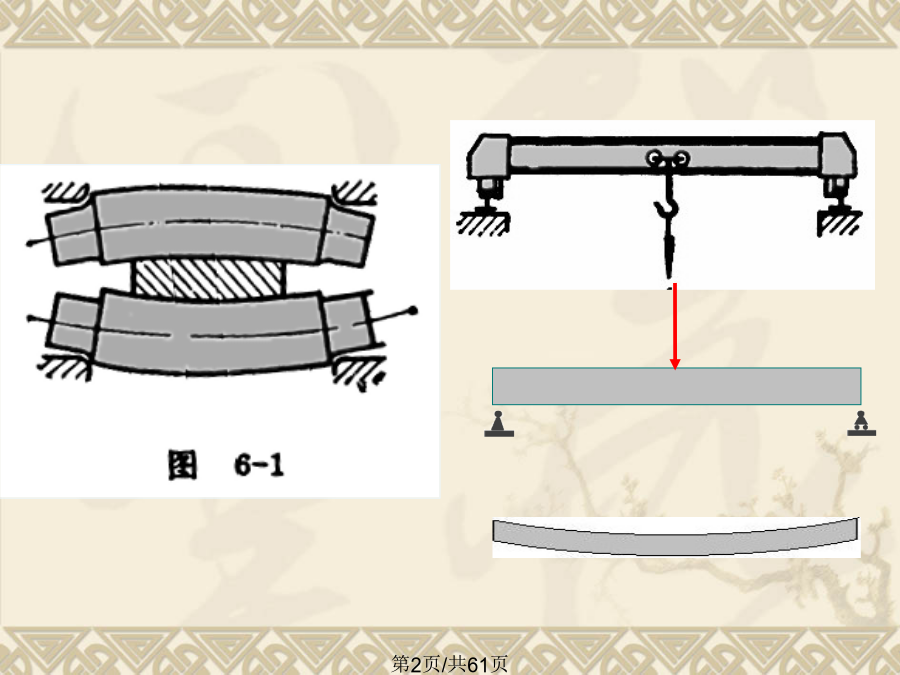
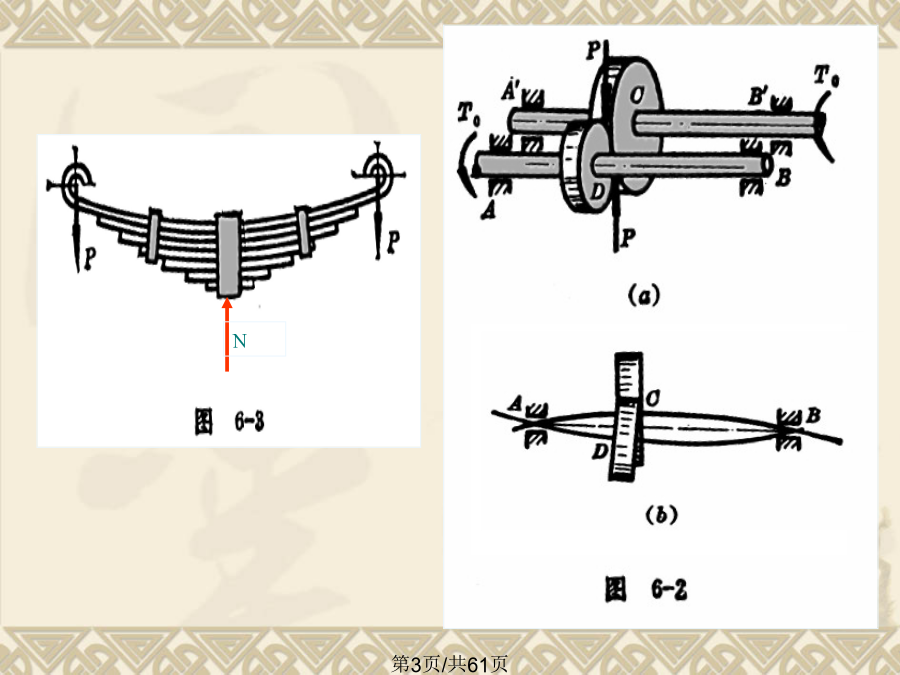
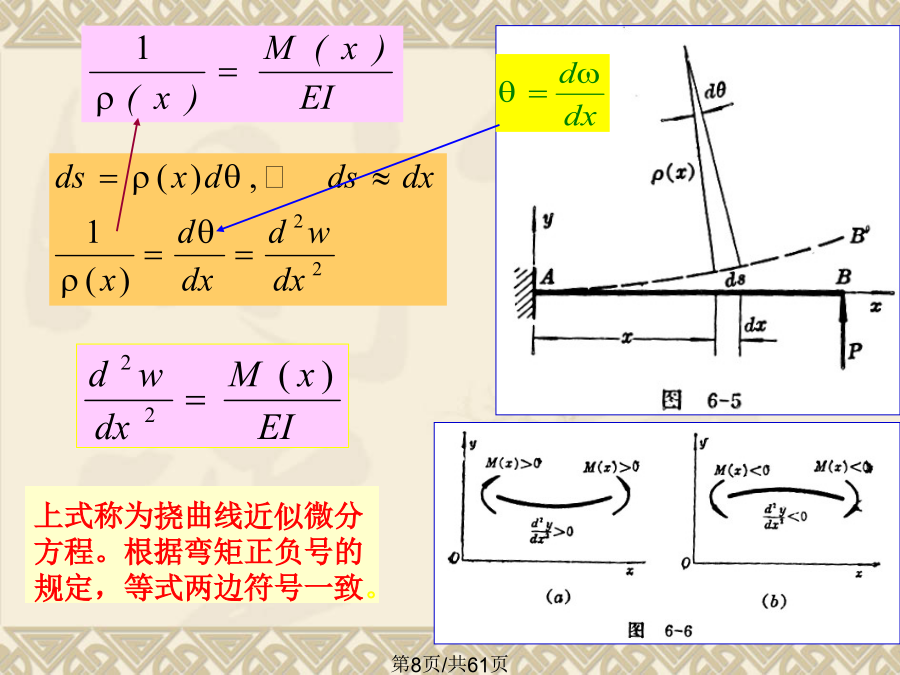
第六章弯曲变形本章内容弯曲变形/工程中的弯曲变形问题弯曲变形/工程中的弯曲变形问题弯曲变形/工程中的弯曲变形问题弯曲变形/工程中的弯曲变形问题弯曲变形/工程中的弯曲变形问题§6.2挠曲线的微分方程弯曲变形/挠曲线的微分方程挠曲线上横坐标为x的任意点的纵坐标。即:截面形心沿y方向的位移,以w表示。w与坐标轴同向为正。横截面相对于原来位置转过的角度,以表示。亦等于x轴与挠曲线切线的夹角。弯曲变形/挠曲线的微分方程推导公式2.由数学得到平面曲线的曲率在规定的坐标系中,x轴水平向右为正,w轴竖直向上为正.此式

弯曲变形浏览.pptx
§6-1工程中的弯曲变形问题§6-2挠曲线的微分方程§6-3积分法求弯曲变形§6-4用叠加法求弯曲变形§6-5简单超静定梁§6-6提高弯曲刚度的一些措施§6-7梁的刚度校核§6–1工程中的弯曲变形问题过大的弯曲变形的危害1.挠度:横截面形心沿垂直于轴线方向的线位移。用v表示。与f同向为正,反之为负。二、挠曲线近似微分方程对于等截面直梁,挠曲线近似微分方程可写成如下形式:支点位移条件:梁的边界条件及内力特征例1求自由端受集中力作用的等截面直梁的弹性曲线方程、最大挠度及最大转角。写出弹性曲线方程并画出曲线

十二 弯曲变形.ppt
第十二章弯曲变形摇臂钻床的摇臂或车床的主轴变形过大,就会影响零件的加工精度,甚至会出现废品。桥式起重机的横梁变形过大,则会使小车行走困难,出现爬坡现象。但在另外一些情况下,有时却要求构件具有较大的弹性变形,以满足特定的工作需要。二、计算弯曲变形的目的三、弯曲变形的基本概念2.挠度和转角四、画绕曲线近似形状的方法2、考虑弯矩的变化例:§12.2挠曲线近似微分方程及其积分——挠曲线的近似微分方程二、积分法求弯曲变形固定端:w=0,θ=0例:已知梁的抗弯刚度为EI。试求图示简支梁在均布载荷q作用下的转角方程、挠

弯曲变形正式.pptx
弯曲变形正式234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253工程中,[w]常用梁的计算跨度l的若干分之一表示,例如:5556575859606162636465666768697071727374757677
