
误差理论与数据处理绪论ppt课件.ppt

ca****ng








亲,该文档总共86页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

误差理论与数据处理绪论ppt课件.ppt
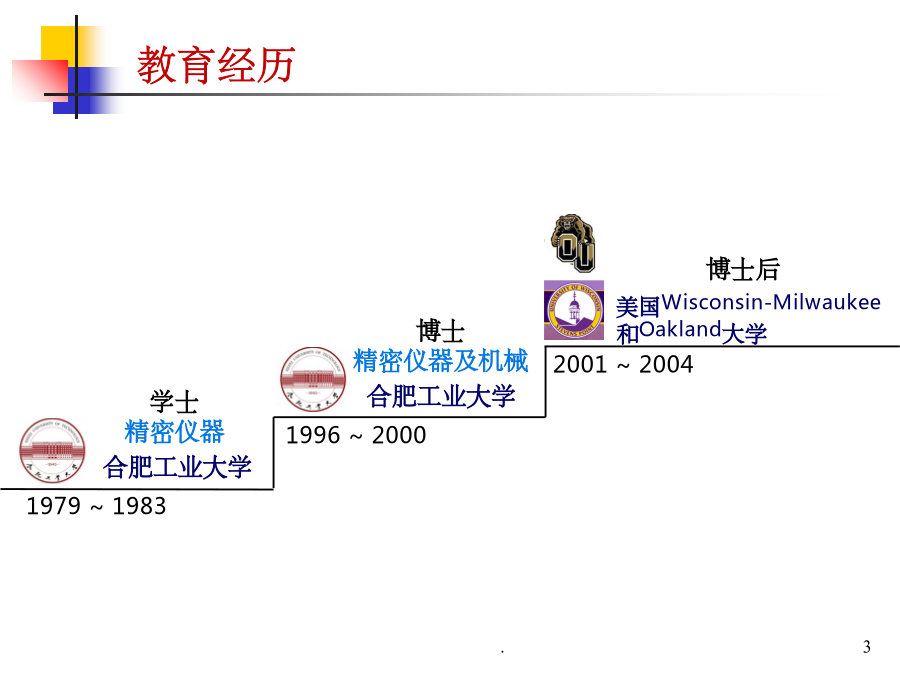
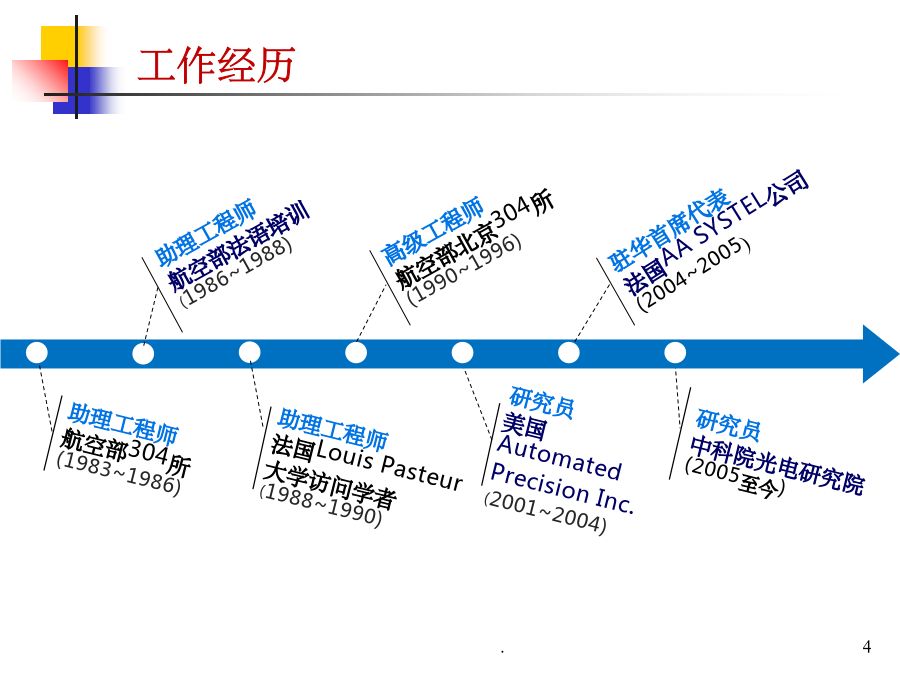
误差理论与数据处理周维虎,1962年7月生,合肥工业大学精密仪器及机械专业博士。中国科学院光电研究院研究员,中国科学院大学博士生导师。从事精密仪器与计量测试研究30余年,主持完成国家级科研项目20余项,获得省部级科技奖励5项,申请发明专利20余项,发表论文90余篇,编写教材1部,起草国家计量检定规程和规范4部。1979~1983国家发明奖和科技进步奖评审专家中国机械工业科学技术奖评审专家科技部先进制造领域十三五重大科技任务实施方案编写组专家科技部重大科学仪器设备开发十三五重大科技任务实施方案编写组专家国防
误差理论与数据处理-绪论实用全套PPT.ppt
绪论教学(jiāoxué)目的和要求主要(zhǔyào)内容重点(zhòngdiǎn)和难点教学(jiāoxué)目的和要求误差公理:测量结果都具有误差,误差自始至终存在于一切(yīqiè)科学实验和测量的过程之中。被测量者的血压值不仅受患者疾病因素的影响,同时还受被测量者的情绪、运动程度、测量时间等外界因素的影响,使被测量者的自身(zìshēn)血压也在变化。主要(zhǔyào)内容研究(yánjiū)误差的意义重点(zhòngdiǎn)和难点重点(zhòngdiǎn)和难点误差具有普遍性和必然性。·温

误差理论与数据处理(绪论).ppt
误差理论与数据处理周维虎,1962年7月生,合肥工业大学精密仪器及机械专业博士。中国科学院光电研究院研究员,中国科学院大学博士生导师。从事精密仪器与计量测试研究30余年,主持完成国家级科研项目20余项,获得省部级科技奖励5项,申请发明专利20余项,发表论文90余篇,编写教材1部,起草国家计量检定规程和规范4部。1979~1983国家发明奖和科技进步奖评审专家中国机械工业科学技术奖评审专家科技部先进制造领域十三五重大科技任务实施方案编写组专家科技部重大科学仪器设备开发十三五重大科技任务实施方案编写组专家国防

误差理论与数据处理绪论.pptx
误差理论与数据处理绪论《误差理论与数据处理》《误差理论与数据处理》《误差理论与数据处理》《误差理论与数据处理》《误差理论与数据处理》《误差理论与数据处理》《误差理论与数据处理》《误差理论与数据处理》《误差理论与数据处理》《误差理论与数据处理》《误差理论与数据处理》《误差理论与数据处理》《误差理论与数据处理》《误差理论与数据处理》《误差理论与数据处理》《误差理论与数据处理》《误差理论与数据处理》《误差理论与数据处理》《误差理论与数据处理》《误差理论与数据处理》《误差理论与数据处理》《误差理论与数据处理》《误

误差理论与数据处理(绪论).ppt
误差理论与数据处理周维虎,1962年7月生,合肥工业大学精密仪器及机械专业博士。中国科学院光电研究院研究员,中国科学院大学博士生导师。从事精密仪器与计量测试研究30余年,主持完成国家级科研项目20余项,获得省部级科技奖励5项,申请发明专利20余项,发表论文90余篇,编写教材1部,起草国家计量检定规程和规范4部。1979~1983国家发明奖和科技进步奖评审专家中国机械工业科学技术奖评审专家科技部先进制造领域十三五重大科技任务实施方案编写组专家科技部重大科学仪器设备开发十三五重大科技任务实施方案编写组专家国防
