
函数单调性与导数ppt课件.ppt

ca****ng








亲,该文档总共18页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

函数的单调性与导数ppt课件.ppt
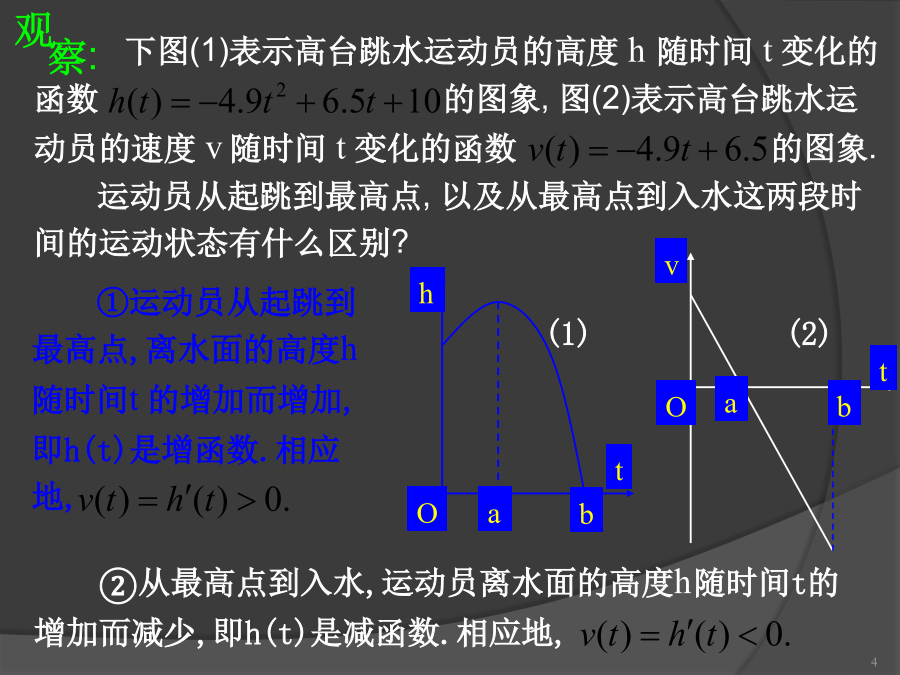
1.3.1函数的单调性与导数温故知新问题1:导数的几何意义?x1思考:那么判断下列函数的单调性?高台跳水运动员的高度h随时间t变化的函数h(t)=-4.9t2+6.5t+10再观察下面一些函数的图象,探讨导函数的正负与其对应函数的单调性的关系:导数f(x0)表示函数f(x)在点(x0,f(x0))处的切线的斜率例1.已知导函数f(x)的下列信息:解:(3)f(x)=____________例2.判断下列函数的单调性,并求出单调区间:④解不等式f(x)<0,解集在定义域内的部分为减区间;练习例3.如

函数单调性与导数ppt课件.ppt
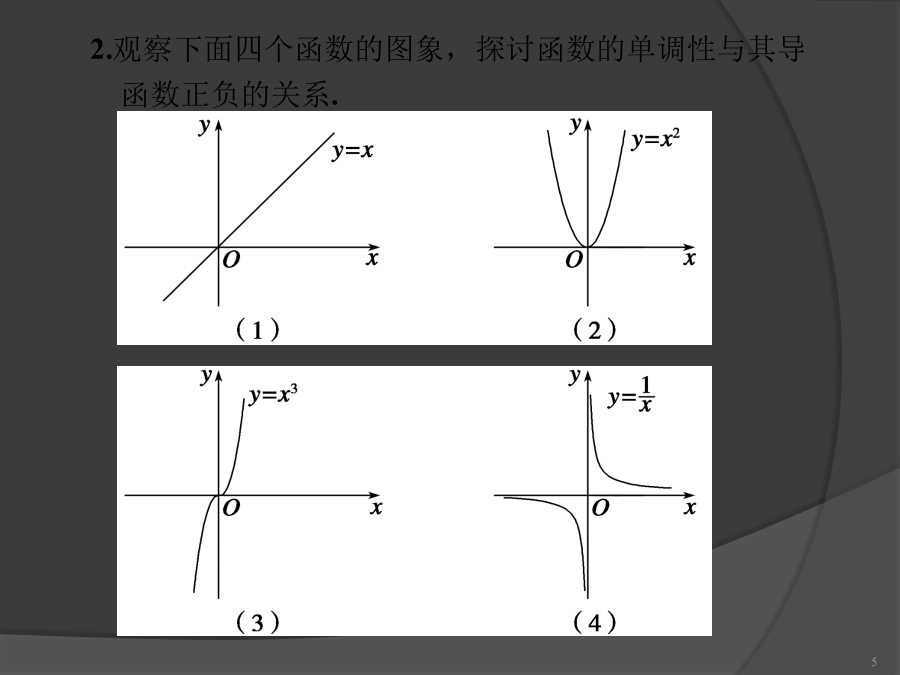
导数在研究函数中的应用函数y=f(x)在给定区间G上,当x1、x2∈G且x1<x2时2:常见函数的导数:观察:5设函数y=f(x)在某个区间(a,b)内有导数,如果在这个区间内f′(x)>0,那么y=f(x)为这个区间内的增函数;如果在这个区间内f′(x)<0,那么y=f(x)为这个区间内的减函数.新知2:如果在某个区间内恒有f´(x)=0,则f(x)为函数f′(x)>0是f(x)为增函数的条件;f′(x)≥0是f(x)为增函数的条件.即若在某个区间上有有限个点使得f'(x)=0,而在其余的点恒有f'(x

函数的单调性与导数ppt课件.ppt
函数的单调性与导数1.理解函数单调性和导数的关系;2.会利用导数判断函数的单调性。学习重点和难点1.重点:函数单调性和导数的关系2.难点:函数单调性和导数的关系。知识回顾图象是单调上升的.图象是单调下降的.图象是单调上升的.图象是单调下降的.函数的单调性与其导函数正负的关系:单调性函数单调性与导数正负的关系1.应用导数求函数的单调区间求函数的单调区间。例2、已知导函数的下列信息:当1<x<4时,当x>4,或x<1时,当x=4,或x=1时,试画出函数f(x)图象的大致形状。4例3、判断下列函数的单调性,并求

函数的单调性与导数的关系ppt课件.ppt
通过观察图像,我们可以发现:(1)运动员从起跳到最高点,离水面的高度h随时间t的增加而增加,即是增函数。相应地,(2)从最高点到入水,运动员离水面的高度h随时间t的增加而减小,即是减函数。相应地,一般地,函数的单调性与其导函数的正负有如下关系:在某个区间(a,b)内,如果,那么函数在这个区间内单调递增;如果,那么函数在这个区间内单调递减。例1:判断下列函数的单调性,并求出单调区间:5点评:1、方法:定义法和导数法,优先选择导数法。例2:已知导函数的下列信息:解:小结:谢谢大家,请多指教.

1函数的单调性与导数ppt课件.ppt
1.3.1函数的单调性与导数(4).对数函数的导数:复习:导数的运算法则:一、复习回顾复合函数的导数:函数y=f(x)在给定区间G上,当x1、x2∈G且x1<x2时o(1)函数的单调性也叫函数的增减性;2x动态演示函数单调性与导数正负的关系例1已知导函数的下列信息:已知导函数的下列信息:已知导函数的下列信息:x例2判断下列函数的单调性,并求出单调区间:例2判断下列函数的单调性,并求出单调区间:总结:当遇到三次或三次以上的,或图象很难画出的函数求单调性问题时,应考虑导数法。3。证明可导函数f(x)在(a,b
