抽样与抽样分布(5).ppt

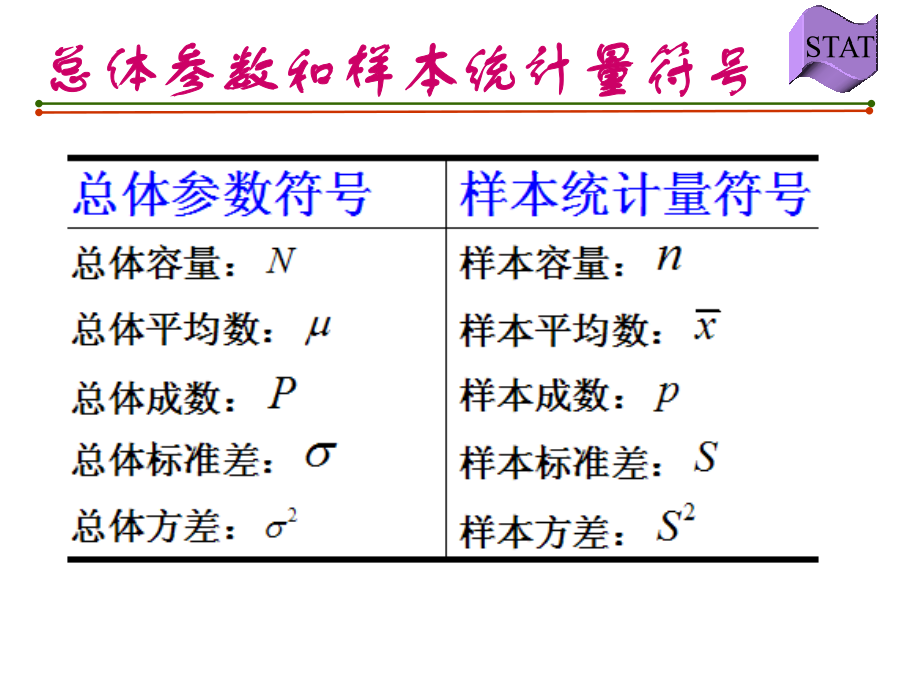
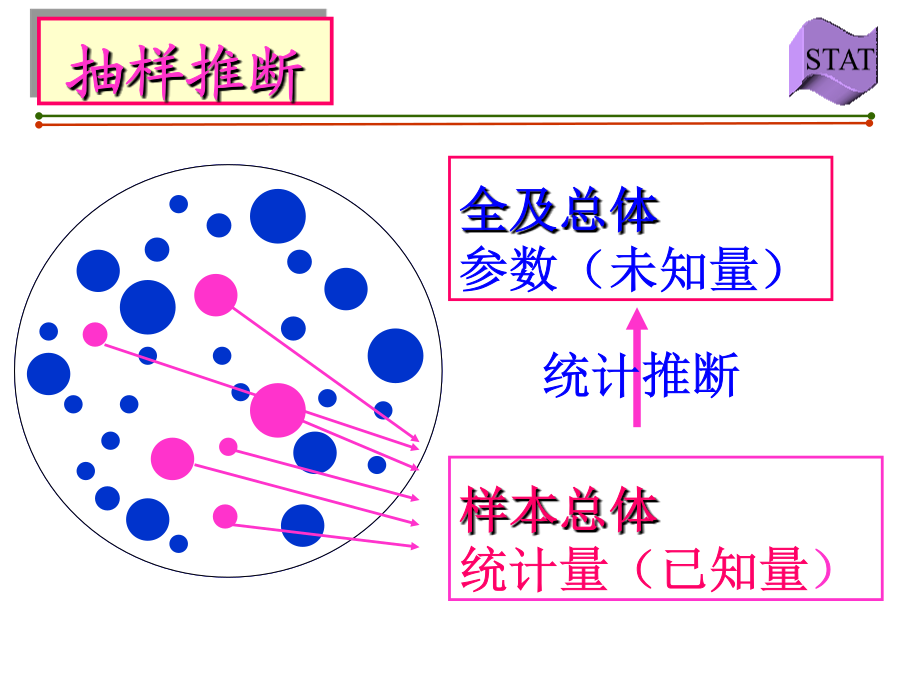
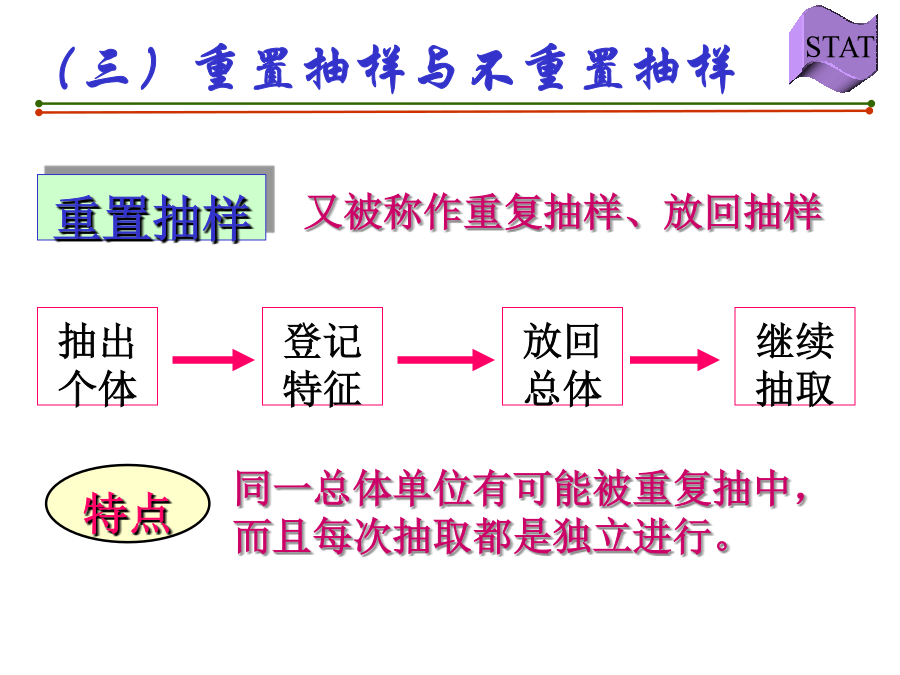
第一节抽样及抽样组织形式
第二节常见的概率分布
第三节抽样分布第5章抽样和抽样分布指样本单位的抽取不受主观因素及其他系统性因素的影响，每个总体单位都有均等的被抽中机会不可能进行全面调查时
不必要进行全面调查时
来不及进行全面调查时
对全面调查资料进行补充修正时第一节抽样及抽样组织形式一、抽样的几个基本概念（二）总体参数和样本统计量总体参数和样本统计量符号（三）重置抽样与不重置抽样（三）重置抽样与不重置抽样二、抽样组织形式随机原则的实现随机数字表二、抽样组织形式二、抽样组织形式二、抽样组织形式二、抽样组织形式第二节常见的概率分布一、正态分布正态分布的特征和对正态曲线的影响正态分布的概率（二）标准正态分布（二）标准正态分布（三）正态分布的概率计算【例】设X~N(0，1)，求以下概率：
(1)P(X<1.5)；(2)P(X>2)；(3)P(-1<X3)；(4)P(|X|2)
解：(1)P(X<1.5)=(1.5)=0.9332
(2)P(X>2)=1-P(2X)=1-0.9973=0.0227
(3)P(-1<X3)=P(X3)-P(X<-1)
=(3)-(-1)=(3)–[1-(1)]
=0.9987-(1-0.8413)=0.8354
(4)P(|X|2)=P(-2X|2)=(2)-(-2)
=(2)-[1-(2)]=2(2)-1=0.9545【例】设X~N(5，32)，求以下概率
(1)P(X10)；(2)P(2<X<10)
解：(1)二、二项分布三、t分布具有自由度为n的t分布的随机变量T的数学期望和方差为:
E(T)=0;D(T)=n/(n-2),对n>2不难看到，当n充分大时，t分布近似N(0,1)分布.但对于较小的n，t分布与N(0,1)分布相差很大.四、卡方分布2分布的特点c2分布
应用中心极限定理可得，若由统计学家费舍(R.A.Fisher)提出的，以其姓氏的第一个字母来命名则
设若U为服从自由度为n1的2分布，即U~2(n1)，V为服从自由度为n2的2分布，即V~2(n2),且U和V相互独立，则

称F为服从自由度n1和n2的F分布，记为F分布即它的数学期望并不依赖于第一自由度n1.第三节抽样分布一、抽样推断的理论基础【例】设一个总体，含有4个元素（个体），即总体单位数N=4。4个个体分别为X1=1、X2=2、X3=3、X4=4。总体的均值、方差及分布如下现从总体中抽取n＝2的简单随机样本，在重复抽样条件下，共有42=16个样本。所有样本的结果如下表计算出各样本的均值，如下表。并给出样本均值的抽样分布所有样本均值的均值和方差样本均值的分布与总体分布的比较中心极限定理中心极限定理二、单一总体样本均值、样本比例的抽样分布样本均值的数学期望

样本均值的方差
重复抽样

不重复抽样样本比例的数学期望

样本比例的方差
重复抽样

不重复抽样例3：假定某统计人员在填写的报表中有2%至少会
有一处错误，如果我们检查了一个有600份报表组
成的随机样本，其中至少有一处错误的报表所组
成的比例在0.025~0.070之间的概率有多大？三、两个总体均值之差、比例之差的抽样分布两个总体都为正态分布，即

两个样本均值之差的抽样分布服从正态分布，其分布的数学期望为两个总体均值之差
方差为各自的方差之和 两个总体均值之差的抽样分布例1。设有甲、乙两所著名高校在某年新生录取时，甲
校的平均分为655分，且服从正态分布，标准差为20分，
乙校的平均分为625分，也服从正态分布，标准差为25
分。现从甲、乙两校随机抽取8名新生计算其平均分，
出现甲校比乙校的平均分低的可能性有多大？分别从两个总体中抽取容量为n1和n2的独立样本，当两个样本都为大样本时，两个样本比例之差的抽样分布可用正态分布来近似
分布的数学期望为

方差为各自的方差之和