
反例函数中k的几何意义及其应用.docx

快乐****蜜蜂



在线预览结束,喜欢就下载吧,查找使用更方便
相关资料

反例函数中k的几何意义及其应用.docx
反例函数中k的几何意义及其应用题目:反例函数中k的几何意义及其应用摘要:反例函数在数学领域中起着重要的作用。其中,k是一个参数,它在反例函数中具有重要的几何意义。本文将从几何的角度探讨k的意义,并介绍反例函数中k的应用。首先,我们将解释k的几何解释,然后讨论它在拓扑学、代数学和几何学中的应用。引言反例函数是一种用于举例证明某种命题不正确的函数。通常情况下,这些函数涉及到一些参数,其中之一就是k。该参数在反例函数中通常具有重要的几何意义。不同的值k可以给出不同的例子,帮助我们理解数学中的一些概念和定理。本文

反比例函数中k的几何意义及应用.doc
反比例函数中k的几何意义及应用【完整版】(文档可以直接使用,也可根据实际需要修订后使用,可编辑放心下载)例析反比例函数中k的几何意义及应用陆智勇OBP(m,n)xoAyAP(m,n)图①xy反比例函数中k的几何意义就是反比例函数图象上的任意一点的横坐标与纵坐标的乘积都等于比例系数K的值,如图①所示.过P作x轴、y轴的垂线PA、PB,垂足为A、B,连结OP,那么有〔1〕=PA·PB=|y|·|x|=|xy|=|k|;〔2〕.能灵活运用这两个结论解有关反比例函数的问题,会给解题带来很多方便。现略举说明。求交点
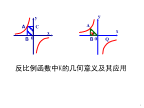
反比例函数中K的几何意义及其应用复习课(课堂PPT).ppt
Q1、如图所示,四边形是矩形,反比例函数过点A,则S矩形ABOC=;2、若连接AO,则=;Q1、如图,若反比例函数的图象过点A,矩形ABOC的面积为4,则k=.2、如图,过反比例函数y=(x>0)图象上一点A作AM⊥x轴于点M,连接OA,则变式训练13.在双曲线上任取一点P,过点P分别作x轴、y轴的垂线段,与x轴y轴所围成的矩形面积为12,则该双曲线的解析式为.【例1】如图,双曲线经过Rt△BOC斜边上的点A,且满足,与BC交于点D,S△BOD=21,则K的值为________。(2015深圳中考15题)

53反比例函数中k的几何意义及应用.doc
反比例函数应用学案(3)学习内容:反比例函数中k的几何意义及应用龙三中夏祥莉研究函数问题要透视函数的本质特征。反比例函数中,比例系数k有一个很重要的几何意义,那就是:过反比例函数图象上任一点P作x轴、y轴的垂线PM、PN,垂足为M、N(如图1所示),则矩形PMON的面积S=PM·PN=|y|·|x|=|xy|=|k|。所以,对双曲线上任意一点作x轴、y轴的垂线,它们与x轴、y轴所围成的矩形面积为常数。从而有。在解有关反比例函数的问题时,若能灵活运用反比例函数中k的几何意义,会给解题带来很多方便。现举例说明

反比例函数中k值几何意义的应用.docx
反比例函数中k值几何意义的应用反比例函数是一种常见的数学函数类型,其中,两个变量的乘积等于一个常数。在反比例函数中,k值代表着两个变量之间的关系强度以及其几何意义,它在许多实际问题的解决中具有广泛的应用。本文将深入探讨反比例函数中k值的几何意义及其应用。一、反比例函数的定义和基本特点反比例函数的标准定义为:当x和y(y≠0)满足xy=k时,我们称y与x成反比例关系,并表示为y=k/x。其中,k是一个常数,称为比例常数。反比例函数的图像是一个曲线,通常被称为双曲线。具体形状取决于k值的正负和绝对值大小。当k
