
方波信号ft展开为傅里叶级数ppt课件.ppt

天马****23



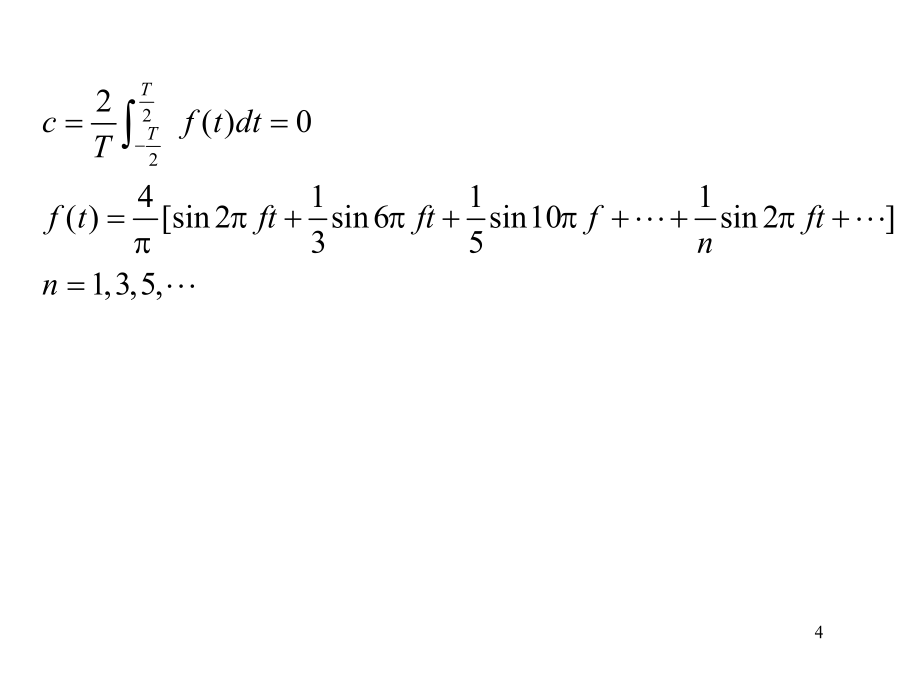

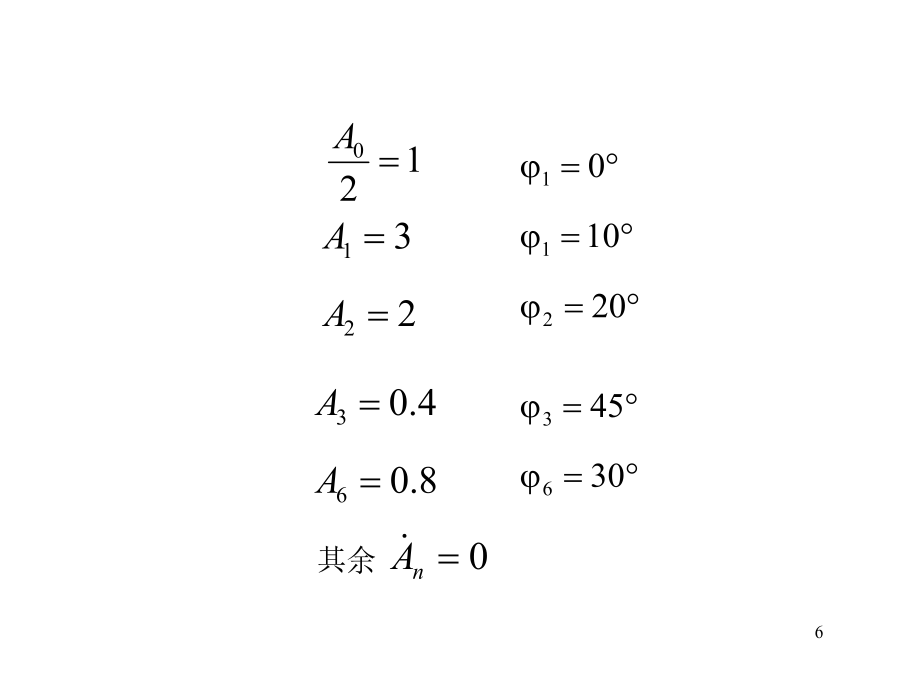



亲,该文档总共84页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

方波信号ft展开为傅里叶级数ppt课件.ppt
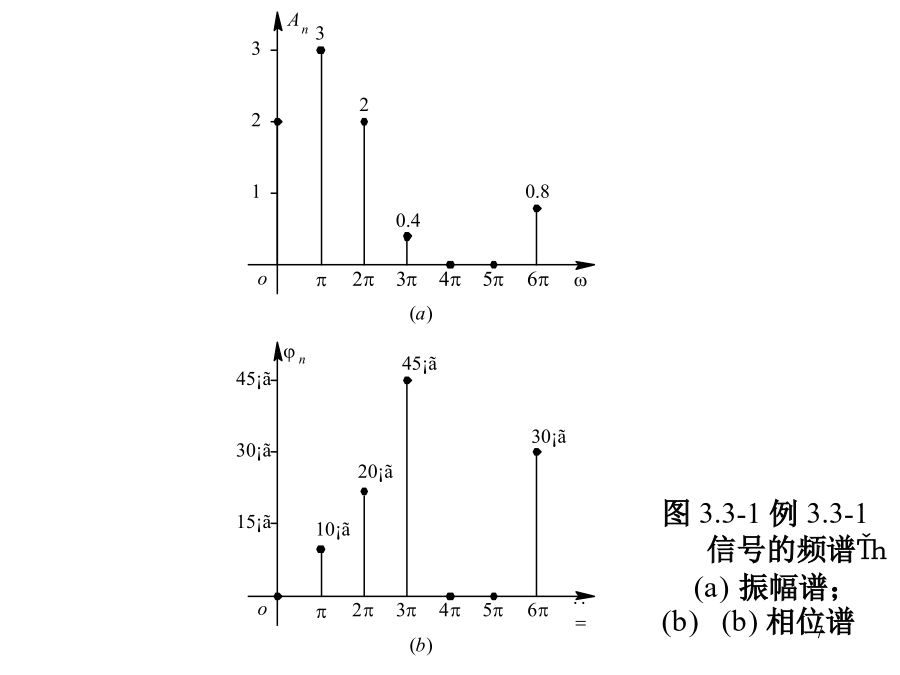
图4.2方波信号的傅里叶级数解我们将信号按式(4―6)分解成傅里叶级数,并按式(4―7)、(4―8)、(4―9)分别计算an,bn及c。34例3.3-1其余图3.3-1例3.3-1信号的频谱振幅谱;(b)相位谱图3.3-2例3.3-1信号的双边频谱(a)振幅谱;(b)相位谱例3.4-2求指数函数f(t)的频谱函数。其振幅频谱及相位频谱分别为(4―41)图4.7单边指数信号及其频谱例3.4-3求图3.4-3(a)所示双边指数函数的频谱函数。图3.4-3双边指数函数及其频谱(a)双边指数函数;(b)频谱

方波信号展开为傅里叶级数.doc
【例4.2-1】将下图所示方波信号展开为傅里叶级数。……0……t解:按题意方波信号在一个周期内的解析式为分别求得傅里叶系数:即:故得信号的傅里叶级数展开式为它只含有一、三、五、……等奇次谐波分量。【例4.2-2】将下图所示信号展开为傅里叶级数。2……0……t-2解:首先将图示信号分解为奇、偶函数,如下图(a)、(b)所示。……1……t-1(a)……1……0t-1(b)从图(a)可见为一个半波反对称偶函数。在这种情况下,其傅里级数展开式中将只含有余弦项,且只含奇次谐波分量而不含偶次谐波分量,即有:从图(b)

方波信号展开为傅里叶级数.doc
【例4.2-1】将下图所示方波信号展开为傅里叶级数。……0……t解:按题意方波信号在一个周期内的解析式为分别求得傅里叶系数:即:故得信号的傅里叶级数展开式为它只含有一、三、五、……等奇次谐波分量。【例4.2-2】将下图所示信号展开为傅里叶级数。2……0……t-2解:首先将图示信号分解为奇、偶函数,如下图(a)、(b)所示。……1……t-1(a)……1……0t-1(b)从图(a)可见为一个半波反对称偶函数。在这种情况下,其傅里级数展开式中将只含有余弦项,且只含奇次谐波分量而不含偶次谐波分量,即有:从图(b)

函数的傅里叶级数展开ppt课件.ppt
傅里叶级数和傅里叶变换前面所研究的幂级数是18世纪初英国数学家泰勒建立的,在分析学中,函数的泰勒展开起着很重要的作用,但是它对函数的要求很高,而且只能作局部逼近。19世纪法国数学家傅里叶研究热传导方程时建立了把函数展为三角级数的方法,其要求为函数黎曼可积或在反常积分意义下绝对可积,并且它可以整体逼近函数。物理学中最简单的波__谐波非正弦周期函数:矩形波56789一般地,二、三角级数三角函数系的正交性2.三角函数系的正交性13三、傅里叶级数系数1516傅里叶系数傅里叶级数四.傅里叶级数的收敛判别法注:21和

锯齿波傅里叶展开式PPT课件.ppt
例3-2-1感谢亲观看此幻灯片,此课件部分内容来源于网络,如有侵权请及时联系我们删除,谢谢配合!
