第三章图像的几何变换ppt课件.ppt

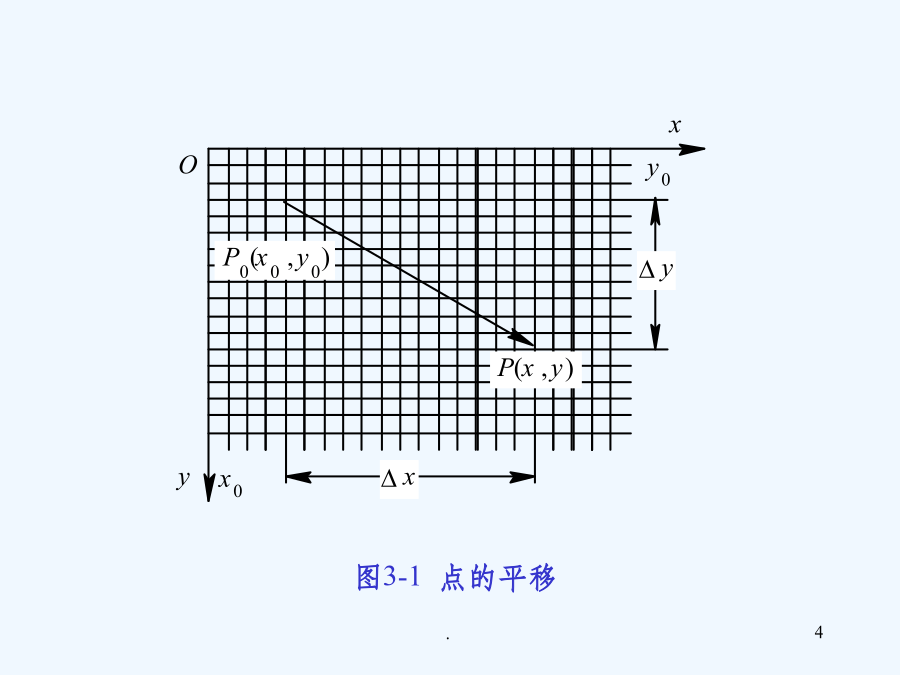
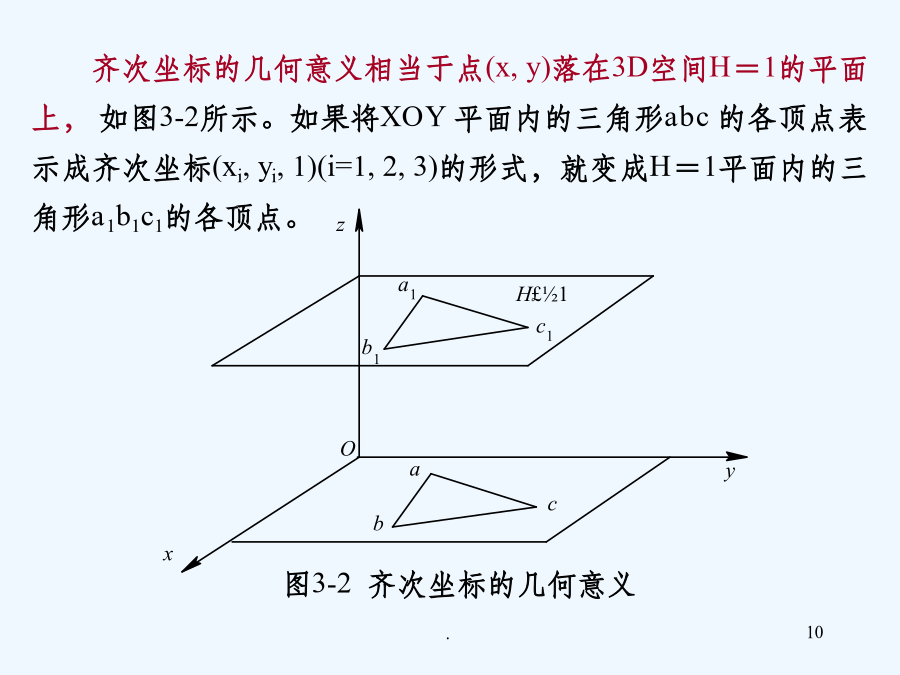
第三章图像的几何变换3.1几何变换基础为了能够用统一的矩阵线性变换形式来表示和实现这些常见的图像几何变换，需要引入一种新的坐标，即齐次坐标。
3.1.2齐次坐标
现设点P0(x0,y0)进行平移后，移到P(x,y)，其中x方向的平移量为Δx，y方向的平移量为Δy。那么，点P(x,y)的坐标为图3-1点的平移这个变换用矩阵的形式可以表示为要实现平移变换，平面上点的变换矩阵

需要使用2×3阶变换矩阵，取其形式为所以需要在点的坐标列矩阵［xy］T中引入第三个元素，增加一个附加坐标，扩展为3×1的列矩阵［xy1］T，这样用三维空间点（x,y,1）表示二维空间点（x,y），即采用一种特殊的坐标，可以实现平移变换，变换结果为通常将2×3阶矩阵扩充为3×3阶矩阵，以拓宽功能。下面再验证一下点P(x,y)按照3×3的变换矩阵T平移变换的结果。因此，2D图像中的点坐标(x,y)通常表示成齐次坐标（Hx,Hy,H），其中H表示非零的任意实数，当H＝1时，则(x,y,1)就称为点(x,y)的规范化齐次坐标。
由点的齐次坐标（Hx,Hy,H）求点的规范化齐次坐标(x,y,1)，可按如下公式进行：齐次坐标的几何意义相当于点(x,y)落在3D空间H＝1的平面上，如图3-2所示。如果将XOY平面内的三角形abc的各顶点表示成齐次坐标(xi,yi,1)(i=1,2,3)的形式，就变成H＝1平面内的三角形a1b1c1的各顶点。3.1.3二维图像几何变换的矩阵
利用齐次坐标改成3×3阶形式的变换矩阵，实现2D图像几何变换的基本变换的一般过程是：
1、将2×n阶的二维点集矩阵表示成齐次坐标
2、然后乘以相应的变换矩阵即可完成。即
变换后的点集矩阵=变换矩阵T×变换前的点集矩阵
（图像上各点的新齐次坐标）（图像上各点的原齐次坐标）设变换矩阵T为图像上各点的新齐次坐标规范化后的点集矩阵为3×3的阶矩阵T可以分成四个子矩阵。其中，这一子矩阵可使图像实现恒等、比例、反射（或镜像）、错切和旋转变换。［pq］T这一列矩阵可以使图像实现平移变换。［lm］这一行矩阵可以使图像实现透视变换，但当l=0，m=0时它无透视作用。［s］这一元素可以使图像实现全比例变换。例如，将图像进行全比例变换，即将齐次坐标 规范化后， 。由此可见，当s＞1时，图像按比例缩小；当0＜s＜1时，整个图像按比例放大；当s＝1时，图像大小不变。3.2图像比例缩放3.2图像比例缩放比例缩放前后两点P0(x0,y0)、P(x,y)之间的关系用矩阵形式可以表示为即首先讨论图像的比例缩小：
最简单的比例缩小是当fx=fy=1／2时，图像被缩到一半大小，图像缩小之后，因为承载的信息量小了，所以画布可相应缩小。此时，只需在原图像基础上，每行隔一个像素取一点，每隔一行进行操作，即取原图的偶（奇）数行和偶（奇）数列构成新的图像，如图3-4所示。如果图像按任意比例缩小，则需要计算选择的行和列。
如果M×N大小的原图像F(x，y)缩小为kM×kN大小（k<1）的新图像I(x，y)时，则
I(x,y)=F(int(c×x),int(c×y))
其中，c=1／k。由此公式可以构造出新图像，如图3-5所示。当fx≠fy(fx,fy＞0)时，图像不按比例缩小，这种操作因为在x方向和y方向的缩小比例不同，一定会带来图像的几何畸变。图像不按比例缩小的方法是：如果M×N大小的旧图像F(x，y)缩小为k1M×k2N（k1<1，k2<1）大小的新图像I(x，y)时，则
I(x,y)=F(int(c1×x),int(c2×y))其次讨论图像的比例放大：
在图像的放大操作中，则需要对尺寸放大后所多出来的空格填入适当的像素值，这是信息的估计问题，所以较图像的缩小要难一些。
当fx＝fy＝2时，图像被按全比例放大2倍，放大后图像中的

(0，0)像素对应于原图中的(0，0)像素；
(0，1)像素对应于原图中的(0，0.5)像素，该像素不存在，可以近似为(0，0)也可以近似(0，1)；
(0，2)像素对应于原图像中的(0，1)像素；
(1，0)像素对应于原图中的(0.5，0)，它的像素值近似于(0，0)或(1，0)像素；
(2，0)像素对应于原图中的(1，0)像素，依此类推。图3-6放大前的图像图3-7按最近邻域法放大两倍的图像一般地，按比例将原图像放大k倍时，如果按照最近邻域法则需要将一个像素值添在新图像的k×k的子块中，如图3-9所示。显然，如果放大倍数太大，按照这种方法处理会出现马赛克效应。图3-9按最近邻域法放大五倍的图像当fx≠fy(fx,fy＞0)时
图像在x方向和y方向不按比例放大，此时，这种操作由于x方向和y方向的放大倍数不同，一定带来图像的几何畸变。
放大的方法是将原图像的一个像素添到新图像的一个k1×k2的子块中去。灰度级插值处理