
结构力学第五章影响线PPT课件.ppt

lj****88







亲,该文档总共103页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

结构力学第五章影响线PPT课件.ppt
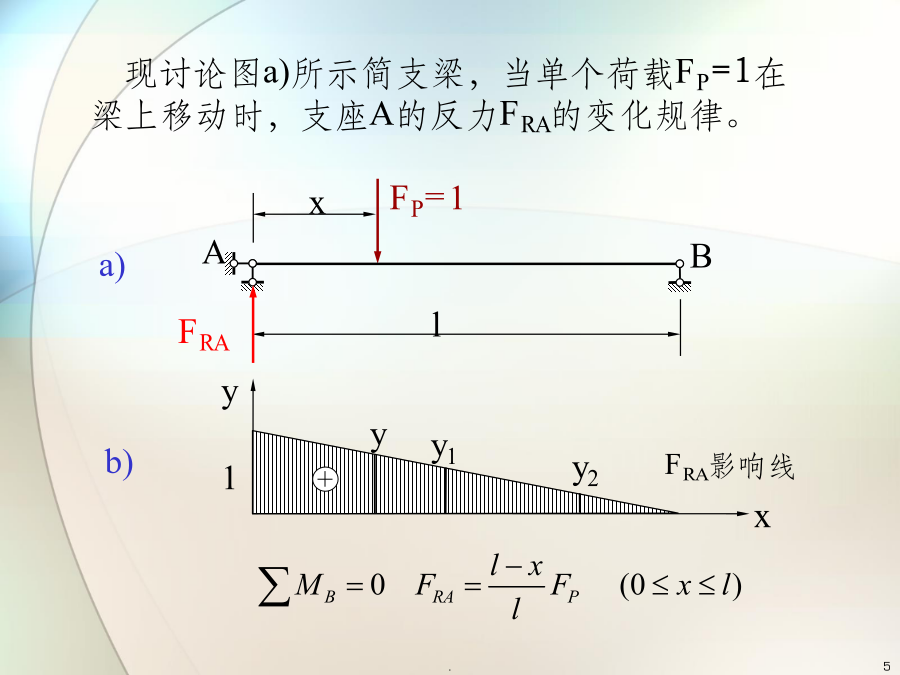
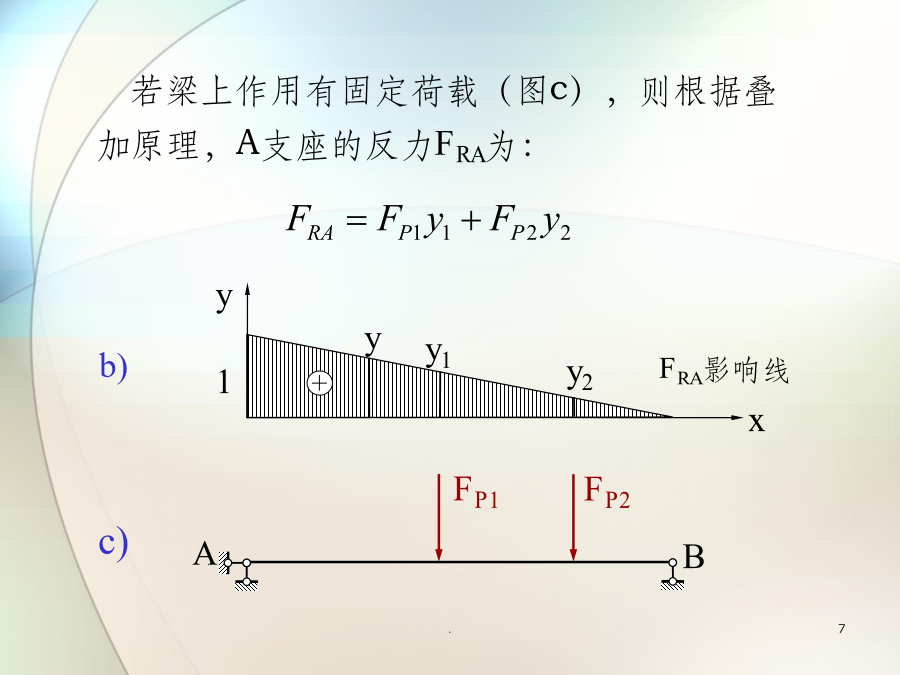
第五章影响线§5-1影响线的基本概念在移动载荷作用下,结构任意截面的内力(M、FQ、FN)和位移(△、θ)及支座反力均随移动荷载在结构上的位置变化而变化。2)对于给定的移动荷载组,简支梁AB上哪个截面的弯矩当移动荷载在什么位置时取得最大值?该问题是简支梁绝对最大弯矩的求解问题。FP=1在影响线图形中,横坐标x表示单位移动荷载在梁上的位置;纵坐标y表示当单位荷载在该位置时,影响系数的大小。B当单位集中移动荷载FP=1在结构上移动时,表示结构指定截面的某量值Z变化规律的曲线,称为Z的影响线。量值Z可以是截面内

结构力学机动法作影响线ppt课件.ppt
——运用虚位移原理,把作内力或支座反力影响线的静力问题转化为作位移图的几何问题。a、求某点某量值的影响线,就把相应的约束去掉,用正方向的力来代替(称为真实的力状态);[例1]试用机动法作简支梁C点的弯矩和剪力的影响线。作剪力FQC的影响线[例2]试用机动法作静定多跨梁的MK,FQK,MC,FQE,FRD的影响线。FQK的影响线MC的影响线FQE的影响线FRD的影响线结束感谢亲观看此幻灯片,此课件部分内容来源于网络,如有侵权请及时联系我们删除,谢谢配合!
结构力学机动法作影响线PPT课件.ppt
——运用虚位移原理,把作内力或支座反力影响线的静力问题转化为作位移图的几何问题。a、求某点某量值的影响线,就把相应的约束去掉,用正方向的力来代替(称为真实的力状态);[例1]试用机动法作简支梁C点的弯矩和剪力的影响线。作剪力FQC的影响线[例2]试用机动法作静定多跨梁的MK,FQK,MC,FQE,FRD的影响线。FQK的影响线MC的影响线FQE的影响线FRD的影响线结束

结构力学-第5章-影响线ppt课件.ppt
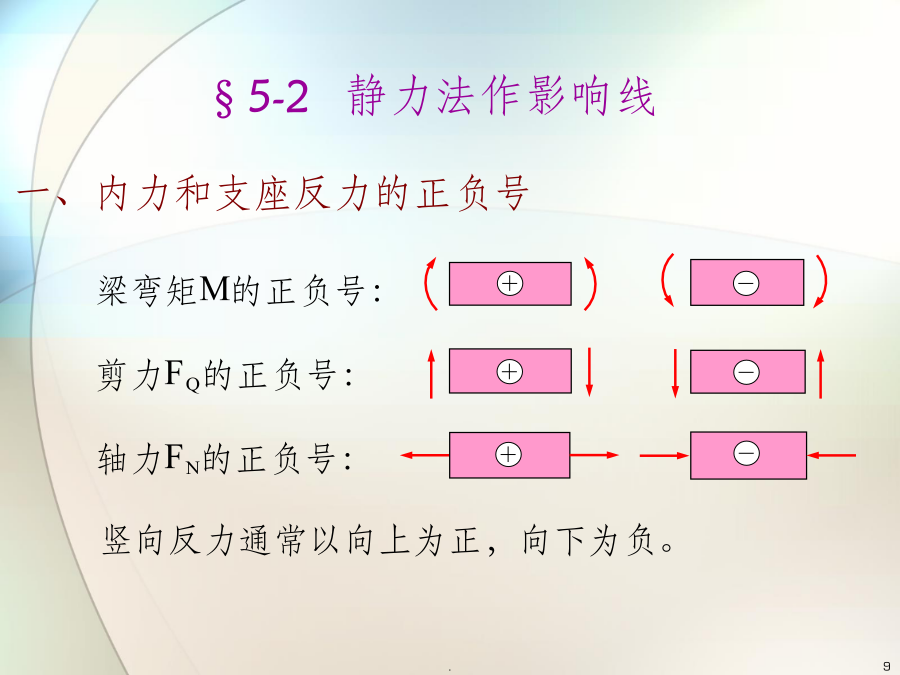
一、移动荷载的概念1.影响线的绘制结构上某截面的内力或支座反力随移动荷载位置变化而变化的规律。2.影响线的应用确定移动荷载的最不利位置,并求出支座反力或内力的最大值,作为结构设计的依据。§5.2静力法作简支梁的影响线一、静力法作影响线的原理和步骤1.选择坐标系,定坐标原点,并用变量x表示单位移动荷载的作用位置;2.列出某截面内力或支座反力关于x的静力平衡方程,并注明变量x的取值范围;3.根据影响线方程绘出影响线。注意:(1)内力或支座反力的正负号规定:弯矩和剪力同前,竖向支座反力以向上为正;(2)量值的正

结构力学——影响线 PPT.ppt
学习内容影响线的概念,用静力法和机动法作静定梁的影响线,影响量的计算和最不利荷载位置的确定,连续梁影响线形状的确定和最不利活荷载位置的确定。第一节影响线的概念第一节影响线的概念第一节影响线的概念第二节静力法作静定梁的影响线第二节静力法作静定梁的影响线第二节静力法作静定梁的影响线第二节静力法作静定梁的影响线第二节静力法作静定梁的影响线10第二节静力法作静定梁的影响线第二节静力法作静定梁的影响线第二节静力法作静定梁的影响线第二节静力法作静定梁的影响线第二节静力法作静定梁的影响线第二节静力法作单跨静定梁的影响线
