第1章--几何机动分析--结构力学ppt课件.ppt

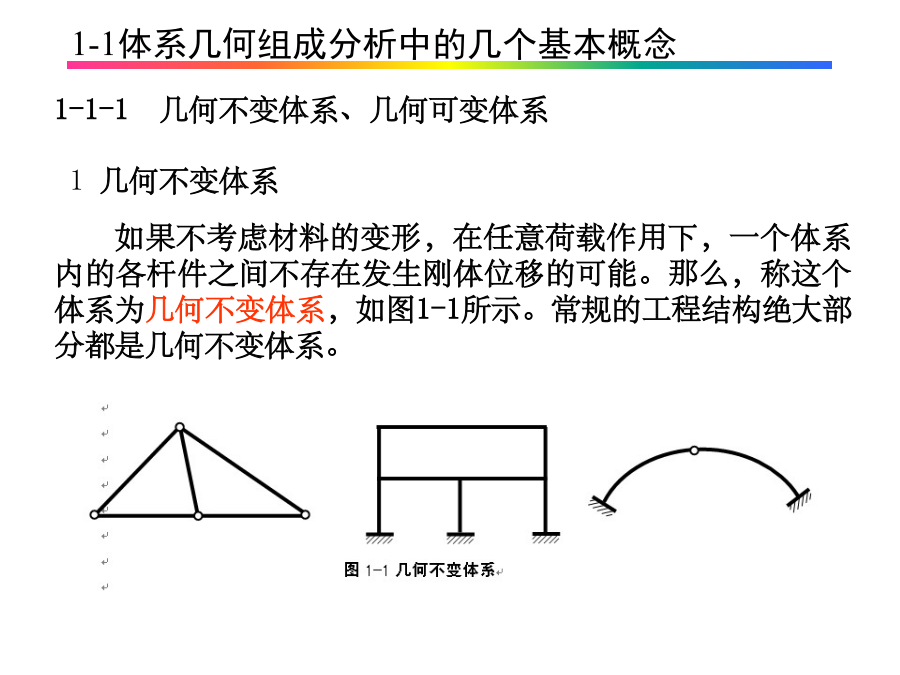
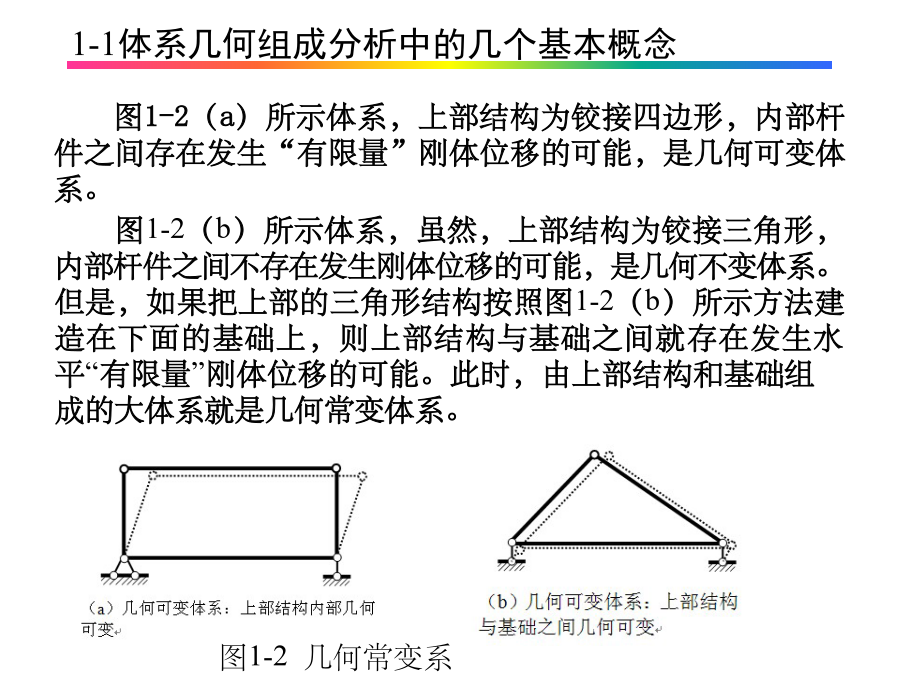
第1章杆件体系的几何组成分析1-1-1几何不变体系、几何可变体系2几何可变体系图1-2（a）所示体系，上部结构为铰接四边形，内部杆件之间存在发生“有限量”刚体位移的可能，是几何可变体系。几何常变体系只能在特定荷载下维持平衡，在一般荷载作用下均可能发生运动，因此几何常变体系不能作为常规的工程结构。1-1-2刚片、自由度和约束在几何组成分析中，在保证与体系其它部分连接形式不变的前提下，刚片是可以替换的。因为，这样的替换不改变体系的自由度和约束的情况。因此，体系的几何组成结论不变。例如：图1-4a中的刚片Ⅰ是一根折杆，与体系的其它部分用铰连接。可以用最简单的直杆来替换。同理，刚片Ⅱ也可以用直杆替换。如图1-4所示。这样的替换会使结构的分析变得简单。2自由度例如：图1-5（a）所示的两个刚片组成的体系。两个刚片之间可以发生相对水平运动、相对竖向运动和相对转动。因此，体系的内部自由度为3。同理，在图1-5（b）所示的点A和基础组成的体系中，点A和基础之间可以发生相对水平运动和相对竖向运动。因此，体系的内部自由度为2；当然，在刚片和基础组成的体系中，其内部自由度为3（图1-5（c））3约束由此可见，一根链杆相当于1个约束，可减少1个自由度。（2）铰结点:一种是单铰结点，另一种是复铰结点。上图所示为刚片AB、BC、BD组成的体系。若没有铰B，则体系内部共有6个自由度。用铰结点连接后，体系的自由度为2（任意两个刚片相对于另一个刚片的转角），减少的自由度数目为4。若用m表示复铰结点连接的刚片数，用n表示复铰结点减少的自由度数目，则不难得出关系式：n=2(m-1)。因此，连接m个刚片的复铰结点相当于m-1个单铰结点。与“链杆”的定义相似，“铰”的定义也是广泛的。铰的约束作用是使它所联系的刚片只能绕其转动。因此，理论力学中的“瞬时转动中心”在广义上也是铰。因为是两个杆件延长线的交点，故称其为虚铰。（3）刚结点：有单刚结点和复刚结点两种1-2-1两个刚片用一个铰和一根链杆连接组成的体系再考察图1-9（c）和图1-9（d）两种情况。若链杆1通过铰A，则起不到减少自由度的作用，体系仍为几何可变体系；若再增加链杆2，很明显，该链杆对体系的几何稳定性不起作用。这种不能较少体系自由度的约束称为多余约束。多余约束对于保持体系的几何稳定性来说是不必要的，但后面将会看到，多余约束对于改善结构的受力、增加结构的安全度等方面来说是需要的。由上面的分析，可以得出以下几何不变体系的组成规律。规律2两个本身无多余约束的刚片用三根既不相互平行，（延长线）又不相交于一点链杆连接，则组成的体系为几何不变体系，且无多余约束。若三根链杆的延长线交于一点（图1-10（b）），则两个刚片将以这个交点作为瞬时转动中心，发生微小的相对转动。转动后，三根链杆的延长线便不再交于一点。因此，该体系为几何瞬变体系。若三根链杆（图1-10（c））交于一点（实铰），很明显，转动将继续下去，体系为几何可变体系。图1-11（c）中，三根链杆平行且等长，但链杆从刚片的两侧连出，两个刚片发生微小相对水平位移后，三根链杆将不在全平行，体系变成几何不变体系。因此，原体系也为几何瞬变体系。1-2-3三个刚片用三个铰连接组成的体系规律3三个本身无多余约束的刚片，用不在一条直线上的三个铰两两相连，则组成的体系为几何不变体系，且无多余约束。1一个铰在无穷远的情况图（a）中，虚铰O(Ⅰ,Ⅱ)在无穷远处，另外两个铰的连线与无穷远方向不平行，所以体系为几何不变体系。若另外两个铰的连线与无穷远方向平行，则体系为几何瞬变体系（图（b））。特殊地，若组成无穷远虚铰的两根链杆平行且等长，则体系为几何常变体系（图（c））。2两个铰在无穷远的情况图1-14(a)所示体系，有两个无穷远虚铰和一个有限位置的虚铰，体系为几何不变体系。若两个无穷远虚铰的四根链杆平行，则可认为在该方向上有一个无穷远虚铰，这个铰与有限位置的虚铰当然共线，因此，体系为瞬变体系（图1-14（b））。更进一步，若这四根链杆平行且等长，则体系为常变体系（图1-14（c））。3三个铰在无穷远的情况1-2-4二元体规律几何组成分析时，在一个体系中正确判断哪部分是二元体是非常有用的。初学者在判断时也比较容易出错。去掉二元体的情况与此类似。于是得出如下二元体规律:【例题1-1】分析图1-17（a）所示体系的几何组成。【例题1-2】分析图1-18（a）所示体系的几何组成。图1-18（b）所示体系，依次去掉二元体后，得到图1-18（c）所示体系。很明显，该体系有一个自由度。所以原体系也是有一个自由度的常变体系。【例题1-3】分析图1-21（a）所示体系的几何组成。【例题1-4】分析图1-22（a）所示体系的几何组成。读者可以试着选择其它杆件作为刚片进行分析。【例题1-5】分析图1-24（a