常见优化模型PPT课件.ppt

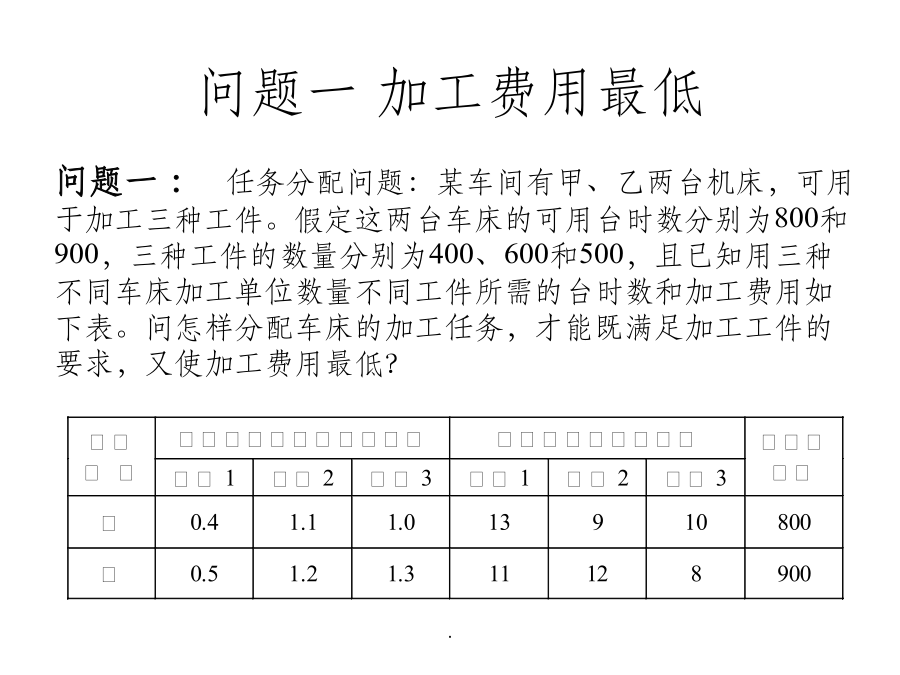
常见优化模型常见优化模型线性规划问题一加工费用最低用MATLAB优化工具箱解线性规划3、模型：minz=cX

解编写M文件xxgh1.m如下：
c=[-0.4-0.28-0.32-0.72-0.64-0.6];
A=[0.010.010.010.030.030.03;0.02000.0500;00.02000.050;000.03000.08];
b=[850;700;100;900];
Aeq=[];beq=[];
vlb=[0;0;0;0;0;0];vub=[];
[x,fval]=linprog(c,A,b,Aeq,beq,vlb,vub)

解:编写M文件xxgh2.m如下：
c=[634];
A=[010];
b=[50];
Aeq=[111];
beq=[120];
vlb=[30;0;20];
[x,fval]=linprog(c,A,b,Aeq,beq,vlb)
投资的收益和风险二、基本假设和符号规定三、模型的建立与分析.四、模型1的求解a=0;
while(1.1-a)>1
c=[-0.05-0.27-0.19-0.185-0.185];
Aeq=[11.011.021.0451.065];beq=[1];
A=[00.025000;000.01500;0000.0550;00000.026];
b=[a;a;a;a];
vlb=[0,0,0,0,0];vub=[];
[x,val]=linprog(c,A,b,Aeq,beq,vlb,vub);
a
x=x'
Q=-val
plot(a,Q,'.')，axis([00.100.5])，holdon
a=a+0.001;
end
xlabel('a'),ylabel('Q')计算结果：五、结果分析定义如果目标函数或约束条件中至少有一个是非线性函数时的最优化问题就叫做非线性规划问题．应用实例：供应与选址（一）、建立模型（二）使用临时料场的情形（三）改建两个新料场的情形