线性规划问题的数学模型ppt课件.ppt

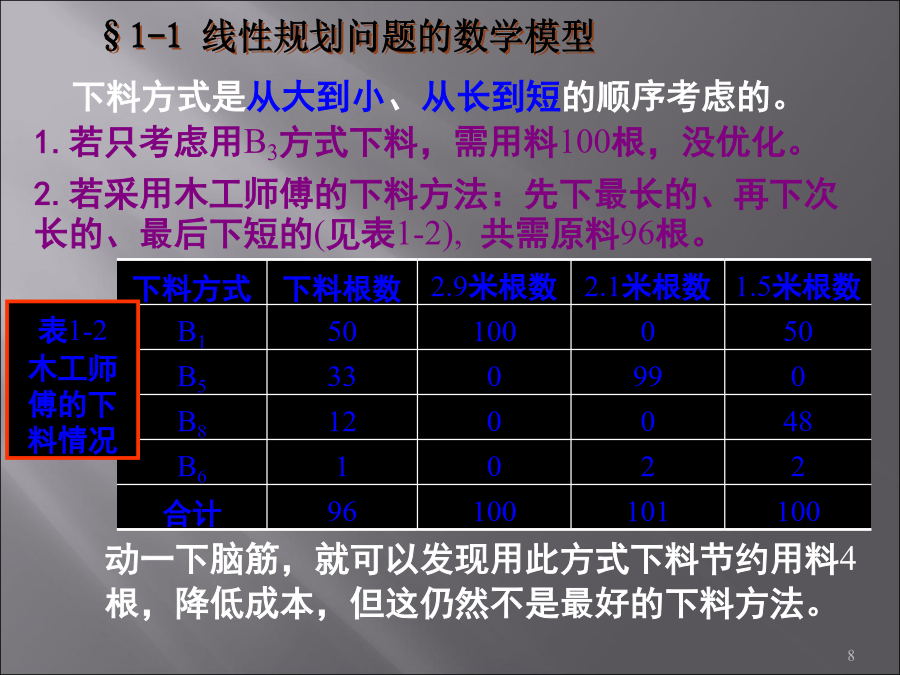
第一篇线性规划模型及应用Mathematicalmodelingmethod线性规划模型及应用10第1章线性规划问题的数学模型及其解的性质背景介绍某工厂生产一种型号的机床，每台机床上需要2.9米、2.1米和1.5米长的三种轴各一根，这些轴需要用同一种圆钢制作,圆钢的长度为7.4米。如果要生产100台机床，应如何下料，才能使得用料最省？分析下料方式是从大到小、从长到短的顺序考虑的。3.若要我们安排下料,暂不排除8种下料方式中的任何一种,通过建立数学模型进行求解,寻找最好的下料方案。用LINGO10.0软件求解，
程序如下：下料问题是在经济和管理中经常遇到的问题，引例是条材下料问题、此外还有板材下料问题（如五金厂生产保险柜的下料、服装厂下料等）或者更复杂的下料问题。请考虑一下，下料方式能不能用计算机来设计更合理？本问题能不能将目标函数确定为余料最少，为什么？这都是值得读者思考的问题。例1.某工厂生产一型号机床，每台机床上需要2.9米、2.1米和1.5米长的三种轴分别为1、2、1根，这些轴需要用同一种圆钢制作,圆钢的长度为7.4米。如果要生产100台机床，应如何下料，才能使得用料最省？★一般下料问题:设用某种材料(条材或板材)下零件A1,A2,…,Am的毛坯，据过去的经验，在一件原料上有B1,B2,…,Bn共n种不同的下料方式，每种合理的下料方式可得各种毛坯个数及每种零件的需要量如表1-3。问:
怎样安排下料方式,使得既满足需要,又使得用料最省？则建立线性规划问题数学模型：从我们所建立的数学模型来看，目标函数是决策变量的线性函数、约束条件是决策变量的线性等式或线性不等式,故我们称此为线性规划(LinearProgramming,
简记为LP)模型。二、资源合理利用(资源的最优配置)问题解：★一般地,用m种原料A1,A2,…,Am可以生产n种产品B1,B2,…,Bn.现有原料数ai(可利用资源数量)、每单位产品所需原料数cij(消耗系数)及每单位产品可得利润bj(i=1,2,…,m;j=1,2,…,n)如表1-5。问：应如何组织生产才能使总利润最大？解:设xj表示生产产品Bj的数量(j=1,2,…,n)，则可建立线性规划数学模型：表1-6配料（食谱）问题的数据min=0.2*x1+0.7*x2+0.4*x3+0.3*x4+0.5*x5；
0.3*x1+2*x2+x3+0.6*x4+1.8*x5>=70；
0.1*x1+0.05*x2+0.02*x3+0.2*x4+0.05*x5>=3；
0.05*x1+0.1*x2+0.02*x3+0.2*x4+0.08*x5>=10；★一般地,用n种原料B1,B2,…,Bn制成具有m种成分A1,A2,…,Am的产品,其所含的万分分别不少于a1,a2,…,am,各种原料的单价bj以及各种原料所含成分的数量cij(i=1,2,…,m;j=1,2,…,n)如表1-7。问：应如何配料才能使总成本最小？解:设需要原料Bj的数量为xj单位(j=1,2,…,n)，则可建立线性规划数学模型：表1-8运输问题的数据解:设砖厂Ai供应建筑工地Bj砖块的数量为xij(i=1,2;j=1,2,3)(j=1,2,…,n)，则可建立线性规划数学模型：★一般地,某种物资有m个产地:A1,A2,…,Am联合供应n个销地B1,B2,…,Bn,各产地产量ai各销地销量bj以及各产地到各销地的单位运价cij(i=1,2,…,m;j=1,2,…,n)如表1-9。问：应如何组织运输才能使得总运费最省？解:设xij表示产地Ai供应销地Bj的数量(i=1,2,…,m;
j=1,2,…,n)。§1-1线性规划问题的数学模型★类似的模型还有农作物布局问题：解:设xij表示土地Bj种植农作物Ai的面积(i=1,2,…,m;
j=1,2,…,n)。满足所有约束条件的线性规划问题的数学模型是描述实际问题的抽象数学形式，它反映了客观事物数量间的本质规律。解:例6如果该问题是产品B的单位利润为4元，则该线性规划问题的数学模型是：例7、用图解法求解线性规划问题：例8用图解法求解线性规划问题：通过以上举例，我们可以看出线性规划解的情况：一、软件简介>>LINGO可用于求解
线性规划（LP—LinearProgramming）
和整数规划（IP—IntegerProgramming）问题，
也可用于求解
非线性规划（NLP—NoLinearProgramming）
和二次规则（QP—QuaraticProgramming），
不同版本的LINGO对求解规模有不同的限制。虽然LINGO不能直接求解目标规划问题，但用序贯式算法可分解成一个个LINGO能解决的规划问题。要学好用好这个软件最好的办法就是学习他们自带的HELP文件，也可以参考其他关于LINGO软件的书籍。>