
线段和差的最值问题.ppt

天马****23










亲,该文档总共31页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

线段和差的最值问题.pptx
线段和差的最值问题解题策略两条线段和旳最小值两点之间,线段最短线段和差的最值问题解题策略一、求两条线段之和的最小值例1:在△ABC中,AC=BC=2,∠ACB=90O,D是BC边旳中点,E是AB上旳一动点,则EC+ED旳最小值为。例2:△ABC中,AC=3,BC=4,AB=5,试在AB上找一点P,在BC上取一点M,使CP+PM旳值最小,并求出这个最小值。例1、例2中旳最小值问题,所涉及到旳途径,虽然都是由两条线段连接而成,但是途径中旳动点与定点旳个数不同,例1中旳途径为“定点→动点→定点”,是两个定点一种

线段和差的最值问题.ppt
线段和差的最值问题解题策略两条线段和的最小值两点之间,线段最短线段和差的最值问题解题策略一、求两条线段之和的最小值例1:在△ABC中,AC=BC=2,∠ACB=90O,D是BC边的中点,E是AB上的一动点,则EC+ED的最小值为。例2:△ABC中,AC=3,BC=4,AB=5,试在AB上找一点P,在BC上取一点M,使CP+PM的值最小,并求出这个最小值。例1、例2中的最小值问题,所涉及到的路径,虽然都是由两条线段连接而成,但是路径中的动点与定点的个数不同,例1中的路径为“定点→动点→定点”,是两个定点一个

线段和差的最值问题.ppt
中考专题复习2.几何最值问题的基本原理。①两点之间线段最短②垂线段最短③三角形两边之差小于第三边④利用函数关系求最值一、两条线段和的最小值一、求两条线段之和的最小值例1:在△ABC中,AC=BC=2,∠ACB=90O,D是BC边的中点,E是AB上的一动点,则EC+ED的最小值为。2、抛物线在坐标系中的位置如图:对在其称轴上找一点P,使得△PBC的周长最小,请求出点P的坐标.线段和差的最值问题解题策略练习:已知二次函数图像的顶点坐标为C(3,-2),且在x轴上截得的线段AB的长为4,在y轴上有一点P,使△A

线段和差最值问题.pdf
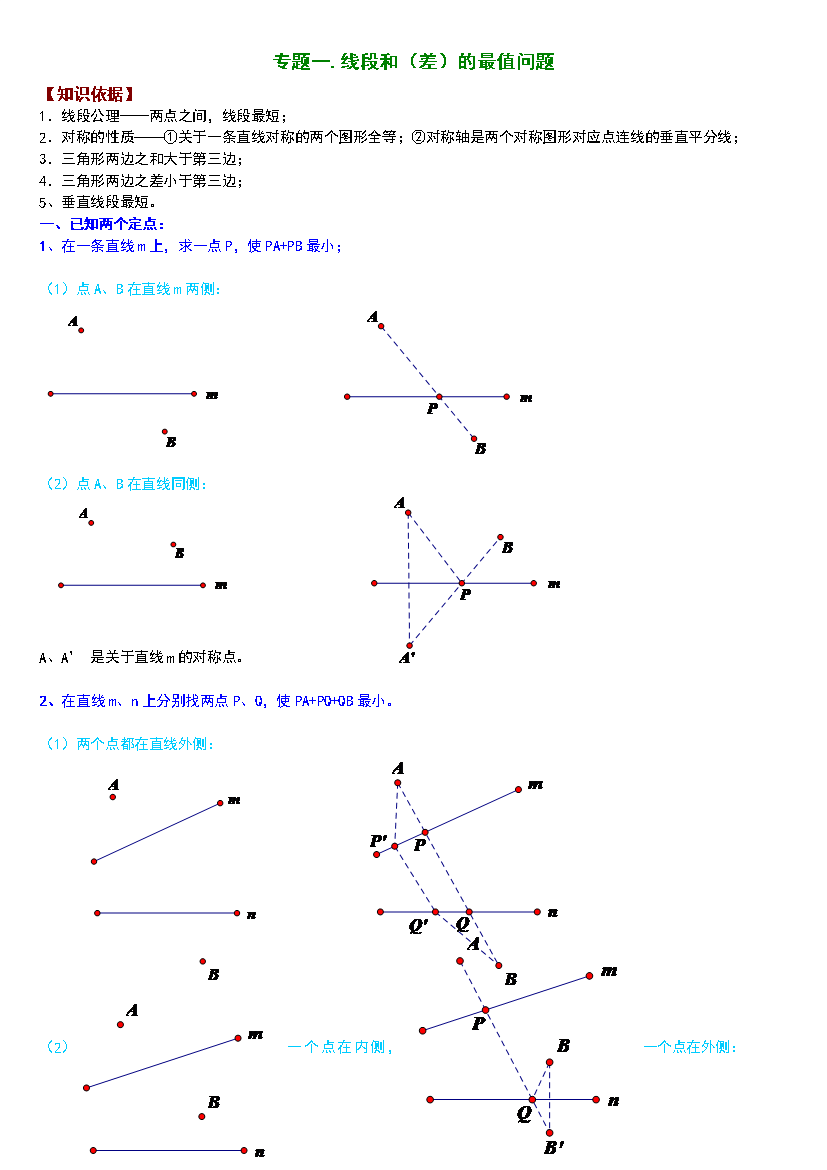
.专题一.线段和〔差的最值问题[知识依据]1.线段公理——两点之间线段最短;2.对称的性质——①关于一条直线对称的两个图形全等;②对称轴是两个对称图形对应点连线的垂直平分线;3.三角形两边之和大于第三边;4.三角形两边之差小于第三边;5、垂直线段最短。一、已知两个定点:1、在一条直线m上求一点P使PA+PB最小;〔1点A、
线段和差最值问题.doc
专题一.线段和(差)的最值问题【知识依据】线段公理——两点之间,线段最短;对称的性质——①关于一条直线对称的两个图形全等;②对称轴是两个对称图形对应点连线的垂直平分线;三角形两边之和大于第三边;三角形两边之差小于第三边;垂直线段最短。一、已知两个定点:1、在一条直线m上,求一点P,使PA+PB最小;(1)点A、B在直线m两侧:(2)点A、B在直线同侧:A、A’是关于直线m的对称点。2、在直线m、n上分别找两点P、Q,使PA+PQ+QB最小。(1)两个点都在直线外侧:(2)一个点在内侧,一个点在外侧:(3)
