
第讲相关分析与回归分析教案.ppt

lj****88






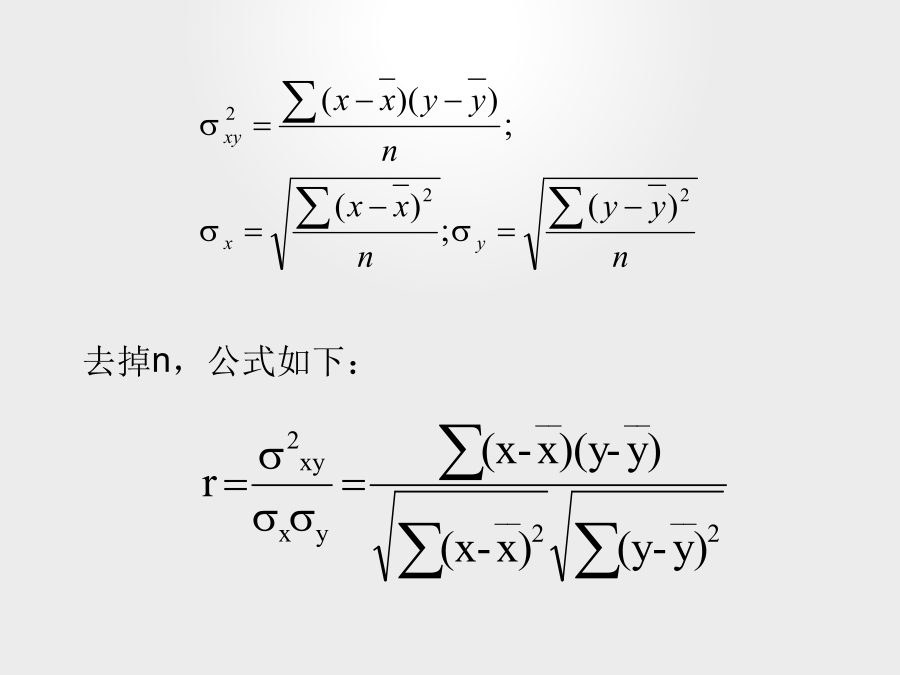
亲,该文档总共50页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

第讲相关分析与回归分析教案.ppt
相关分析与回归分析章节提纲:第一、二节-相关分析概述-相关关系测定变量间关系指数函数三、相关关系相关系数是度量两个变量之间线性相关的方向和强度的测度,常用的度量指标是皮尔逊(Pearson)相关系数【专栏】在相关分析中,定性分析或经济理论分析重要吗?相关系数(CorrelationCoefficient)1.总体相关系数(Populationcorrelationcoefficient)去掉n,公式如下:度量线性关系的强度和方向:1)r=0--无线性关系,或很弱2)若绝对值较大--线性关系较强3)符号正负

第讲相关分析与回归分析教案.ppt
相关分析与回归分析章节提纲:第一、二节-相关分析概述-相关关系测定变量间关系指数函数三、相关关系相关系数是度量两个变量之间线性相关的方向和强度的测度,常用的度量指标是皮尔逊(Pearson)相关系数【专栏】在相关分析中,定性分析或经济理论分析重要吗?相关系数(CorrelationCoefficient)1.总体相关系数(Populationcorrelationcoefficient)去掉n,公式如下:度量线性关系的强度和方向:1)r=0--无线性关系,或很弱2)若绝对值较大--线性关系较强3)符号正负

第8讲----相关分析和回归分析.ppt
第8讲相关分析和回归分析一、相关分析二、回归分析相关系数示意图相关系数示意图相关系数(correlationcoefficient),对于正态分布资料,选择积差相关系数,又称Pearson相关系数.对于非正态分布资料,选择等级相关系数(Spearman或Kendall相关系数).【例1】相关分析.sav分析年龄和片段长度的相关性回归分析(Regression)是一种应用极为广泛的数量分析方法。它用于考察一个变量(因变量)与其余变量(自变量)之间的数量关系,并通过回归方程的形式反映这种关系,进而为控制和预测

第8讲----相关分析和回归分析.ppt
第8讲相关分析和回归分析一、相关分析二、回归分析相关系数示意图相关系数示意图相关系数(correlationcoefficient),对于正态分布资料,选择积差相关系数,又称Pearson相关系数.对于非正态分布资料,选择等级相关系数(Spearman或Kendall相关系数).【例1】相关分析.sav分析年龄和片段长度的相关性回归分析(Regression)是一种应用极为广泛的数量分析方法。它用于考察一个变量(因变量)与其余变量(自变量)之间的数量关系,并通过回归方程的形式反映这种关系,进而为控制和预测

第二讲 相关分析与回归分析.doc
相关分析与回归分析--第二讲相关分析与回归分析第一节相关分析1.1变量的相关性1.变量的相关性分两种,一种是研究两个变量X与Y的相关性。本节只研究前者,即两个变量之间的相关性;。2.两个变量X与Y的相关性研究,是探讨这两个变量之间的关系密切到什么程度,能否给出一个定量的指标。这个问题的难处在于“关系”二字,从数学角度看,两个变量X、Y之间的关系具有无限的可能性,一个比较现实的想法是:确立一种“样板”关系,然后把X、Y的实际关系与“样板”关系比较,看它们“像”到了什么程度,给出一个定量指标。3.取什么关系做
