
双曲线及其标准方程市公开课一等奖省赛课获奖PPT课件.pptx

lj****88








亲,该文档总共24页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

双曲线及其标准方程市公开课一等奖省赛课获奖PPT课件.pptx
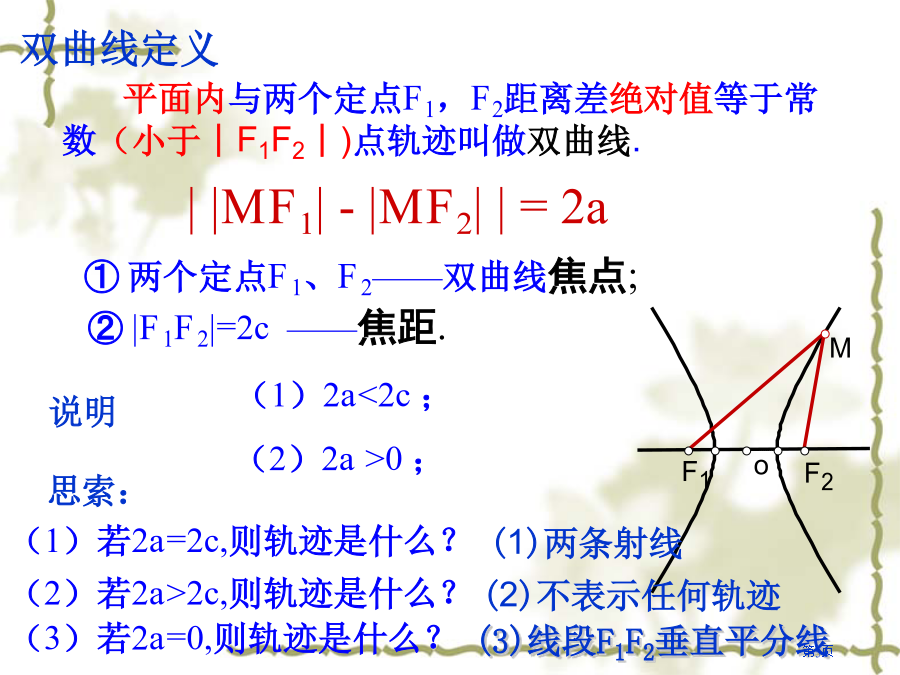
2.3.1双曲线及其标准方程1.椭圆定义是怎样?①如图(A),①两个定点F1、F2——双曲线焦点;此即为焦点在x轴上双曲线标准方程看前系数,哪一个为正,则在哪一个轴上1.判断:(正确打“√”,错误打“×”)(1)在双曲线标准方程中,a,b,c之间关系同椭圆中a,b,c之间关系相同.()(2)点A(1,0),B(-1,0),若|AC|-|BC|=2,则点C轨迹是双曲线.()DA方法归纳求双曲线标准方程与求椭圆标准方程方法相同,能够先依据其焦点位置设出标准方程形式,(先定位再定量)然后用待定系数法求出a,b值

双曲线及其标准方程(一)PPT课件市公开课一等奖省赛课获奖PPT课件.pptx
2.3.1双曲线及其标准方程(一)1.椭圆定义巴西利亚大教堂罗兰导航系统原理学习目标画双曲线画双曲线①如图(A),①两个定点F1、F2——双曲线焦点;(1)2a<2c;(1)F1F2延长线和反向延长线(两条射线)注:(1)当|MF1|-|MF2|=2a时,点p轨迹为近F2一支.(2)当|MF1|-|MF2|=-2a时,点p轨迹为近F1一支.探究:(3)已知A(-5,0),B(5,0),M点到A,B两点距离之差绝对值为12,则M点轨迹是什么?此即为焦点在x轴上双曲线标准方程问题:怎样判断双曲线焦点在哪个轴上

双曲线的定义及其标准方程市公开课一等奖省赛课获奖PPT课件.pptx
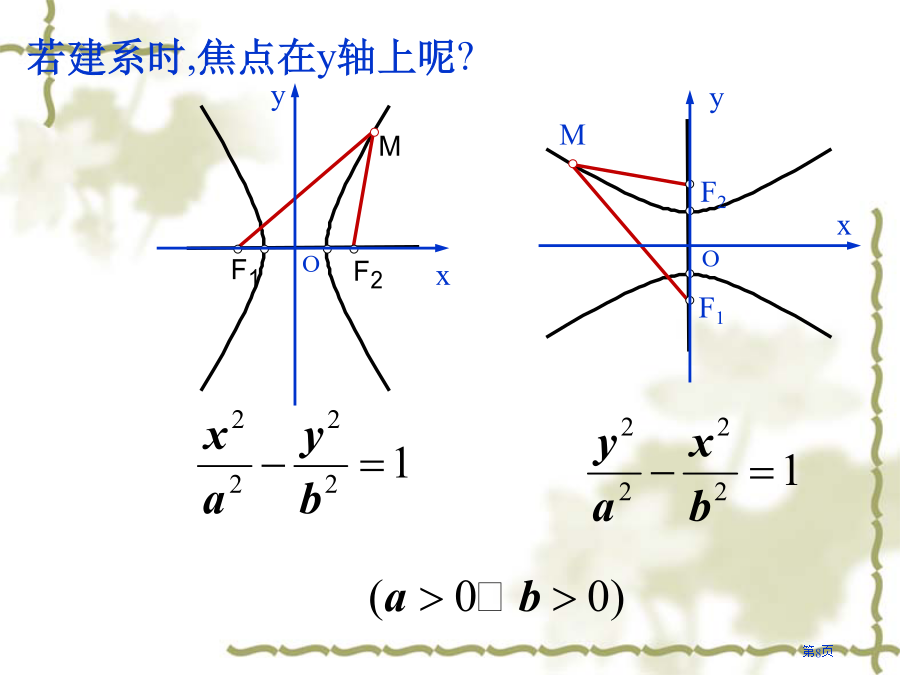
双曲线及其标准方程1.椭圆定义①如图(A),双曲线在生活中☆.☆①两个定点F1、F2——双曲线焦点;此即为焦点在x轴上双曲线标准方程看前系数,哪一个为正,则在哪一个轴上使A、B两点在x轴上,而且点O与线段AB中点重合答:再增设一个观察点C,利用B、C(或A、C)两处测得爆炸声时间差,能够求出另一个双曲线方程,解这两个方程组成方程组,就能确定爆炸点准确位置.这是双曲线一个主要应用.例2:假如方程表示双曲线,求m取值范围.******小结******感激您聆听!THANKSFORYOURKINDATTENTI

双曲线的准线方程市公开课一等奖省赛课获奖PPT课件.pptx
1、了解圆锥曲线统一定义。平面内到两定点F1、F2距离之差绝对值等于常数2a(2a<|F1F2|)点轨迹。表示式||PF1|-|PF2||=2a(2a<|F1F2|)典例引路类比归纳平面内到一定点F与到一条定直线l距离之比为常数e点轨迹:(点F不在直线l上)依据图形对称性可知,椭圆和双曲线都有两条准线.练习1:求以下曲线焦点坐标、准线方程和离心率已知椭圆短轴长是2,长轴长是短轴长2倍,则其中心到准线距离是()2.设双曲线两条准线把两焦点间线段三等分,则此双曲线离心率为()练习3:椭圆上一点P到一个焦点F1

椭圆及其标准方程复习课市公开课一等奖省赛课获奖PPT课件.pptx
椭圆及其标准方程(复习课)思索:例2:求满足以下条件椭圆标准方程:设F1,F2为定点,|F1F2|=6,动点M满足|MF1|+|MF2|=6,则动点轨迹是()2.假如方程x2+ky2=2表示焦点在y轴上椭圆,则k取值范围是_______.例1、求满足以下条件椭圆标准方程:巩固提升:2.已知椭圆方程为:,则a=_____,b=_______,c=_______,焦点坐标为:____________焦距等于______;若CD为过左焦点F1弦,则∆F2CD周长为____
