
平面直角坐标系中的伸缩变换.ppt

lj****88







亲,该文档总共17页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

平面直角坐标系中的伸缩变换.ppt
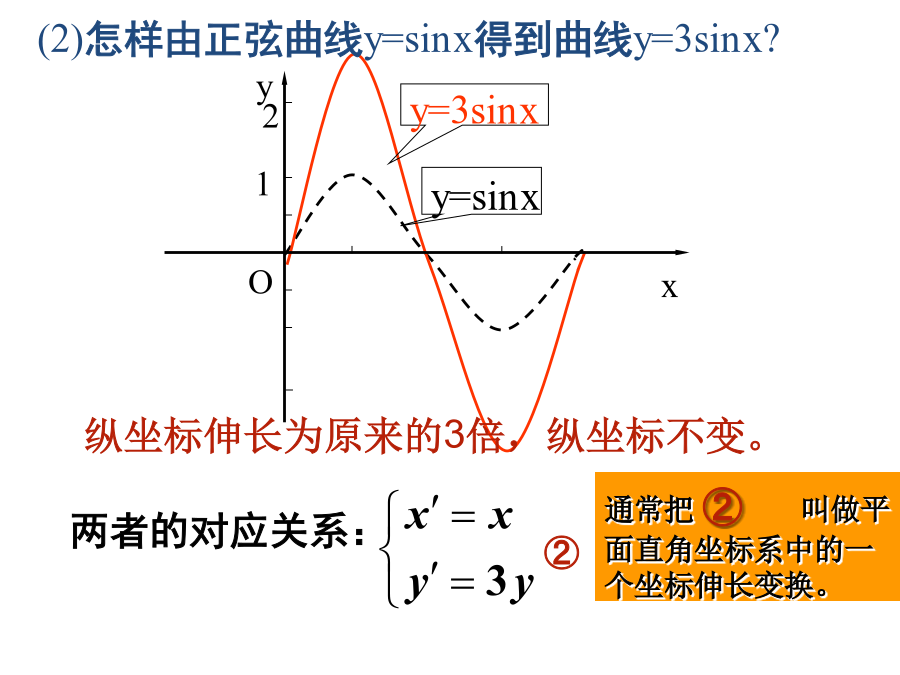
一、课题引入问题2:怎样由正弦曲线y=sinx得到曲线y=3sinx?写出其坐标变换。(插入几何画板)思考二:从平面直角坐标系中的点的对应关系出发,保持横坐标不变,纵坐标伸长为比原来的3倍的实质是什么?定义:设P(x,y)是平面直角坐标系中任意一点,在变换三、例题讲解思考:在伸缩下变换公式下,椭圆是否可以变成圆?抛物线,双曲线变成什么曲线?四、课堂小结:课后作业:思考题:

平面直角坐标系中的伸缩变换.ppt
一、课题引入问题2:怎样由正弦曲线y=sinx得到曲线y=3sinx?写出其坐标变换。(插入几何画板)思考二:从平面直角坐标系中的点的对应关系出发,保持横坐标不变,纵坐标伸长为比原来的3倍的实质是什么?定义:设P(x,y)是平面直角坐标系中任意一点,在变换三、例题讲解思考:在伸缩下变换公式下,椭圆是否可以变成圆?抛物线,双曲线变成什么曲线?四、课堂小结:课后作业:思考题:

平面直角坐标系中的伸缩变换.docx
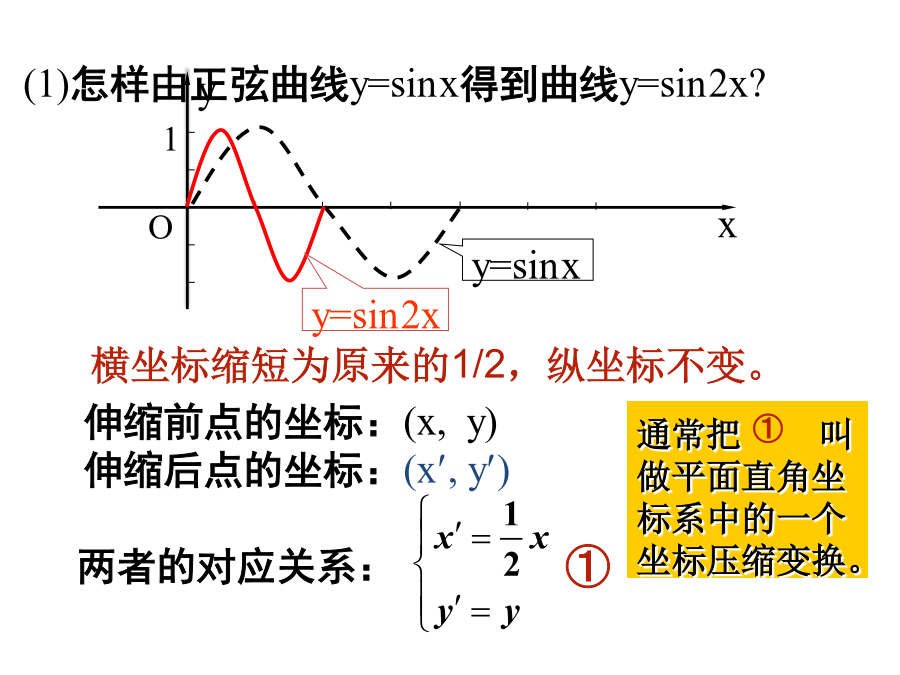
课题:2、平面直角坐标系中的伸缩变换教学目标:知识与技能:平面直角坐标系中的坐标变换过程与方法:体会坐标变换的作用情感、态度与价值观:通过观察、探索、发现的创造性过程,培养创新意识教学重点:理解平面直角坐标系中的坐标变换、伸缩变换教学难点:会用坐标变换、伸缩变换解决实际问题授课类型:新授课教学措施与方法:启发、诱导发现教学.教学过程:一、阅读教材P4—P8问题探究1:怎样由正弦曲线得到曲线?思考:“保持纵坐标不变横坐标缩为原来的一半”的实质是什么?问题探究2:怎样由正弦曲线得到曲线?思考:“保持横坐标不变

平面直角坐标系中的伸缩变换.ppt
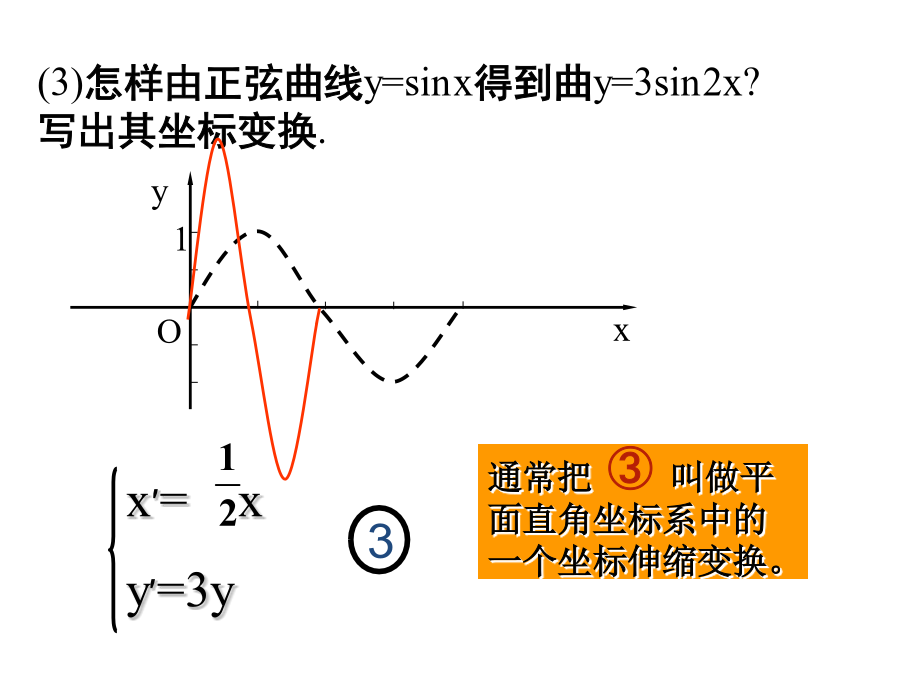
平面直角坐标系中------的伸缩变换xy=3sinx(3)怎样由正弦曲线y=sinx得到曲y=3sin2x?写出其坐标变换.定义:设P(x,y)是平面直角坐标系中任意一点,在变换注(1)(2)把图形看成点的运动轨迹,平面图形的伸缩变换可以用坐标伸缩变换得到;(3)在伸缩变换下,平面直角坐标系不变,在同一直角坐标系下进行伸缩变换。在平面直角坐标系中,求下列方程所对应的图形经过伸缩变换由上所述可以发现,在伸缩变换下,直线仍然变成直线,而圆可以变成椭圆。有关曲线伸缩变换的一般性结论①.直线经过伸缩变换后,仍是

11平面直角坐标系中的伸缩变换.ppt
平面直角坐标系中的伸缩变换解决轨迹应用题的关键:1、建立平面直角坐标系2、设点(点与坐标的对应)3、限制条件4、列式(方程与坐标的对应)5、化简建系时,根据几何特点选择适当的直角坐标系。平面直角坐标系中的伸缩变换定义:设P(x,y)是平面直角坐标系中任意一点,在变换注(1)(2)把图形看成点的运动轨迹,平面图形的伸缩变换可以用坐标伸缩变换得到;(3)在伸缩变换下,平面直角坐标系不变,在同一直角坐标系下进行伸缩变换。练习:1.在直角坐标系中,求下列方程所对应的图形经过伸缩变换2.在同一直角坐标系下,求满足下
