
齐次线性方程组解的结构.ppt

lj****88








亲,该文档总共20页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

齐次线性方程组解的结构.ppt
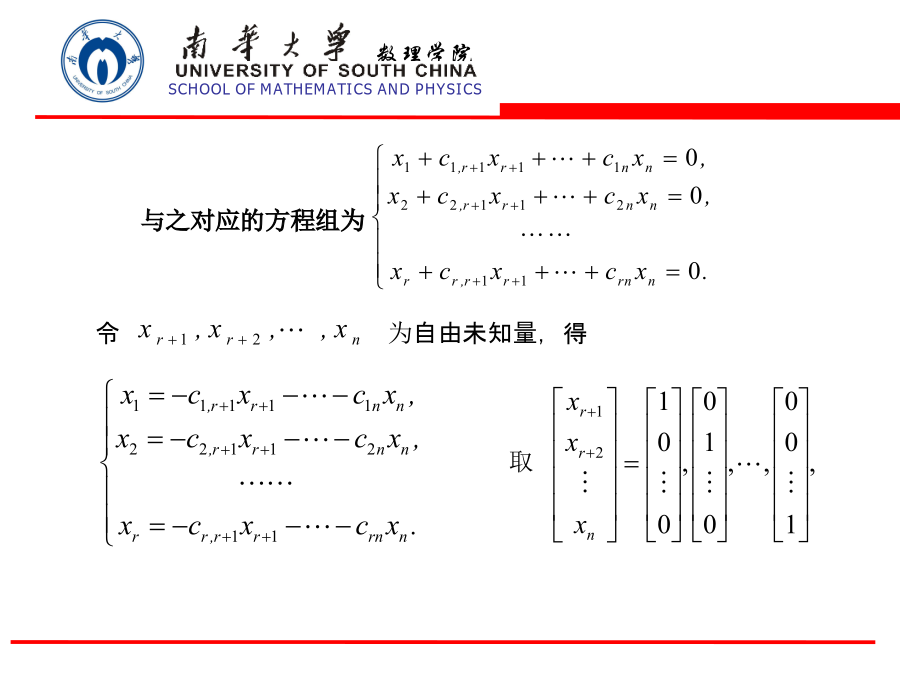
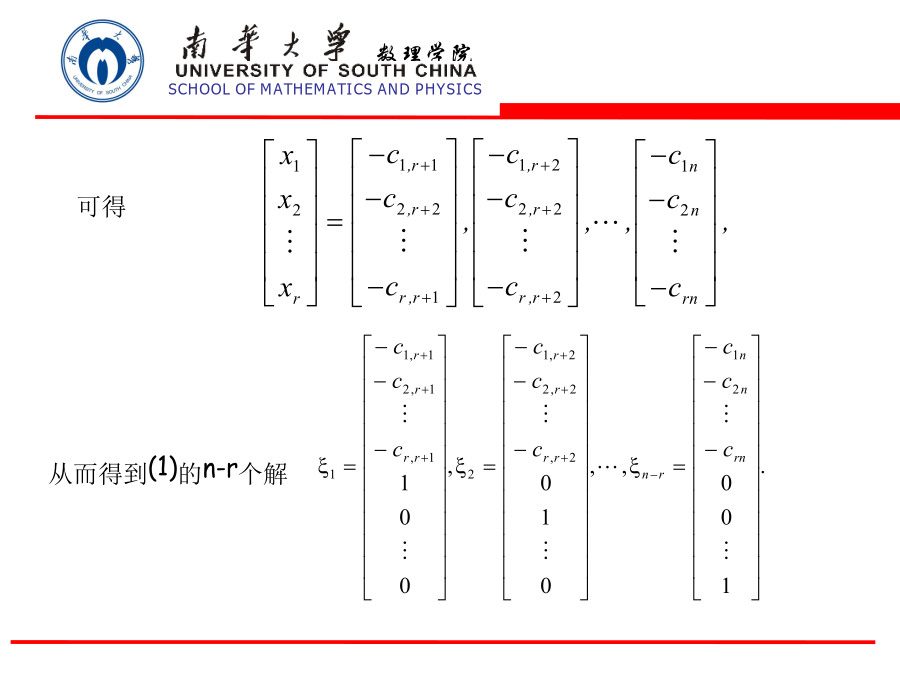
一、齐次线性方程组解的结构2解空间齐次线性方程组(1)一组解向量,证:代入自由未知量,事实上,若事实上,由是(1)的解,得5齐次线性方程组解的结构例1求齐次线性方程组的基础解系.令得附:写出方程组(1)的一般解:向量组即为方程组(1)的一个基础解系.二、一般线性方程组解的结构1解的性质2非齐次线性方程组解的结构求出(3)的导出组(4)的一个基础解系例2求解方程组由令,得

齐次线性方程组解的结构.ppt
1齐次线性方程组解的结构2非齐次线性方程组解的结构一、齐次线性方程组解的结构因此,求齐次线性方程组的解就是求出解空间,这就需要求出解空间的一组基。称解空间的一组基为方程组的基础解系。定理1齐次线性方程组若有非零解,则它一定有基础解系,且基础解系所含解向量的个数等于n-r,其中r是系数矩阵的秩。首先,这n-r个解向量显然线性无关.例1解齐次线性方程组秩r=2<4,故有非零解.二、非齐次线性方程组解的结构定理3(非齐次线性方程组解的结构定理)如果非齐次线性方程组有解,那么它的一个解与其导出方程组的解之和是非齐

齐次线性方程组解的结构.pptx
1.解向量的概念则上述方程组(1)可写成向量方程称为方程组(1)的解向量,它也就是向量方程(2)的解.2.齐次线性方程组解的性质(2)若为的解,为实数,则也是的解.1.基础解系的定义2.线性方程组基础解系的求法现对取下列组数:依次得下面证明是齐次线性方程组解空间的一个基.由于是的解故也是的解.所以是齐次线性方程组解空间的一个基.定理11例1求齐次线性方程组例2解线性方程组即方程组有无穷多解,所以原方程组的一个基础解系为

非齐次线性方程组的解结构.ppt
三、非齐次线性方程组的性质证明证明其中为对应齐次线性方程组的通解,为非齐次线性方程组的任意一个特解.3.与方程组有解等价的命题4.线性方程组的解法例1求解方程组由于所以方程组无解.例3.设线性方程组3)当b=3时,有1.齐次线性方程组基础解系的求法由于故为齐次线性方程组的一个基础解系.线性方程组

齐次线性方程组解的结构ppt课件.ppt
§6.2齐次线性方程组解的结构一.齐次线性方程组解的结构(1)若为的解,则2.基础解系定理4.6.2.当r(A)<n时,齐次线性方程组的基础解系含有n-r个解向量.得到方程组的一个基础解系为例1·求下面齐次线性方程组的一个基础解系。11故原方程组的通解为齐次线性方程组求全部解的图示:习题4.63(2)
