预览加载中，请您耐心等待几秒...

齐次线性方程组解的结构PPT课件.ppt

预览
1/10
2/10
3/10
4/10
5/10
6/10
7/10
8/10
9/10
10/10

亲，该文档总共22页，到这已经超出免费预览范围，如果喜欢就直接下载吧～

下载提示 文本预览

如果您无法下载资料，请参考说明：

1、部分资料下载需要金币，请确保您的账户上有足够的金币

2、已购买过的文档，再次下载不重复扣费

3、资料包下载后请先用软件解压，在使用对应软件打开

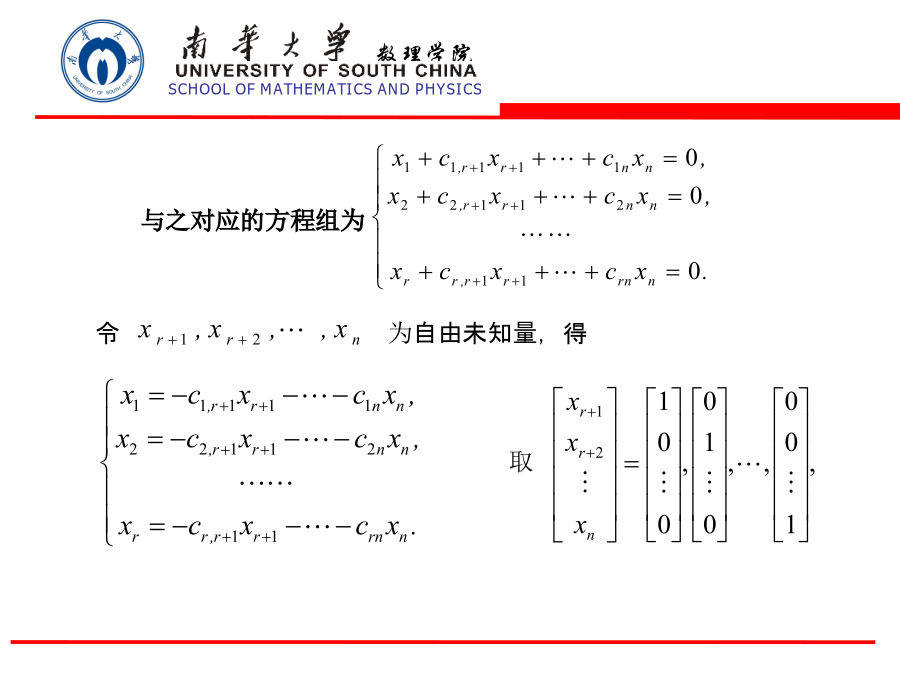
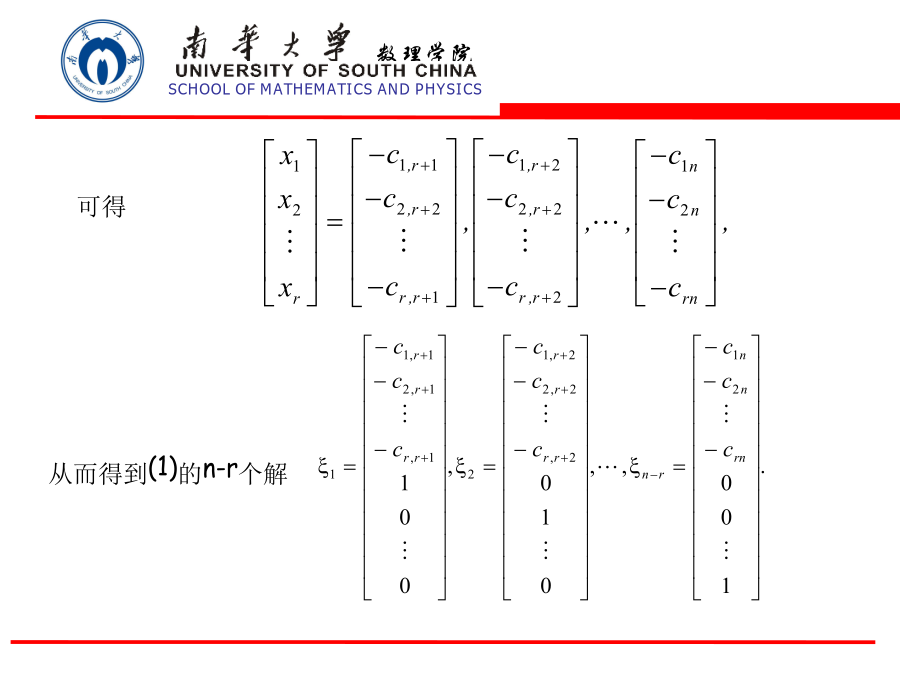
1齐次线性方程组解的结构 2非齐次线性方程组解的结构一、齐次线性方程组解的结构因此，求齐次线性方程组的解就是求出解空间，这就需要求出解空间的一组基。称解空间的一组基为方程组的基础解系。定理1齐次线性方程组若有非零解，则它一定有基础解系，且基础解系所含解向量的个数等于n-r，其中r是系数矩阵的秩。首先，这n-r个解向量显然线性无关.例1解齐次线性方程组秩r＝2<4，故有非零解.二、非齐次线性方程组解的结构定理3（非齐次线性方程组解的结构定理）如果非齐次线性方程组有 解，那么它的一个解与其导出方程组的解之和是非齐次线性方 程组的一个解，非齐次线性方程组的任意解都可以写成它的一 个特解与其导出方程组的解之和。其中为对应齐次线性方程组的通解，为非齐次线性方程组的任意一个特解.解对增广矩阵进行行初等行变换对应的齐次线性方程（去掉常数列）的基础解系为例3设线性方程组(2)当p=1，且1-4t+2pt=1-2t=0即t=时，方程组有无穷多解，此时练习.设２．齐次线性方程组解的情况