第9章-差错控制编码.ppt

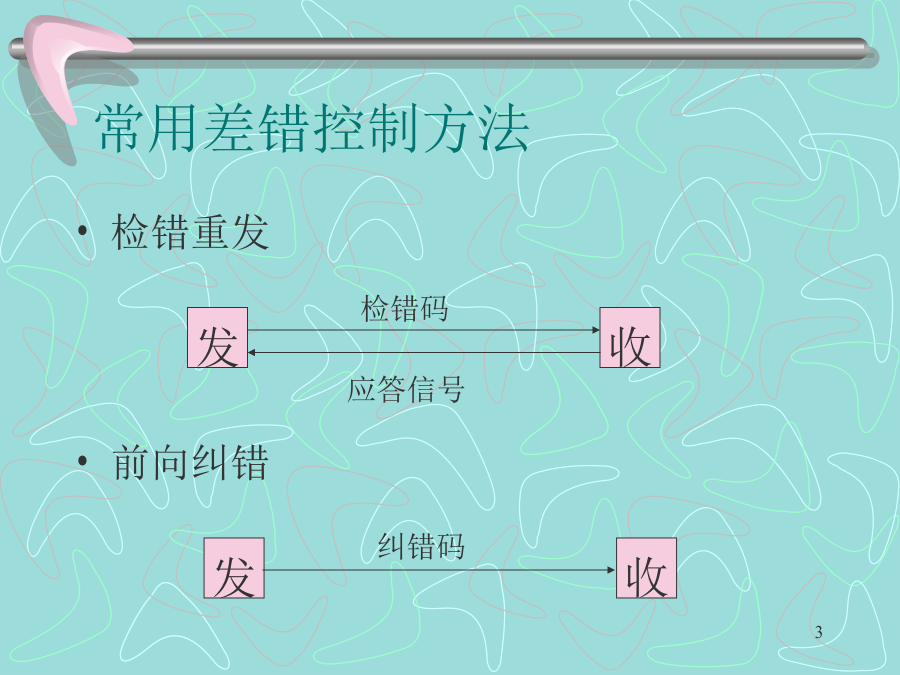
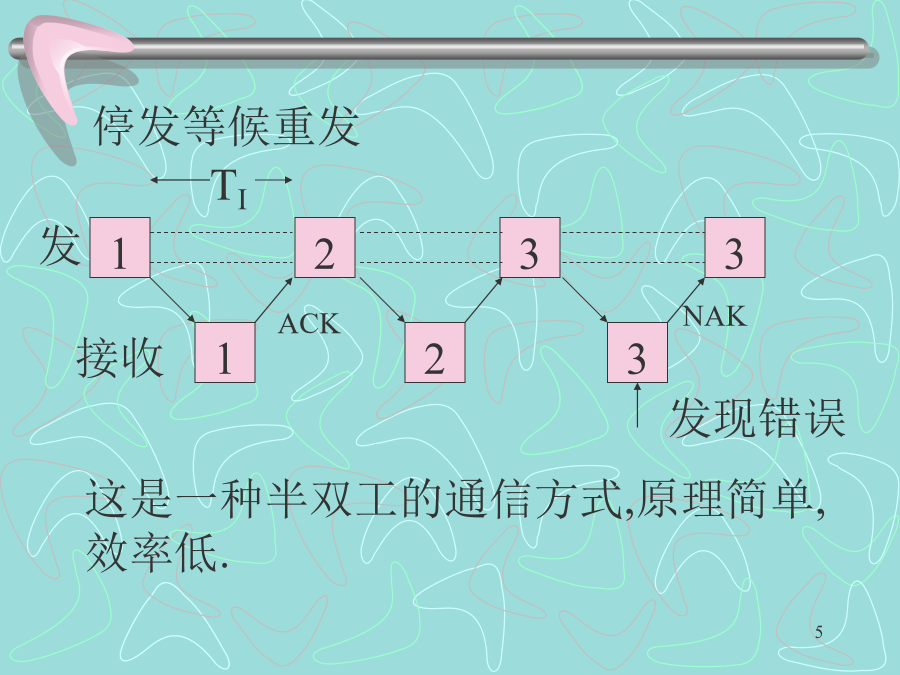
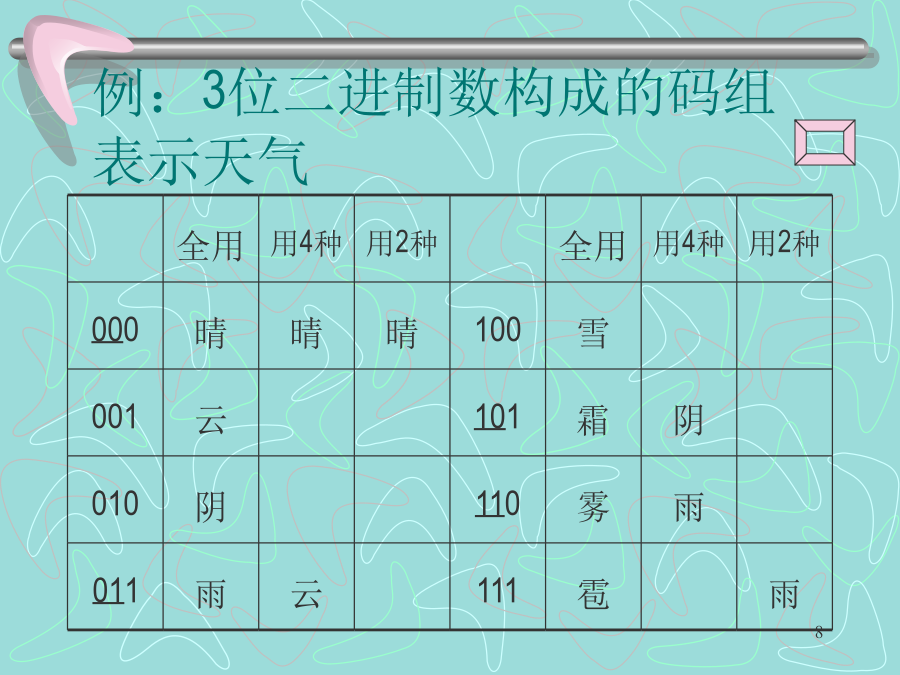
第9章差错控制编码9.1引言常用差错控制方法混合纠错
停发等候重发返回重发9.2纠错编码的基本原理例：3位二进制数构成的码组表示天气如不要检（纠）错，传输4种不同的信息，用两位码组就够了，这两位码代表所传信息，称为信息位，多增加的称为监督位。d0的大小直接关系着编码的检，纠错能力。A当n=7P=10-3时9.3常用的简单编码二维奇偶监督码恒比码9.4线性分组码奇偶监督码是一种最简单的线性码,偶校验时设分组码(n,k)中k=4,为纠正一位错码,要求r≥3,则n=k+r=7计算监督位编码速率=简记为或或具有形式的生成矩阵称为典型生成矩阵。发送码组A在传输过程中可能发生误码，设接收到的码组为B=[bn-1bn-2…b0]接收端计算校正子为例设且有3个接收码组解：1）若无错，则错误图样为0，S为0线性码的重要性质9.5循环码9.5.1循环码原理码多项式的按模运算若F(x)=N(x)Q(x)+R(x)在循环码中,若T(x)是一个长为n的许用码组,则xiT(x)在按模xn+1运算下,也是一个许用码组.在循环码中，一个（n，k）码有2k个不同码组g(x),xg(x),x2g(x),…xk-1g(x)都是码组,且线性无关,故循环码的生成矩阵G可写成所有码多项式T(x)都可被g(x)整除,而且,任一次数不大于k-1的多项式乘g(x)都是码多项式.故g(x)是xn+1的一个n–k次因式,此即寻找g(x)的方法.

例9.5.2循环码的编、解码方法编码步骤

监督位a循环码的解码9.6卷积码在编码器复杂性相同的情况下,卷积码的性能优于分组码.654321b6b5b4b3b2b1假定b1以前各码元均未发生错误,则(1)式经线性变换监督矩阵H假定b1进入编码器之前，各级移存器处于“0”状态
H1

H1：截短监督矩阵自第7行起，每行结构相同，只是每行的起始比上一行多两个“0”。In-k—n-k阶单位方阵Pi—（n-k）×k矩阵0—n-k阶全零方阵生成矩阵G基本生成矩阵gg=[IKQ10Q20Q3…0QN]卷积码的图解表示（3，1，3）卷积码的树状图（3，1，3）卷积码的网格图（3，1，3）卷积码的状态图在前述编码器中，若起始状态为a，输入序列为11010111，求输出序列和状态变化路径对于（n，k，N）卷积码的一般情况，有如下结论：1、字体安装与设置