
铁磁性磁性耦合机理.pptx

快乐****蜜蜂






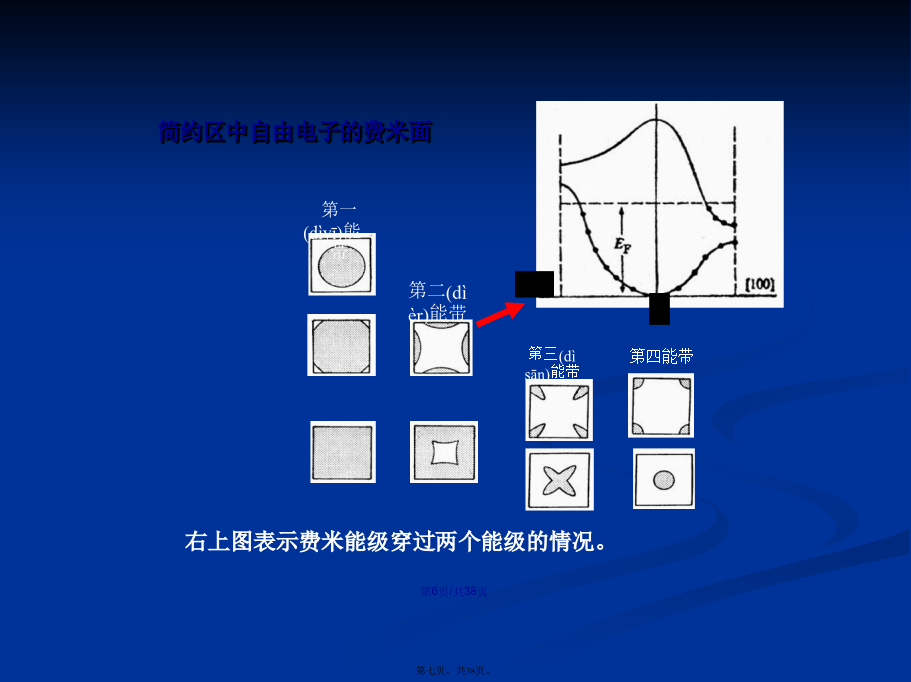

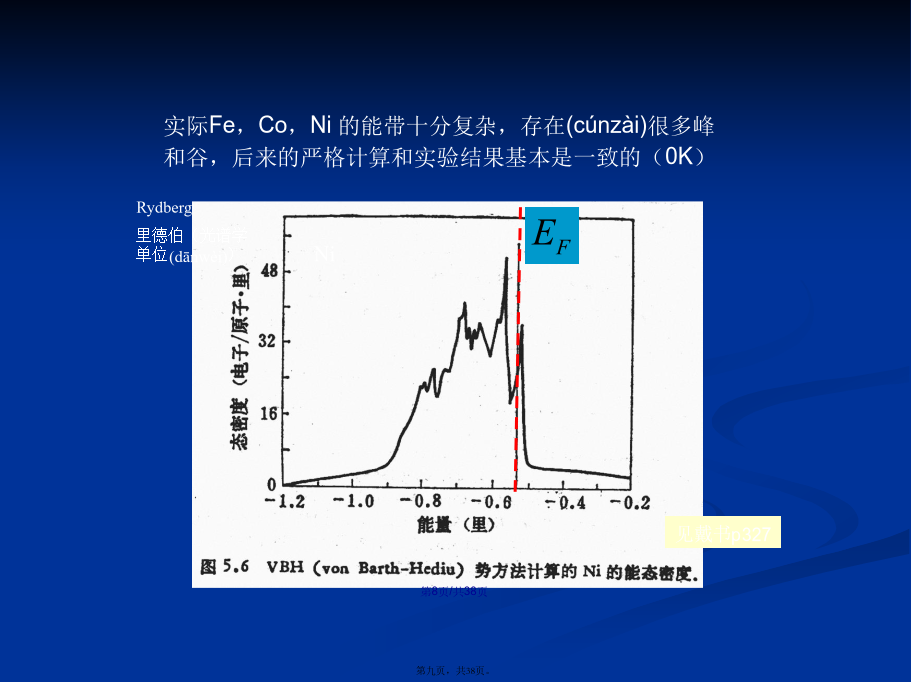

亲,该文档总共38页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

铁磁性磁性耦合机理.pptx
会计学问题的提出能带模型的物理图像能带论对铁磁性自发磁化的解释斯托纳判据巡游电子模型的发展金属铁磁性理论(lǐlùn)的发展现状实验表明由饱和磁化强度测量给出的Fe,Co,Ni原子磁距的平均有效玻尔磁子数分别(fēnbié)为2.2,1.7,0.6,有悖于局域电子模型给出的结论,数值不同且不是整数。按局域电子模型,与磁化率有关的居里常数应为:而由过渡金属磁化率测出的居里常数C无法给出整数或半整数自旋量子数S,且与饱和磁矩无关。在某些情况下有些金属的磁化率甚至不遵守居里-外斯定律。3.过渡族金属的结合能和电
铁磁性与反铁磁性.ppt
第12章铁磁性与反铁磁性目录物质物质磁性分类的原则1.铁磁序交换场近似地表示量子力学的交换作用假设i、j两原子,自旋Si,Sj,其相互作用能:U=-2JSi·Sj(J:交换积分)在平均场近似下,J与Tc的关系在平均场近似下,对于S=1/2,磁化强度与温度的函数关系为:低温下,平均场近似给出的磁化强度的偏离量:ΔM=M(0)-M(T)绝对零度下的饱和磁化强度:2s2金属Cu的4s带和3d带关系示意图2.磁波子磁波子的色散关系:长波近似下k2的系数一般可由中子散射或自旋波共振准确测定。3.中子散射4.亚铁磁序

铁磁性与反铁磁性.pptx
会计学物质磁性(cíxìng)分类的原则1.铁磁序交换场近似地表示量子力学的交换作用假设i、j两原子,自旋Si,Sj,其相互作用能:U=-2JSi·Sj(J:交换积分(jīfēn))在平均场近似下,J与Tc的关系在平均场近似(jìnsì)下,对于S=1/2,磁化强度与温度的函数关系为:低温下,平均场近似(jìnsì)给出的磁化强度的偏离量:ΔM=M(0)-M(T)绝对零度(juéduìlíngdù)下的饱和磁化强度:2s2金属(jīnshǔ)Cu的4s带和3d带关系示意图2.磁波子磁波子的色散关系:长波近

ZnO基稀磁半导体的铁磁性机理.docx
ZnO基稀磁半导体的铁磁性机理一、引言随着纳米材料科技的迅猛发展,研究人员发现微观结构对于材料性能的影响越来越明显。在磁性材料领域,磁性半导体备受关注,这类材料既拥有半导体的电学性质,也具备铁磁性。其中,ZnO基稀磁半导体因其特殊的晶体结构和化学组成,成为了磁性半导体研究的热点领域之一。本文将从ZnO基稀磁半导体的铁磁性机理入手,系统介绍该材料的结构及磁性特性,深入探究其铁磁相的来源和本质特点,并探讨其在磁存储领域的应用前景。二、ZnO基稀磁半导体的结构与磁性特性ZnO是一种具有六方密堆积晶体结构的物质,

铁磁物质由铁磁性转变为顺磁性的微观机理.doc
第一标段:物理学专业实验室(二)序号设备名称性能指标技术参数单位数量1高温居里点测试仪1.铁磁物质由铁磁性转变为顺磁性的微观机理;2.感应法测定铁磁物质居里温度的原理和方法;3.测定铁磁物质的居里温度。套22光纤马赫-曾德尔干涉仪1.熟悉光纤马赫-曾德尔干涉仪的工作原理,并通过自己搭建光路,掌握马赫-曾德尔干涉仪光路的调整方法。2.观察双光束干涉现象。3.将光纤分别用在压力、位移、温度场内,观察干涉条纹变化。台43热辐射与红外扫描成像装置红外转换器:输入端口通过专用双鼠标线与红外热辐射传感器相连,输出热辐
