§5.2 平面向量的数量积及平面向量的应用x.ppt

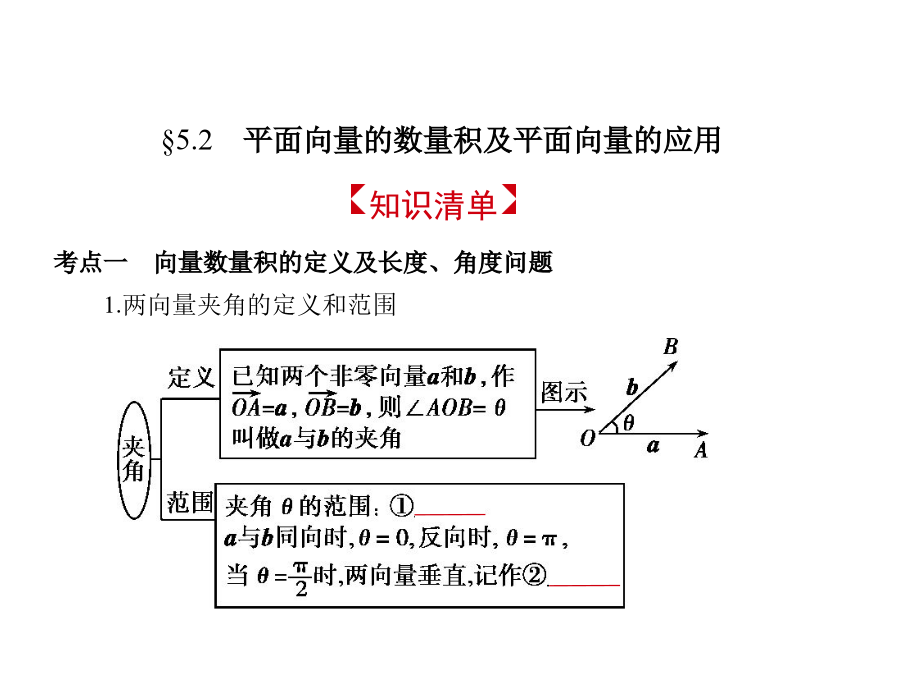
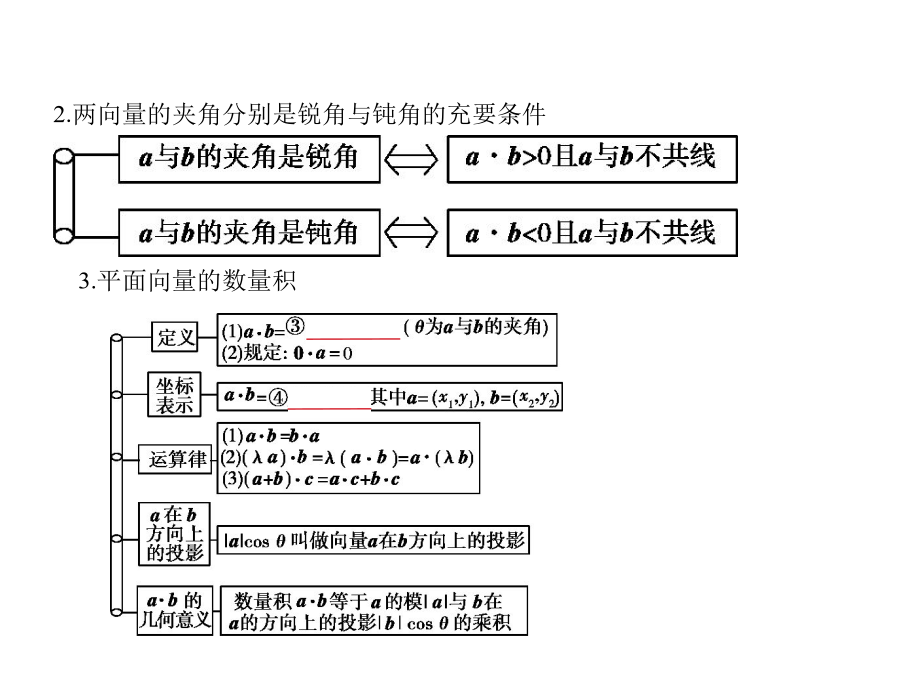
第五章平面向量§5.2平面向量的数量积及平面向量的应用2.两向量的夹角分别是锐角与钝角的充要条件4.向量数量积的性质
设a,b都是非零向量,e是与b方向相同的单位向量,θ是a与e的夹角,则
(1)e·a=a·e=⑤|a|·cosθ.
(2)a⊥b⇔⑥a·b=0.
(3)当a与b同向时,⑦a·b=|a||b|;当a与b反向时,⑧a·b=-|a||b|.
特别地,a·a=⑨|a|2.
(4)cosθ=  .
(5)|a·b|≤|a|·|b|.5.坐标表示
(1)若a=(x,y),则a·a=a2=|a|2=x2+y2,|a|=  .
(2)若A(x1,y1),B(x2,y2),则| |=  ,这就是平面内
两点间的距离公式.考点二利用向量解决平行、垂直问题
若两个非零向量a=(x1,y1),b=(x2,y2),则
(1)a⊥b⇔ x1x2+y1y2=0.
(2)a∥b⇔ x1y2-x2y1=0.
拓展延伸
向量中常用的结论:
在△ABC中,设∠A,∠B,∠C所对的边分别为a,b,c.
(1)在 =λ 的条件下,存在λ,使得I为△ABC的内心;
a +b +c =0⇔P为△ABC的内心.
(2)| |=| |=| |⇔P为△ABC的外心.(3) + + =0⇔G为△ABC的重心.
(4) · = · = · ⇔P为△ABC的垂心.
求平面向量模长的方法
1.把几何图形放到适当的坐标系中,写出有关向量的坐标,求向量的长度.如向量a=(x,y),求向量a的模长只需利用公式|a|= 即可.
2.若不把向量放到坐标系中研究,则求此类问题的通法是利用向量的运算法则及其几何意义或应用向量的数量积公式,关键是会把向量a的模进行如下转化:|a|= .
例1(2017河北“五个一名校”联盟模拟,4)已知向量a,b满足:|a|=2,|b|=4,<a,b>= ,则|3a-2b|= (B)
A.52B.2 C. D.2 解题导引
由题意求得a·b的值 利用|3a-2b|= 
求得结果解析建立平面直角坐标系如图所示,则A(2,0),

设P(0,y),C(0,b),则B(1,b),且0≤y≤b.
所以 +3 =(2,-y)+3(1,b-y)=(5,3b-4y),
所以| +3 |= (0≤y≤b),
所以当y= b时,| +3 |取最小值5.求平面向量夹角的方法
1.定义法:利用向量数量积的定义知,cosθ= ,其中两个向量的夹角θ
∈[0,π],求解时应求出三个量:a·b,|a|,|b|或找出这三个量之间的关系.
2.坐标法:若a=(x1,y1),b=(x2,y2),θ为a,b的夹角,则cosθ= .
3.三角函数法:可以把所求两向量的夹角放到三角形中,利用正、余弦定理和三角形的面积公式等内容进行求解.
例3(2015重庆,7,5分)已知非零向量a,b满足|b|=4|a|,且a⊥(2a+b),则a与b的夹角为 (C)
A. B. C. D. 解题导引
由a⊥(2a+b)得a·b
=-2|a|2 利用向量的夹角公式及
范围求出a与b的夹角
例4(2017江西七校联考,13)已知向量a=(1, ),b=(3,m),且b在a的方向
上的投影为-3,则向量a与b的夹角为.解析∵b在a的方向上的投影为-3,
∴|b|cos<a,b>=-3,
又|a|= =2,∴a·b=|a||b|cos<a,b>=-6,
又a·b=1×3+ m,∴3+ m=-6,解得m=-3 ,
∴b=(3,-3 ),∴|b|= =6,
∴cos<a,b>= = =- ,
∵0≤<a,b>≤π,∴a与b的夹角为 π.用向量法解决平面几何问题的方法
1.用向量法解决平面几何问题的基本步骤:①建立平面几何与向量的联系,用向量表示问题中涉及的几何元素,将平面几何问题转化为向量的问题;②通过向量运算,研究几何元素之间的关系,如距离、夹角等问题;③把运算结果转化成几何关系.
2.用向量法解平面几何问题,主要是通过建立平面直角坐标系将问题坐标化,然后利用平面向量的坐标运算求解有关问题,这样可以避免繁杂的逻辑推理,同时加强了数形结合思想在解题中的应用.
例5(2016天津,7,5分)已知△ABC是边长为1的等边三角形,点D,E分别是边AB,BC的中点,连接DE并延长到点F,使得DE=2EF,则 · 的值为
 (B)解题导引
解法一:用 和 表示向量 →求 · 
解法二:建立平面直角坐标系→求出相关点的坐标→求出 与 的坐
标→求 · 
解析解法一:如图,

 · =( + )· = · 
= · 
= · 
= · =-  · +  
=- ×1×1×cos60°+ ×12= ,故选B.
解法二:建立平面直角坐标系,如图.

则B ,C ,A ,所以 =(1,0).
易知DE= AC,则EF= AC= ,因